 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Швидкість матеріальної точки
Для характеристики руху матеріальної точки використовується векторна величина - швидкість, яка визначає як стрімкість руху, так і його напрямок в даний момент часу. Нехай у момент часу t положення точки визначається радіусом-вектором r. За проміжок часу Dt точка пройде шлях DS та отримає переміщення Середньою швидкістю ` Межа середньої швидкості матеріальної точки за умови, що час Dt ® 0, дорівнює її миттєвій швидкості V:
Таким чином, миттєва швидкість дорівнює першій похідній від радіуса-вектора за часом.
Через те, що при Dt ® 0, модуль радіуса-вектора матеріальної точки практично дорівнює довжині шляху, модуль вектора миттєвої швидкості буде дорівнювати:
Тобто модуль миттєвої швидкості дорівнює першій похідній від шляху за часом. Вектор швидкості
Знаючи модуль вектора миттєвої швидкості в кожний момент часу, можна обчислити шлях, який пройшла матеріальна точка за деякий проміжок часу у випадку, коли її швидкість не залишається постійною, а змінюється з часом. Для цього з виразу (1.8) маємо: dS = V(t) dt , Інтегруємо цей вираз у границях від t1 до t2 та отримаємо:
У випадку рівномірного руху матеріальної точки, тобто коли V = const, з вище наведеного виразу отримаємо:
Отриманий вираз добре знайомий з елементарної кінематики. У міжнародній системі СІ швидкість руху має таку розмірність: [v] = [r / t] = [м×с-1].
Для характеристики зміни швидкості руху матеріальної точки з часом, як за модулем так і за напрямком, використовується вектор прискорення. Розглянемо рух матеріальної точки по довільній траєкторії (див. рис. 1.4). Припустимо, що за час Dt точка перемістилася з положення А в положення В, пройшовши шлях DS. При цьому швидкість її руху зросла з Середнім прискоренням називається векторна величина, що дорівнює відношенню зміни швидкості
Миттєвим прискоренням матеріальної точки є вектор, що дорівнює межі середнього прискорення за умови, що Dt ® 0:
Тоді з урахуванням виразу (1.7) отримаємо:
Таким чином, миттєве прискорення матеріальної точки дорівнює першій похідній від вектора швидкості, або другій похідній від радіуса-вектора за часом.
 так, щоб його початок співпав з початком вектора так, щоб його початок співпав з початком вектора  . Різницю цих векторів, тобто вектор . Різницю цих векторів, тобто вектор  , розкладемо на дві складові: , розкладемо на дві складові:  та та 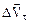 (див. рис. 1.4). З цього рисунка видно, що вектор (див. рис. 1.4). З цього рисунка видно, що вектор  несе відповідальність за зміну швидкості за напрямком, а вектор несе відповідальність за зміну швидкості за напрямком, а вектор 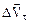 - за зміну вектора швидкості за її модулем. - за зміну вектора швидкості за її модулем.
Межа відношення модуля вектора
Тобто тангенціальне прискорення дорівнює першій похідній від швидкості матеріальної точки за часом. Зробимо більш детальний аналіз геометричної схеми, яка наведена на рис. 1.4. З подібності трикутників АВО і АСД, довести яку пропонується читачам самостійно, маємо: АВ/R = DVn/V1. Враховуючи, що за умови Dt ® 0, АВ = V Dt, отримаємо:
де R - радіус кривизни траєкторії у даній точці. Межа відношення модуля вектора DVn до проміжку часу Dt, за який він змінився, за умови, що Dt ® 0, отримала назву нормальне прискорення аn. При Dt ® 0 V1 ® V, а значить:
Вважаючи на те, що точки А і В (рис. 1.4) за умови Dt ® 0, будуть на дуже малій відстані одна від одної, можна довести, що
Величина, обернена радіусу кривизни траєкторії руху матеріальної точки, називається кривизною цієї траєкторії. Вектор повного прискорення та його модуль знаходять за такими формулами:
А тепер ще раз підкреслимо, що тангенціальна складова прискорення характеризує зміну швидкості за модулем, а нормальна - зміну швидкості за напрямком. Розмірність прискорення у системі СІ: [a] = [V / t] = [м с-2].
Поиск по сайту: |
 (див. рис. 1.3).
(див. рис. 1.3). матеріальної точки називається відношення вектора її переміщення
матеріальної точки називається відношення вектора її переміщення  , (1.6)
, (1.6) , (1.7)
, (1.7) Рис. 1.4.
Рис. 1.4.
 , (1.8)
, (1.8) , (1.9)
, (1.9)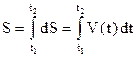 , (1.10)
, (1.10) , (1.11)
, (1.11) до
до 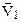 , тобто на
, тобто на  .
. , (1.12)
, (1.12) , (1.13)
, (1.13) , (1.14)
, (1.14) , (1.16)
, (1.16) Þ
Þ 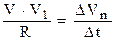 ,
, , (1.17)
, (1.17)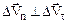 . А це у свою чергу означає взаємну перпендикулярність нормального та тангенціального прискорення.
. А це у свою чергу означає взаємну перпендикулярність нормального та тангенціального прискорення.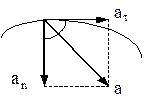 Рис. 1.5.
Рис. 1.5.
 , (1.18)
, (1.18)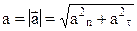 , (1.19)
, (1.19)