 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Системи відліку. Траєкторія. Шлях і переміщенняСтр 1 из 3Следующая ⇒
Конспект Лекцій ЧАСТИНА ПЕРША КЛАСИЧНА МеханікА Класична механіка є складовою частиною загальної фізики і вивчає найпростішу форму руху матерії - механічний рух, який являє собою зміну взаємного розташування тіл або їх частин. Розвиток механіки як науки почався з III століття до нашої ери, коли видатний вчений Архімед (287-212 до н.е.) сформулював закон рівноваги важеля та закон рівноваги плаваючих тіл. Основні закони механіки виявлені Г.Галілеєм (1564-1642) та остаточно сформульовані І.Ньютоном (1643-1727). Механіка Галілея - Ньютона вивчає закони руху макроскопічних тіл, швидкість яких незначна у порівнянні зі швидкістю світла. Закони руху макроскопічних тіл з швидкістю, яку можна порівняти зі швидкістю світла, вивчається у рамках релятивістської механіки, основні принципи якої були сформульовані А.Ейнштейном (1879-1955). Для опису руху мікроскопічних тіл (окремі атоми, елементарні частинки) працею цілого ряду видатних фізиків XX сторіччя розроблена квантова механіка.
У механіці (за винятком релятивістської механіки) ми будемо вивчати рух макроскопічних тіл, швидкість яких незначна у порівнянні з швидкістю світла. При цьому простір і час ми будемо розглядати як об’єктивні форми буття матерії, однак відокремлені один від одного та від руху матеріальних тіл. У подальшому ми обмежимось вивченням двох основних розділів механіки: кінематики і динаміки. Кінематика - вивчає закони, які описують механічний рух матеріальних тіл незалежно від причин, що викликали цей рух. Динаміка - вивчає закони, які описують механічний рух матеріальних тіл та ті причини, що викликали або змінили цей рух.
КІНЕМАТИКА матеріальної точки Системи відліку. Траєкторія. Шлях і переміщення. Усі тіла, що нас оточують, складаються з величезної кількості атомів і молекул, які в комплексі являють собою макроскопічні системи. Механічні властивості таких систем визначаються їх хімічним складом, внутрішньою будовою і структурою, вивчення яких виходить далеко за рамки механіки. Тому для опису стану макроскопічних тіл в механіці користуються спрощеними моделями, застосування яких значно полегшує розв’язання конкретних фізичних задач. Головними з них є моделі матеріальної точки та абсолютно твердого тіла. Матеріальною точкою називають тіло деякої маси, форма та розміри якого несуттєві в умовах конкретної задачі. Абсолютно твердим тілом називають тіло, відстань між будь-якими двома його точками завжди залишається незмінною. Положення деякого тіла у просторі може бути визначене тільки по відношенню до другого довільно визначеного тіла, яке отримало назву тіла відліку. Умовно нерухоме тіло відліку та жорстко зв'язана з ним довільна система координат, яка забезпечена годинником, називається системою відліку. У класичній механіці найбільш часто використовують прямокутні (декартові) системи координат (див. рис. 1.1). Положення точки А у декартовій системі координат можна задати двома еквівалентними засобами: або вказати значення трьох координат x, y, z точки А, або вказати радіус-вектор
Модуль радіус-вектора дорівнює:
Кількість незалежних координат, які повністю визначають положення матеріальної точки у просторі, називається числом степенів вільності. Наприклад, якщо точка рухається у просторі, то вона має три степені вільності (координати x, y, z), якщо вона рухається по поверхні, то має два степені вільності (координати x, y), а якщо вона рухається по деякій лінії, то має один степінь вільності (координата x).
Траєкторією називається лінія, яку описує матеріальна точка в просторі при її русі відносно вибраної системи відліку. У залежності від форми траєкторії рух може бути прямолінійним або криволінійним. Якщо з рівнянь (1.2) виключити час t, то неважко отримати рівняння траєкторії руху матеріальної точки. Довжина шляху DS - це скалярна величина, що дорівнює частині траєкторії, яку пройшла точка за вибраний проміжок часу. Розглянемо рух матеріальної точки по довільній траєкторії (рис. 1.2). Нехай матеріальна точка рухається по криволінійній траєкторії так, що в момент часу t = t1 вона знаходилась в точці А
Вектор, проведений з початкового положення точки у положення, яке вона займає у даний момент часу, отримав назву вектора переміщення
З малюнка на рис. 1.2 зрозуміло, що довжина шляху матеріальної точки завжди перевищує модуль її вектора переміщення:
Знак рівності у формулі (1.5) має місце при прямолінійному русі матеріальної точки.
Поиск по сайту: |
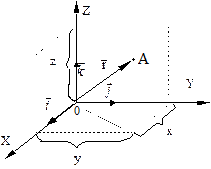 Рис. 1.1.
Рис. 1.1.
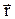 цієї точки.
цієї точки.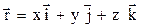 , (1.1)
, (1.1)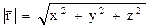 ,
,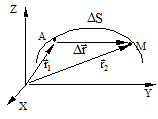 Рис. 1.2.
Рис. 1.2.
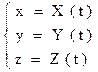 , (1.2)
, (1.2)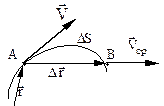 Рис. 1.3.
Рис. 1.3.
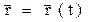 , (1.3)
, (1.3)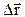 .
.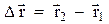 , (1.4)
, (1.4) , (1.5)
, (1.5)