 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема Коши о конечных приращениях
С фамилиями Неравенство Бернулли: Если
Бином Ньютона: формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид:
Лемма Больцана-Вейерштрасса Из всякой ограниченной числовой последовательности можно выделить сходящуюся подпоследовательность. Из этой леммы вытекает, что всякая ограниченная числовая последовательность имеет хотя бы одну предельную точку.
Теорема (Критерий Коши) Для того чтобы числовая последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной Фундаментальная последовательность, или сходящаяся в себе последовательность, или последовательность Коши — последовательность точек метрического пространства такая, что для любого заданного расстояния существует элемент последовательности, начиная с которого все элементы последовательности находятся друг от друга на расстоянии не более чем заданное. Предел числовой последовательности по Гейне:
Вопрос о пределе функции сводится к вопросу о пределе двух числовых последовательностей.
Принцип сходимости (критерий Коши) для функции. Т. Для того, чтобы предельное значение функции f при если
если (1) (2) : Больцано-Коши (Теорема о промежуточных значениях)
Если функция
Первая теорема Вейерштрасса (Теорема о глобальной ограниченности)
Вторая теорема Вейерштрасса (Теорема о достижении наименьших и наибольших значений)
Если Теорема Кантора – это достаточные условия при которых равномерная функция является равномерно непрерывной. Если функция
Лемма Гейне-Бореля Из всякой бесконечной системы интервалов, покрывающей отрезок числовой прямой, можно выбрать конечную подсистему, также покрывающую этот отрезок. ФормулаЛейбница Формула Лейбница для n-ой производной произведения двух функций — обобщение правила дифференцирования произведения (и отношения) двух функций на случай n-кратного дифференцирования. Пусть функции f(z) и g(z) — n раз дифференцируемые функции, тогда
Теорема Тейлора. Если функция
Правило Лопиталя. Условия: 1. 2. g(x) и f(x) дифференцируемы в 3. 4. тогда Теорема Ферма Если функция f во внутренней точке x0∈Д имеет локальный экстремум и дифференцируема в ней, то f′(x0)=0. Точка x называется внутренней точкой множества Д, если она вxодит в это множество с некоторой своей окрестностью. Теорема Ролля Если функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю. Теорема Лагра́нжа если функция f непрерывна на отрезке [a;b] идифференцируема в интервале (a;b), то найдётся такая точка
Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка. Теорема Коши о конечных приращениях Если f, g непрерывны на [a,b], дифференцируемы на (a,b), то существует xÎ(a,b): g¢(x)(f(b) - f(a)) = f¢(x)(g(b) - g(a)).
Поиск по сайту: |
 , то:
, то: , для всех
, для всех 
 , где
, где 


 Какую бы последовательность
Какую бы последовательность  не пробегала независимая переменная
не пробегала независимая переменная  соответствующая последовательность значений функции стремится к
соответствующая последовательность значений функции стремится к Предел числовой последовательности на языке
Предел числовой последовательности на языке  ", по Коши
", по Коши существовало, необходимо и достаточно, в случае,
существовало, необходимо и достаточно, в случае, числа, выполнялось условие:
числа, выполнялось условие: (*)
(*)


 непрерывна на некотором промежутке и в двух точках этого промежутка
непрерывна на некотором промежутке и в двух точках этого промежутка 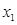 и
и  принимает не равные значения, то она принимает и все значения заключенные между ними. Для определенности положим, что
принимает не равные значения, то она принимает и все значения заключенные между ними. Для определенности положим, что 



 , то она достигает на этом отрезке свое наименьшее и наибольшее значение. Это означает, что
, то она достигает на этом отрезке свое наименьшее и наибольшее значение. Это означает, что 
 , т.е непрерывна на ограниченном, замкнутом множестве, то она равномерно непрерывна на этом множестве. Другими словами, если функция непрерывна на компакте, то она равномерно непрерывна на этом компакте.
, т.е непрерывна на ограниченном, замкнутом множестве, то она равномерно непрерывна на этом множестве. Другими словами, если функция непрерывна на компакте, то она равномерно непрерывна на этом компакте. где
где 
 имеет в некоторой окрестности точки a производную
имеет в некоторой окрестности точки a производную  порядка,
порядка,  то между точками a и x найдется точка ¥, такая что:
то между точками a и x найдется точка ¥, такая что: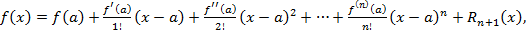 где
где


 или
или  ;
; (a);
(a); в
в  ,
, .
. , что
, что .
.