 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задача экономического содержания.⇐ ПредыдущаяСтр 35 из 35
С двух заводов поставляются автомобили для двух автохозяйств, потребности которых соответственно 200 и 300 машин. Первый завод выпустил 350 машин, второй – 150. Известны затраты на перевозку машин с завода в каждое автохозяйство.
Минимальные затраты на перевозку равны 7950 ден. ед. Найти оптимальный план перевозки машин так, чтобы общая стоимость транспортных расходов была бы наименьшей. В таблице указаны затраты на перевозку одной машины [21, с.55]. Эта задача уже рассматривалась в параграфе «оптимизационные модели». Здесь приводится решение без использования уравнений. Исключим информацию о минимальных затратах, составляющих 7950 ден. ед., и найдем оптимальный план перевозки машин так, чтобы общая стоимость транспортных расходов была бы наименьшей. Обозначим через В заключение этого параграфа подчеркнем, что, удаляя лишнее из условий задач, мы получаем более совершенные их формулировки и решения. Говорят, что знаменитый скульптор Роден на вопрос, как ему удается делать свои замечательные статуи, ответил: «Я беру глыбу мрамора и отсекаю от нее всё лишнее». Пожалуй, и не будет более подходящего случая, чтобы вспомнить эти слова, решая задачи, условия которых содержат лишнюю информацию.
Я слышу, и я забываю. Я вижу, и я запоминаю. Я делаю, и я понимаю. Китайская пословица ВАРИАНТ РАСЧЕТНО - ГРАФИЧЕСКОЙ РАБОТЫ Предлагаемая работа связана с проблемой оптимизации, часто возникающей во многих сферах человеческой деятельности. Наиболее простыми задачами оптимизации являются такие, которые сводятся к отысканию наименьшего или наибольшего значения функции, называемой целевой или критерием качества. Примеры задач такого рода рассмотрены нами ранее. В более сложных задачах необходимо сразу преследовать несколько целей. Например, если требуется установить оптимальные размеры бака объёмом Действительно, если известна стоимость 1 м2 листового железа и стоимость 1 м сварного шва (в них соответствующим образом учтены стоимости всех дополнительных видов работ), то задача будет сведена к минимизации одной целевой функции: стоимости изготовления бака. После такого предварительного обсуждения задачи мы можем описать её содержательную модель в виде текста: Из листового железа стандартной толщины требуется изготовить закрытый бак заданного объема Стоимость сварки одного метра шва – Определить радиус основания При этом необходимо: 1) составить математическую модель; 2) построить на ее основе вычислительный алгоритм или воспользоваться стандартным; 3) разработать программу или воспользоваться стандартной; 4) провести расчеты на ЭВМ, включая и необходимые для исследования устойчивости решений и оценки их точности; 5) проанализировать результаты расчетов и сделать выводы; 6) определить размеры бака так, чтобы минимальной была только стоимость железа; 7) определить размеры бака так, чтобы минимальной была только стоимость сварных швов; 8) используя результаты решения трех задач убедиться в справедливости основной теоремы системного анализа: "Если какая-либо система состоит из нескольких, связанных между собой подсистем, то оптимум всей системы не определяется оптимумом каждой из подсистем".
Решение. 1. Для построения математической модели обозначим радиус основания цилиндра через площадь полной поверхности общая длина швов стоимость изготовления бака –
Теперь математическая модель задачи может быть описана так: требуется найти такие 2. Учитывая, что целевая функция унимодальная, и так как вторая производная Это означает, что найдётся такой отрезок [ Конечно, для определения точки минимума можно было найти производную, приравнять её к нулю и решать полученное уравнение, например с помощью алгоритма половинного деления. 3. На этом этапе по соответствующему алгоритму составляется программа вычисления 4. Приведем таблицу 23.1 значений функции b = 30, V = 0,25, начиная со значения
Таблица 23.1– значений
Из таблицы 23.1 следует:
Таблица 23.2 – значений
Из таблицы 23.2 следует: С точностью до 0,01 можно принять Теперь найдем производную В этой связи отметим, что задача нахождения безусловного минимума (или экстремума) целевой функции несколько отличается от задачи нахождения точки минимума (экстремума). Дело в том, что в точке минимума функции производная равна нулю и потому малая погрешность при определении точки минимума или (экстремума) влечёт за собой погрешность второго порядка малости для минимума функции. «Таким образом, если цель исследования состоит лишь в том, чтобы придать функции
Рисунок 23.1 – График функции рисунке запись вида 1,2Е2 на оси ординат означает число
5. С помощью расчетов легко убедиться в том, что при
Рисунок 23.2 – График, поясняющий устойчивость значения
Проведенный анализ 6. Определение размеров бака по критерию минимума стоимости железа. Чтобы найти оптимальное для этого случая значение радиуса основания бака достаточно минимизировать функцию Очевидно также, что указанный критерий равносилен минимуму площади полной поверхности бака. Математическая модель такой задачи нами была построена в §7, где решение получено в виде формул: График площади полной поверхности
Рисунок 23.3– Верхний график выражает зависимость длины швов от радиуса, нижний – зависимость площади полной поверхности бака от радиуса 7. Определение размеров бака по критерию минимума стоимости сварных швов. Чтобы найти оптимальное для этого случая значение радиуса основания бака достаточно минимизировать функцию Очевидно также, что указанный критерий равносилен минимуму суммарной длины сварных швов. Обозначим радиус основания цилиндра через
Отсюда Таким образом, мы пришли к следующей математической модели: найти такое Так как При найденном Если по формулам График суммарной длины швов Главную (общую) задачу, сформулированную в § 23, можно рассматривать как систему, состоящую из двух подсистем (подзадач) указанных в пунктах 6) и 7). Так как 0,23 < 0,28 < 034, то результаты решения трех задач подтверждают справедливость основной теоремы: "Если какая-то система состоит из нескольких, взаимодействующих (связанных) между собой подсистем, то оптимум (наилучшие условия) для всей системы не определяется оптимумом для каждой из подсистем". А вот как иллюстрирует сущность этой теоремы с помощью простого мысленного эксперимента Ю. Поспелов в статье «Пока что взгляд не дальше «хуторка» (Газета «Правда» от 19 сентября 1990 г). «Пусть мы имеем два одинаково заряженных шарика и конусообразную чашку. Если в чашку положить один шарик, то он упадет на самое дно. Но если в чашку опустить сразу два шарика, то они, отталкиваясь, друг от друга, не могут одновременно занять положение на дне чашки: они немного поднимутся, что, конечно, не отвечает оптимальному положению для каждого шарика в отдельности. Эта важнейшая теорема системного анализа носит настолько общий характер, что приложима ко многим практическим (и часто практически важным) проблемам, а забвение ее ведет к неправильным выводам и решениям. Нельзя брать обособленно от других, какую - то одну подсистему и оптимизировать ее, надеясь получить наилучшее решение для этой подсистемы. Часто бывает просто обидно за честных и добросовестных людей, оптимизирующих какой-то отдельно взятый «хуторок», а потом удивляющихся, что ничего хорошего из их благих побуждений не получилось».
ЗАКЛЮЧЕНИЕ Итак, краткое обсуждение роли и назначения математических моделей в современной науке и технике завершено. Наше изложение существенно опиралось на знания, полученные при изучении математики в школе и вузе. Мы не могли не почувствовать той большой роли, которую выполняет математика при построении и исследовании математических моделей объектов в самом широком смысле. Именно математическая модель является инструментом, позволяющим превратить задачу практики в математическую задачу, при решении которой может использоваться аппарат математики в сочетании с вычислительной техникой. Однако, как отмечал академик Крылов А.Н., встречались представители техники, которые недооценивали значения математики. Они ссылались на то, что, например, «в средние века и в древности возводились неподражаемые дворцы и храмы, поражающие не только размерами, красотою форм и линий, но и легкостью сооружения, разумным использованием материала, соблюдением даже в деталях, например в контрфорсах, истинных принципов строительной механики, которой тогда не было, да и быть не могло, так как даже правило параллелограмма сил известно не было». Это давало возможность противникам математики высказать мнение, что она, в сущности, есть переливание из пустого в порожнее, ибо «всё, что в ней есть, взято из ее основных, до тривиальности очевидных, аксиом; значит, всеобъемлющий ум видел бы сразу в этих аксиомах и все их следствия, т.е. – всю математику». На это А.Н. Крылов отвечает: «Да, ум всеобъемлющий это видел бы, но известно, что ум человеческий ограничен – глупость беспредельна. Математика и нужна уму ограниченному, как подспорье для правильных умозаключений» (А.Н. Крылов Прикладная математика и ее значение для техники. М.: Изд-во АН СССР, 1931). Рассматривая вопросы применения математики к решению прикладных задач, укажем, что выдача результатов связана с моральной, материальной или юридической ответственностью. Поэтому на всех этапах (особенно на заключительном) математического моделирования с целью предотвращения ошибок необходимо использовать все возможные методы контроля. И именно поэтому проверке решений учебных задач необходимо уделять большое внимание. Подтвердим этот тезис решением математической и химической задач. Существует ли такое двузначное число, которое при делении на сумму квадратов его цифр даёт в частном 2 и в остатке 6, а при делении на произведение его цифр даёт в частном 4 и остатке 6?.
Её решение приводится в пособии [17, с. 280]. Рассмотрим его.
Проанализируем решение. В нем правильно применены формулы и все преобразования не вызывают возражений, а ответ ошибочный. Дело в том, что «математика - не формулы, как музыка - не ноты».По существу в представленном решении используется хорошо известная технология исследования: выдвигается гипотеза (предположение) (в нашем случае – искомое число существует), а затем гипотеза проверяется. В приведенном решении проверки нет. Но проверка показывает: деление числа 22 на произведение его цифр, т.е. на 4, даёт в частном 5 (а не 4) да и в остатке 2 (а не 6). Значит, «ответ 22» – ошибочный, а в учебнике [24, с. 230] он даже усилен: Существует; 22. Проверка результата – это один из элементов фундаментального исследования! Но, проверка еще и показала, что более совершенным содержанием этой задачи является формулировка: Существует ли такое двузначное число, которое при делении на произведение его цифр даёт в частном 4 и остатке 6? (остальная информация исключена). Этот результат опубликован в статье [Хрусталев А.Ф. К решению задачи 1151. Математика в школе, 1996, № 4]. Именно постановка задачи по-новому часто проливает свет на её подлинное содержание, которое в нашем случае будет таким: Существует ли такое двузначное число, которое при делении на произведение его цифр даёт в частном 4? Ответ: не существует. Действительно, на основании полного перебора всех двузначных чисел от 10 до 99, с проверкой каждого на выполнение условия: «Двузначное число при делении на произведение его цифр даёт в частном 4» придем к выводу, что число, о котором идет речь в задаче, не существует. Рассмотрим также другое решение, позволяющее существенно сократить перебор указанных чисел. Обозначив, через (10х+у)/(ху) = 4, (1) где
Из уравнения (1) следует х = у/(4у-10) (2) и у равно 2; 4; 6 или 8. Проверка показывает, что при указанных значениях у, х не является натуральным числом. Следовательно, двузначное число, о котором идет речь в задаче не существует. Существенно сократить количество опытов (с 90 до 4) по проверке каждого двузначного числа на выполнение указанного выше условия помогли знания из математики. Именно такая мысль нашла отражение в поэме А. С. Пушкина "Борис Годунов": "Учись мой сын: наука сокращает нам опыты быстротекущей жизни... " Итак, при решении этой задачи мы провели простейшие вычислительные эксперименты, включающие в себя элементы современной технологии и методологии научных исследований. Конечно, можно привести и более изящное решение переформулированной задачи. Ведь уравнение (1) равносильно (4х – 1)(2у-5) =5∙1 (3) и Эта задача эквивалентная первоначальной, является наилучшей и даже оптимальной, поскольку её формулировка, содержит только одно количественное данное «4», которое естественно удалить нельзя. А по словам Экзюпери «Совершенство достигается не тогда, когда нечего прибавить, но когда уже ничего нельзя отнять».Новейшая формулировка задачи отражает „Концепцию развития математического образования в РФ”, утвержденную председателем правительства Дмитрием Медведевым 24 декабря 2013 года, в которой указано, что математическое образование должно «обеспечивать каждого обучающегося развивающей интеллектуальной деятельностью на доступном уровне, используя присущую математике красоту и увлекательность». Теперь рассмотрим химическую задачу. При сгорании 2,76 г ароматического углеводорода получили 9,24 г оксида углерода (IV) и 2,16 г воды. Относительная плотность этого вещества по водороду равна 39. Выведите молекулярную формулу этого вещества [4, c. 35, № 5.25*]. А на с. 62 к задаче 5.25 приводится ответ: C6H6. Проверим этот результат, для чего воспользуемся более надежными данными, определенными с точностью до трех значащих цифр: найдем, например, массу воды, образующуюся при сгорании 2,76 г или 2,76/78 = 0,0354 (моль) бензола по неполной схеме реакции 0,0354C6H6 → 0,106Н2О. Отсюда следует, что масса образовавшейся воды должна быть равна 0,106∙18= 1,91(г), что существенно отличается от массы воды 2,16 г в условии задачи. Значит, ответ C6H6 - неверный. Итак, как же найти правильный ответ к химической задаче? Поскольку более достоверными являются данные о массах, значения которых содержат по три значащие цифры, а плотность 39 – только две, то сначала лучше найти простейшую формулу, а затем используя Мr = 2∙39 = 78, – молекулярную. Запишем формулу углеводорода в общем виде CхHу, его ОММ Мr = 12х+у, неполную схему реакции 2 CхHу →уН2О и пропорцию: (2,76/(12х+у)):2= (2,16/18):у, х:у=7:8, т.е. C7H8 – простейшая формула углеводорода, для которого Мr = 92. Теперь, округлив 78/92 до натурального числа, т.е. до 1, придем к выводу, что простейшая формула C7H8 совпадает с молекулярной. Следовательно, относительная плотность углеводорода по водороду в условии задачи, записанная как 39,должна бытьзаменена на 92/2=46. Значит, ответ к задаче: C6H5 – CH3 (толуол) – правильный. Конечно, проверка в прикладных задачах – сложнее, чем в задачах математических. В последних числовые данные – точные, как, например, в рассмотренной выше. В химических задачах значения относительных атомных масс являются приближенными и такими же будут исходные данные, если они получаются экспериментально, на основе измерений. Итак, приближенные числа – это и сырье и продукция реальных вычислений. Именно поэтому при решении прикладных задач должны применяться правила приближенных вычислений. В этом контексте отметим, что в «Концепции развития математического образования в РФ», подчеркнуто: «Студенты, изучающие математику, включая информационные технологии,… должны уделять значительно больше времени, чем в настоящее время, решению творческих учебных и исследовательских задач». Как показали две последние задачи, посильную учебно-исследовательскую работу могут выполнять и учащиеся старших классов с углубленным изучением математики и химии. И подводя итог, подчеркнем, что рассмотренные в книге элементы научных исследований, связанные с построением и анализом математических моделей, будут полезны широкому кругу научных работников, инженеров, преподавателей, методистов, составителей задач, аспирантов, студентов, учащихся лицеев и классов с углубленным изучением математики и других предметов.
Литература 1. Арманд Д.Л. Как уточнялись знания о форме и величине Земли. Детская энциклопедия –Т.1. – М.: Просвещение, 1965.– 472 с. 2. Боднарский М.С. Представления древних народов о Земле. Детская энциклопедия Т.1. – М.: Просвещение, 1965. – 472 с. 3. Вентцель Е.С. Исследование операций: задачи, принципы, методология – М.: Наука,1988. – 208 с. 4. Гара Н. Н., Габрусева Н. И. . Химия. Задачник с «помощником». 10 —11 классы : пособие для учащихся общеобразовательных учреждений. Изд. 2 – е. — М.: Просвещение, 2013. — 79 с. 5. Гнеденко Б.В. Математика и математики в Великой Отечественной войне. – Квант. – 1985. – № 5. – С. 13. 6. Горстко А.Б. Познакомьтесь с математическим моделированием. – М.: Знание, 1991. – 160 с. 7. Гутер Р.С. . Янпольский А.Р. Дифференциальные уравнения.– М.: Физматгиз, 1962. – 248 с. 8. Демкович В.П., Прайсман Н.Я. Приближенные вычисления в школьном курсе физики.– М.: Просвещение, 1983. – 112 с. 9. Деркач М.И., Хрусталев А.Ф. М.В. Ломоносов и математическая химия. Химия в школе.–2011.– № 9. 10. Деркач М.И., Хрусталев А.Ф. Полезные «химические теоремы» Химия: Учебно-методический журнал для учителей химии и естествознания. «Первое сентября».– 2012. – № 3, с. 38-40. 11. Деркач М.И., Хрусталев А.Ф. Миленко Н.Н.. О метапредметном подходе к решению задач. Химия в школе.–2014.– № 3. 12. Детская энциклопедия. – М.:Просвещение,1965.– Т.2. – 521 с. 13. Дорофеев Г. В., Потапов М. К., Розов Н. Х. Математика: Для поступающих в вузы: Пособие. – М.: Изд-во «Дрофа», 1999. – 560 с. 14. Егоров А.С. Все типы расчётных задач по химии для подготовки к ЕГЭ. – Ростов н /Д: Изд-во «Феникс», 2004. – 320 с. 15. Ерыгин Д.П., Грабовый А.К. Задачи и примеры по химии с межпредметным содержанием. – М.: Высш. шк., 1989.– 176 с. 16. Задачи по географии: Пособие для учителей / Под ред. А.С. Наумова.– М.: Изд-во «Мирос», 1993. – 192 с. 17. Зак С.М., Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Все домашние работы к учебнику. Алгебра 9 класс. Учебник для общеобразовательных учреждений («Просвещение 2013 г. ФГОС). М.: «ЛадКом», 2014. – 288 с. 18. Ковалев Ф. В. Золотое сечение в живописи. Учеб. пособие. – К.:Выща школа,1989.– 143с. 19. Колмогоров А.Н., Ивашев-Мусатов О.С., Ивлев Б.М. Алгебра и начала анализа. Учеб. пособие для 10 класса средней школы. – М.: Просвещение, 1976. – 272 с. 20. Конфорович А. Г. Советские математики в годы Великой Отечест- венной войны// Математика в школе//Педагогика. 1975. – 1975.– №2.– С. 4–8. 21. Кремер Н.Ш., Путко Б.А., Тришин И.М. Высшая математика для экономистов. – М.: Изд-во «Юнити». 2006. – 440 с. 22. Любимова Н.Б. Вопросы и задачи по общей и неорганической химии. – М.: Высш. шк. 1990. – 351 с. 23. Макарычев Ю.Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Алгебра 8 класс: Учебник для общеобразовательных учреждений. Под. ред. С.А. Теляковского. – 15-изд., дораб. – М.: Просвещение, 2007. – 271 с. 24. Макарычев Ю.Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б: Алгебра. 9 класс: Учебник для общеобразовательных учреждений. Под. ред. С.А. Теляковского. – 17-изд. – М.: Просвещение, 2010. – 271 с. 25. Маршанова Г.Л. Сборник задач по органической химии. 10 – 11 классы. – М.: Изд-во «Школа». 2000. – 80 с. 26. Математика в современном мире. – М.: Мир, 1967. – 206 с. 27. Математика и научно-технический прогресс. – М.: Знание, 1972.– 64с. 28. Миленко Н.Н., Хрусталев А.Ф. Геометрия молекул: математические расчеты. Химия в школе.–2012.– № 7. 29. Мышкис А.Д. Элементы теории математических моделей. – М.: Изд-во «Едиториал УРСС», 2004. – 192 с. 30. Мышкис А.Д. Лекции по высшей математике. – М.: Наука, 1969. – 640 с. 31. Новиков Э.А. Планета загадок.–Л.: Недра, 1980. – 144 с. 32. Папкова А.С., Хрусталев А.Ф. Задача как аксиоматическая микросистема. Математические методы в механике, экономике, экологии: материалы ХI межд. студ. научн. конф. Севасто поль, 15 – 19 апреля 2013 г./ М-во образования и науки Украины; Севастоп. нац. техн. ун-т. – Севастополь: СевНТУ, 2013. – 104 с. 33. Папкова А.С., Хрусталев А.Ф. Теоремы об алканах и их приложения. Математические методы в механике, экономике, экологии: материалы ХII межд. студ. научн. конф. Севасто поль, 14 – 18 апреля 2014 г./ М-во образования и науки РФ; Севастоп. нац. техн. ун-т. – Севастополь: СевНТУ, 2014. – 100 с. 34. Романцева Л.М., Лещинская З.Л., Суханова В.А. Сборник задач и упражнений по общей химии. – М.: Высш. шк., 1991. – 288 с. 35. Рудзитис Г.Е., Фельдман Ф.Г. Химия: Органическая химия: Учебник для 10 кл. сред. шк. – М.: Просвещение, 1993.– 272с. 36. Самарский А.А. Что такое вычислительный эксперимент? Математическая модель //Что такое прикладная математика/А.А. Самарский. – М., 1980. – С.45. 37. Седов Л.И. Методы подобия и размерности в механике. – М.: Гостехиздат, 1954. – 228 с. 38. Скаткова Н.А., Хрусталев А.Ф. Применение ЭВМ к анализу устойчивости решений.// Вестник СевГТУ. – Севастополь, 1995. – №1 – С. 13-17. 39. Скаткова Н.А., Хрусталев А.Ф. ЭВМ совершенствует задачи. – Вестник СевГТУ. – Севастополь, 1998.– №12 – С. 40-43. 40. Тихонов А.Н., Костомаров Д.П. Рассказы о прикладной математике.–М.: Наука, 1979.– 207 с. 41. Хрусталев А.Ф. Молекулы и модели // Химия и жизнь.–1983. –№ 9. – С. 64. 42. Хрусталев А. Ф. И химику нужна математика //Химия и жизнь XXI век. – 1996. – № 1.– С. 78. 43. Хрусталев А.Ф. Теоремы гомологии // Химия и жизнь.– 1982. – № 5. – С. 72. 44. Хрусталев А.Ф. Теоремы математической химии //Вестник СевГТУ. Сер. Физика и математика. Вып. 43: Севастополь: Изд-во СевНТУ, 2003.– 176 с. 45. Хрусталев А.Ф. Наш поход к решению задач с избыточными даннями. Химия в школе.–2011.– № 4. 46. Хрусталев А. Ф. Основы математического моделирования : учеб. пособие для студентов вузов, обуч. по направлению подгот. «Физика»; М‑во образования и науки Украины, Севастоп. нац. техн. ун‑т ; [науч. ред. В. К. Маригодов]. — Севастополь : Изд-во СевНТУ, 2007. — 212 с. – Библиогр.: с. 204—207. — ISBN 978-966-2960-19-8. 47. Хрустальов О. Ф. Необхідно внести ясність // Вісн. СевНТУ : зб. наук. пр. / М‑во освіти і науки, молоді та спорту України, Севастоп. нац. техн. ун‑т. — Севастополь, 2011. — Вип. 119 : Механіка, енергетика, екологія. — С. 169—177. 48. Швец М.И. О приближенных числах. – К.: Радяньска шк., Энциклопедия элементарной математики. – М.;Л.: Гостехиздат; 1951. – Т.1. – 448 с.
СОДЕРЖАНИЕ Предисловие...................................................................................... 3 Введение............................................................................................. 5
§ 1. Математическое моделирование как метод познания.................... 7 1.1. Понятие математической модели.................................................... 7 1.2. О гуманитарной значимости математических моделей............... 10 1.3. О сущности аксиоматического метода.......................................... 12 1.4. Пример построения и исследования математической модели..... 13
§ 2. Общая схема применения математики. Множественность и единство моделей................................................................................................ 16 2.1. Общая схема применения математики............................ 16 2.2. Множественность и единство моделей............................ 17
§ 3. Требования, предъявляемые к математической модели.............. 21 3.1. Об адекватности математической модели....................... 21 3.2. О полноте математической модели................................. 23 3.3. О непротиворечивости модели........................................ 24 3.4. О других требованиях..................................................... 24
§ 4. Система линейных уравнений как математическая модель......................................................................................... 26 4.1. Химико-алгебраическое уравнение как модель реакции ………………………..…………………………26
§ 5. Приближенные числа и действия с ними........................... 30 5.1. Десятичная запись приближенных чисел.................................... 30 5.2. О приближенных числах и значащих цифрах............................ 30 5.3. О правилах действий с приближенными числами...................... 34 5.4. Об оценке точности решения....................................................... 34
§ 6. Устойчивость решений...................................................................... 36 ......
Поиск по сайту: |
 – количество машин, поставляемых с
– количество машин, поставляемых с  го завода
го завода  му автохозяйству, и из экономических соображений включим в план самую дешевую перевозку (8 ден. ед. за одну машину) в максимально возможном количестве со второго завода в первое автохозяйство,
му автохозяйству, и из экономических соображений включим в план самую дешевую перевозку (8 ден. ед. за одну машину) в максимально возможном количестве со второго завода в первое автохозяйство,  , тогда
, тогда  , т.е. самые дорогие перевозки не осуществляются, что естественно при минимизации их стоимости. Но тогда:
, т.е. самые дорогие перевозки не осуществляются, что естественно при минимизации их стоимости. Но тогда:  . Найденный план – оптимальный. Действительно, если уменьшим
. Найденный план – оптимальный. Действительно, если уменьшим  , то
, то  машин придётся перевозить по более высокой цене. А тогда стоимость перевозки возрастёт. Итак, экономический подход помог совсем просто найти решение рассматриваемой задачи.
машин придётся перевозить по более высокой цене. А тогда стоимость перевозки возрастёт. Итак, экономический подход помог совсем просто найти решение рассматриваемой задачи. , имеющего форму прямого кругового цилиндра, при изготовлении которого производится сварка швов по обоим основаниям и одной образующей, то здесь возникают две основные цели. Первая – минимизировать количество листового железа и вторая – минимизировать суммарную длину сварных швов. Нетрудно убедиться, что при заданном объёме
, имеющего форму прямого кругового цилиндра, при изготовлении которого производится сварка швов по обоим основаниям и одной образующей, то здесь возникают две основные цели. Первая – минимизировать количество листового железа и вторая – минимизировать суммарную длину сварных швов. Нетрудно убедиться, что при заданном объёме  ден. ед. Стоимость одного квадратного метра железа –
ден. ед. Стоимость одного квадратного метра железа – 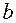 ден. ед.
ден. ед. м и высоту
м и высоту  м бака так, чтобы его стоимость была наименьшей.
м бака так, чтобы его стоимость была наименьшей. ,
, ,
, ,
, .
. при которых функция
при которых функция  принимает наименьшее значение. Подчеркнем, что в нашей модели все участвующие в ней величины безразмерные, так как они выражают только численные значения именованных величин (
принимает наименьшее значение. Подчеркнем, что в нашей модели все участвующие в ней величины безразмерные, так как они выражают только численные значения именованных величин (  >0, для построения вычислительного алгоритма можно воспользоваться таким методом. Возьмем начальную точку
>0, для построения вычислительного алгоритма можно воспользоваться таким методом. Возьмем начальную точку  вблизи начала координат и некоторый шаг
вблизи начала координат и некоторый шаг  и будем последовательно вычислять значение
и будем последовательно вычислять значение 
 , сравнивая получaемые числа
, сравнивая получaемые числа  ,
, 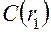 ,
,  , … , которые сначала будут убывать, а затем возрастать.
, … , которые сначала будут убывать, а затем возрастать. ], на котором достигается наименьшее значение функции
], на котором достигается наименьшее значение функции  , причём значение
, причём значение  будет вычислено с точностью
будет вычислено с точностью  . Если требуемая точность решения задачи еще не обеспечена, то следует уменьшить шаг
. Если требуемая точность решения задачи еще не обеспечена, то следует уменьшить шаг 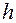 в несколько раз и повторить описанную процедуру, начиная с
в несколько раз и повторить описанную процедуру, начиная с  .
. с шагом вычислений 0,05.
с шагом вычислений 0,05.
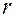
 .
.
 .
. и убедимся в том, что
и убедимся в том, что  и
и  , что также подтверждает наличие минимума
, что также подтверждает наличие минимума  .
. по возможности меньшее значение, то не требуется слишком точно находить точку минимума, так как это практически не повлияет на значение функции» [24, с. 67], что наглядно представлено на рисунке 23.1.
по возможности меньшее значение, то не требуется слишком точно находить точку минимума, так как это практически не повлияет на значение функции» [24, с. 67], что наглядно представлено на рисунке 23.1.

 .
. и
и  с точностью до одной сотой и в этих случаях
с точностью до одной сотой и в этих случаях  и нижний
и нижний 
 позволяет сформулировать результат в терминах исходной задачи и дать практическую рекомендацию. При изготовлении бака следует учитывать его оптимальные размеры: радиус основания бака должен быть примерно равен 0,28 м, высота 1,0 м. В этом случае стоимость бака составит около 136 ден. ед.
позволяет сформулировать результат в терминах исходной задачи и дать практическую рекомендацию. При изготовлении бака следует учитывать его оптимальные размеры: радиус основания бака должен быть примерно равен 0,28 м, высота 1,0 м. В этом случае стоимость бака составит около 136 ден. ед. при
при  . Расчет показывает, что при этом условии
. Расчет показывает, что при этом условии  ,
,  . Если по этим формулам при
. Если по этим формулам при  , что совпадает с результатами, полученными при анализе функции стоимости
, что совпадает с результатами, полученными при анализе функции стоимости  при
при  .
.
 . Расчет показывает, что при этом условии
. Расчет показывает, что при этом условии  ,
,  .
. .
. принимает наименьшее значение.
принимает наименьшее значение. , то, решая уравнение
, то, решая уравнение  , находим
, находим  ,
,  .
. , функция
, функция  будет большой. Так как
будет большой. Так как  только при одном значении
только при одном значении  , то ему и соответствует наименьшая длина сварных швов.
, то ему и соответствует наименьшая длина сварных швов. при
при 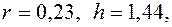 что совпадает с результатами, полученными при анализе функции стоимости
что совпадает с результатами, полученными при анализе функции стоимости  при
при  .
.
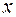 и
и 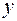 соответственно число десятков и единиц двузначного числа, для нахождения неизвестных получим уравнение
соответственно число десятков и единиц двузначного числа, для нахождения неизвестных получим уравнение – натуральные числа, причем у – четное, у ≠ 0 и значит,
– натуральные числа, причем у – четное, у ≠ 0 и значит,
 , так как
, так как 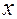 – натуральное число. Следовательно, из (3) имеем:
– натуральное число. Следовательно, из (3) имеем:  ,
,  , но это число не является натуральным. Снова приходим к выводу, что двузначного числа, о котором идет речь, не существует. Просто и красиво!
, но это число не является натуральным. Снова приходим к выводу, что двузначного числа, о котором идет речь, не существует. Просто и красиво!