 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Докажите теорему о разрешимости задачи линейного программирования на минимум. ⇐ ПредыдущаяСтр 6 из 6
Теорема. (о разрешимости задачи линейного программирования на минимум) Если каноническая задача линейного программирования на минимум имеет допустимое решение, а целевая функция на множестве допустимых решений ограничена снизу, то эта задача имеет оптимальное решение. ▲ В теореме о существовании опорного решения было доказано, что если каноническая задача линейного программирования имеет допустимое решение, то эта задача имеет и опорное решение. Принимаем это опорное решение за начальное опорное решение и решаем задачу симплекс методом. Так как целевая функция ограничена снизу на множестве допустимых решений, то через конечное число шагов симплекс метода будет найдено оптимальное решение данной задачи. ■ Теорема(о существовании опорного решения). Если каноническая задача линейного программирования имеет хотя бы одно допустимое решение, то эта задача имеет и опорное решение. ▲ Рассмотрим КЗЛП (6) f(X) = (7) (8) xj ≥ 0, j = 1,2,…,n, которая имеет хотя бы одно допустимое решение. Из всех допустимых решений данной задачи выберем допустимое решение с наименьшим числом ненулевых координат. Пусть таким решением будет вектор α = ( α1, …, α Предположим противное, а именно, что вектор α не является опорным решением. Тогда по определению опорного решения, векторы A1, A2, … A (9) A1 k1 + A2 k2 + … + A Так как вектор α является допустимым решением рассматриваемой задачи, то по определению, этот вектор является решением системы линейных уравнений (2). Тогда по определению решения системы уравнений должно выполняться соотношение (10) A1 α 1 + A2 α 2 + … + A Прибавив к соотношению (5) соотношение (4), умноженное на А1( α1 Из последнего соотношения по определению решения системы уравнений следует, что векторы α’ = ( α1 + δ k1, α2 + δ k2, … α 39.Теорема (об оптимальном решении). Если каноническая задача линейного программирования (1) – (3) имеет оптимальные решения, то одно из них является опорным решением этой задачи. ▲ Рассмотрим оптимальное решение задачи (1) – (3) с наименьшим числом ненулевых координат. Пусть таким решением будет вектор α0 = ( α1, …, α Предположим противное, а именно, что вектор α0 не является опорным решением. Тогда по определению опорного решения, векторы A1, A2, … A A1 k1 + A2 k2 + … + A Так как вектор α0 является оптимальным решением, то он является и допустимым решением рассматриваемой задачи, то есть, этот вектор является решением системы линейных уравнений (2). Тогда по определению решения системы уравнений должно выполняться соотношение A1 α 1 + A2 α 2 + … + A Прибавив к соотношению (5) соотношение (4), умноженное на А1( α1 Из последнего соотношения по определению решения системы уравнений следует, что векторы α’ =( α1 + δ k1, α2 + δ k2 , … α
f(α0) ≤ f(α’’), которая равносильна системе:
Откуда получаем противоречивую систему:
0 ≤ – δ Таким образом, предположение о том, что вектор α0 не является опорным решением не верно. Следовательно, вектор α0 является опорным решением задачи (1) – (3). ■
Поиск по сайту: |
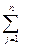 γj xj + γ0,
γj xj + γ0,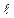 , 0, …, 0), где координаты α1> 0, …, α
, 0, …, 0), где координаты α1> 0, …, α  δ, получим
δ, получим f(α0) < f(α’),
f(α0) < f(α’),
 0 < δ
0 < δ