 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Пример Метод собственных значений
Частные решения неоднородной системы Найти частное решение неоднородного уравнения, соответствующее заданным начальным условиям.
1)Найдем общее решение соответствующего однородного уравнения: 2) Частное решение неоднородного уравнения ищем в виде:
Подставим Таким образом: 3) Общее решение неоднородного уравнения: 4) Найдем частное решение, соответствующее заданным начальным условиям: Ответ: частное решение: Способы построения частного решения неоднородной системы Найти частное решение неоднородного уравнения, соответствующее заданным начальным условиям.
1)Найдем общее решение соответствующего однородного уравнения: 2) Частное решение неоднородного уравнения ищем в виде: Подставим Таким образом: 3) Общее решение неоднородного уравнения: 4) Найдем частное решение, соответствующее заданным начальным условиям: Ответ: частное решение:
Фазовое пространство и фазовые траектории автономной системы. Свойства решений и фазовых траекторий. Автономные системы дифференциальных уравнений x˙=f(x,y) { (1) y˙=g(x,y) Траекторией (или фазовой кривой) системы (1) называется кривая, параметрически задающаяся как (x,y)=(x(t),y(t)), где (x(t),y(t)) — некоторое решение системы (1). Пространство R^2 называется фазовым пространством системы (1). Его точки – состояние системы. Фазовые траектории являются проекциями интегральных кривых на плоскость R^2. Свойства решений и фазовых траекторий: 1) фазовые траектории либо не пересекаются, либо совпадают 2) точка х=а (принадлежит R^2) такая, что f(a)=0 называется положением равновесия системы (1) 3) система (1)может иметь фазовые траектории только следующих типов: гладкие кривые без самопересечений замкнутые гладкие кривые(циклы) точки (положения равновесия) Циклы соответствуют периодическим решениям, а точки – положениям равновесия.
Поиск по сайту: |

 ,
,  ,
, 
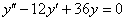

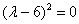
 – кратные действительные корни
– кратные действительные корни
 (предварительно смотрим Раздел III справочной таблицы).
(предварительно смотрим Раздел III справочной таблицы).

 и
и  в левую часть неоднородного уравнения:
в левую часть неоднородного уравнения:

 .
.


