 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предел и непрерывность отображений метрических пространств
Под отображением метрических пространств будем понимать отображение множества элементов некоторого метрического пространства в множество элементов другого (или того же) метрического пространства. Далее метрическое пространство и его множества будем обозначать одной буквой X или Y, а метрику соответственно rX и rY. Пусть f – отображение из метрического пространства X в метрическое пространство Y, т.е. f: Х Определение 1. (на языке последовательностей). Точка а называется пределом отображения f в точке х0, если для любой последовательности (xn), сходящейся к хo по метрике rх, с членами из D( f ) неравными хо, соответствующая последовательность (f(xn))сходится к а по метрике ry. Определение 2.(на языке “e-d”). Точка а называется пределом отображения f в точке хо, если для любого положительного числа e существует положительное число d(e) такое, что для всех точек х, принадлежащих D( f ) и удовлетворяющих условию 0<rx(x,xo)< d, выполняется неравенство rY(f(x),а)<e. Если точка а является пределом отображения f в точке хо, то пишут Сформулированные выше определения символично можно записать так: Опр.1: Опр.2: Сформулируем определение 2 в разных метрических пространствах. Пример 1. Пространство R1: X = R, Y = R; f: R
Пример 2. Пространство R2: X = R2, Y = R, f: R2 Теорема 1.Определении 1 и 2 равносильные. Доказатьельство самостоятельно(см. 1 курс). Определение 3. Пусть f – отображение из метрического пространства X в метрическое пространство Y (f: Х Замечание 1.В этом определении не требуется, чтобы точка хо была предельной точкой D( f ). Она может быть и изолиированной точкой D( f ). Геометрический смысл Определения 3: отображение f: Х Определение 3'. Если точка хо – предельная точка D( f ), то отображение f непрерывнае в точке хо тогда и только тогда, когда Если точка хо – изолированная точка D( f ), то отображение f считаем непрерывным в точке хо. Определение 4. Отображение f: Х ® Y называется непрерывным на множестве МÌХ, если яно непрерывное каждой точке множества М. Если М =Х, то отображение f: Х ® Y называется непрерывным. Теорема 2. (Критерий непрерывности отображения) Отображение f: Х®Y является непрерывным тогда и только тогда, когда при этом отображении прообраз любого открытого (замкнутого) в Y множества есть множество открытое (замкнутое) в Х. Т.е., если множества GÌY – открытое (замкнутое) множество, то множество f -1(G) – открытое (замкнутое) в Х. Докажем для случая открытого множества. Дано
Доказать: f — непрерывное отображение. ◄
► Дано непрерывное отображение f: Х Доказать: ◄
► Для случая замкнутого множества Е нужно рассмотреть его дополнение СЕ – открытое множество и воспользоваться уже доказанной частью. Определение 5. Отображение f: Х Замечание 2.Если отображение f: Х Определение 6. Метрическое пространство Х называется связанным, если его нельзя представить в виде двух непустых непересекающихся между собой открытых (в виде двух непустых непересекающихся между собой замкнутых) множеств. Определение 7. Множество ЕÌХ называется связаннымв м.пр. Х, если связанным является подпространство Е метрического пространства Х. Пример 3. В пространстве R связанными являются интервал, отрезок, луч, множество {3}; Пример 4. В пространстве R2связанным является любое множествоЕÌ R2 , удовлетворяющее условию: любые две точки из Е можно соединить ломанной, которая полностью лежит в Е. Например, кальцо; Пример 5. Множество Е = (0,1)È[3,4]Ì Rне является связанным множеством. Теорема 3.Если отображение f связанного метрического пространства Х в метрическое пространство Y – непрерывное, то множество f(X)связанное в Y. 3Методом от противного. Пусть множества f(X) не является связанным в м.пр. Y. Это означает, что существуют два непустых, непересекающихся между собой открытых множества М и N таких, что f(X) = MÈN. Па теореме 2 в силу непрерывности отображения f прообразы множеств М и N будут открытыми (f –1(M) , f –1(N)). Очевидно, что они будут также непустыми, непересекающихся между собой множествами, а их объединение есть Х. Но это значит, что пространство Х не является связанным, что противоречит условию теоремы о связанности метрического пространства Х.►
Поиск по сайту: |
 Y, точка аÎY, x0 – предельная точка D( f ) (D( f ) – область определения отображения f из пространства X в пространство Y).
Y, точка аÎY, x0 – предельная точка D( f ) (D( f ) – область определения отображения f из пространства X в пространство Y).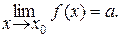

 R.
R. —открытое множество.
—открытое множество.