 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства сходящихся последовательностей в некоторых
метрических пространствах Теорема 1(о покоординатной сходимости последовательности в м. пр. Rm). Для того, чтобы последовательность точек метрического пространства Rm (хn =(х1(n),х2(n),…, хm(n)) сходилась к точке а =(а1,а2,…, аm) этого пространства необходимо и достаточно чтобы числовые последовательности (х1(n)), (х2(n)),…,(хm(n)) (соответствующих координат) стремились соответственно к числам а1,а2,…, аm , т.е.
Если выполняются равенства (1), то говорят, что последовательность (хn)сходится к точке а покоординатно. 31. Пусть Докажем, что выполняются равенства (1). В силу равенства (2) (по определению предела последовательности) в м.пр. Rm будем иметь: "e>0 $N(e)½"n>N Þ r( xn,а)<e, где r - метрика метрического пространства Rm :
4 32. Пусть выполняются равенства (1). Докажем, что Пусть e - любое положительное число рассмотрим число
Пример 1.Найти предел a = (a1,a2) последовательности в пространстве R2.
Таким образом, Теорема 2(Больцана-Вейерштрасса в м.пр. Rm). Из всякой ограниченной последовательности пространства Rmможно выделить сходящуюся подпоследовательность. Частный случай этой теоремы для пространства R1был доказан на первом курсе. Теорема 3.Для того, чтобы последовательность (xn) точек м.пр. С[a,b] с чебышёвской метрикой сходилась к элементу х этого м.пр., необходимо и достаточно, чтобы функциональная последовательность (xn)равномерно сходилась к х на [a,b]. Докажем с помощью критерия равномерной сходимости. 3Известно, что фукциональная последовательность (xn) равномерно сходится к предельной фукции х тогда и только тогда, когда
С учётом определения метрики в м.пр. С[a,b]получаем равенство
Пример 2.xn(t) = tn "tÎ[0;1/2]Ù"nÎN. известно, что на [0;1/2] фукциональная последовательность xn(t) = tn равномерно сходится к предельной фукции x (t) = 0. Таким образом "tÎ[0;1/2] последовательность (xn) сходится к функции х = 0 в м.пр. С[0;1/2]. Теорема 4. Если а – предельная точка множества Е метрического пространства (X, r), то существует последовательность (xn), члены которой принадлежат Е и не равны а, причём (xn), сходится к а в этом метрическом пространстве. Доказатьельство аналагично доказатьельству в пространстве R. Замечание 1. Поскольку любая норма задает метрику, rо(x,y) = то в нормированном пространстве А также можно определить предел последовательности элементов нормированного пространства. Замечание 2. Поскольку предгильбертовое пространство является нормированным пространством с нормой §9. Полные метрические пространства Определение 1. Последовательность (xn) метрического пространства (Х, r)называется фундаментальной, если
Примером фундаментальной последовательности является любая сходящаяся последовательность точек метрического пространства. В пространствеRлюбая фундаментальная последовательность – сходящаяся. Но для любого м.пр. не всякая фундаментальная последовательность метрического пространства (Х, r)сходится в этом пространстве. Пример 1. В м.пр. Х = (Q; r =½х- у½) последовательность – фундаментальная, но с 1 курса известно, что но е Ï X (е ÎI). Определение 2. Метрическое пространство называется полным метрическим пространством, если любая фундаментальная последовательность точек этого пространства сходится в нем. Пример 2. Метрическое пространство R – полное метрическое пространство, т.к. любая фундаментальная последовательность сходится к числу, из пространства R. Это следует из критерия Коши (см. 1 курс). Пример 3. Докажем, что пространство Rm- полное метрическое пространство. 3Пусть последовательность(xn= x1(n), x2(n),…, xm(n)) (1) любая фундаментальная последовательность пространстваRm. Покажем, что эта последовательность сходящаяся и её предел принадлежит пространству Rm. Па определению фундаментальной последовательности и определению метрики в пространствеRm "e>0$ N(e)ÎN½" p,n >N Þ r(xp,xn)<e Þ Согласно доказатьельству теоремы 1 §8 Таким образом, была доказана фундаментальност числовых последовательностей (x1(n)), (x2(n)),…, (xm(n)), а значит и их сходимость (по критерию Коши). Пусть Рассмотрим точку а = (а1, а2, …, аm). Т.к. а1, а2, …, аmÎR, то аÎRm. По теореме 1 §8 получаем, что в м.пр. Rm последовательность (xn) сходится к аÎRm . Это означает, что пространствоRm полное метрическое пространство. 4 Пример 4.Докажем, что метрическое пространство С[a,b] является полным. 3Пусть (xn) – любая фундаментальная последовательность в м.пр. С[a,b] , её члены – непрерывные на [a,b] фукции. Докажем, что последовательность (xn) сходится в метрическом пространстве С[a,b]. Сначала покажем, что она сходится к предельной фукции х на отрезке [a,b]. По определению фундаментальной последовательности (2) Это означает, что "tÎ[a,b] (фиксируем t) фундаментальной является числовая последовательность (xn (t)). Значит она имеет предел, который обозначим через Покажем, что предельная фукция x(t) непрерывная на [a,b]. Для этого в неравенстве (2) §прейдём к пределу при m®¥. Получим ½ x (t)- xn(t)½ £ e "n>N Ù "tÎ[a,b]. Таким образом, мы доказали, что "e>0$NÎN½"m,n > N Þ½ x (t)- xn(t)½ £ e "tÎ[a,b]. А это значит, что последовательность (xn) равномерно сходится к фукции х на [a,b]. Т.к. все члены последовательности (xn) непрерывные на [a,b]фукции, то предельная фукция также непрерывная на этом отрезке, т.е является элементом метрического пространства С[a,b]. По теореме 2 §8 в этом пространстве последовательность (xn) сходится к х. Значит пространствоС[a,b] – полное метрическое пространство. 4 Определение 3. Полное нормированное пространство называется Банохавым пространством. Банохавыми пространствоми, являются пространства: Rп с нормами l2 с нормой векторов x = (xn) = (x1, x2, …) ; C [a,b] с нормой функций x(t) А пространство C1 [a,b] с нормой не является баноховым. Определение 2.Полное предгильбертовое пространство относительно нормы (2) §3 называется гильбертовым пространством. Примерами гильбертовых пространств являются перечисленные пространства из примеров §4. Предгильбертовое пространство из примера 3 §4 не является полным относительно нормы (2) и поэтому не является гильбертовым.
Поиск по сайту: |
 ,
,  ,...,
,..., 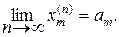 (1)
(1) в м.пр. Rm. (2)
в м.пр. Rm. (2) "x,yÎRm.
"x,yÎRm. . Тогда
. Тогда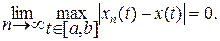
 (см. опр. 4 §7)
(см. опр. 4 §7)  по метрике r в м.пр. С[a,b]. 4
по метрике r в м.пр. С[a,b]. 4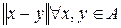
 , то в предгильбертовом пространстве также можно определить предел последовательности элементов предгильбертового пространства.
, то в предгильбертовом пространстве также можно определить предел последовательности элементов предгильбертового пространства.



 для каждого фиксированного tÎ[a,b].
для каждого фиксированного tÎ[a,b]. ,
,  ;
; .
.