 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Классификация точек и множеств в метрических пространствах
Пусть (Х, r) – метрыческое пространство. Определение 1. с центром в точке хо и радиусом e называется множество всех точек хÎХ, удовлетворяющих условию r(x,хо)< e. Это множество называется также e-окрестностью точки хо и обозначается U(xo, e) или Ue(xo). Пример 1.Открытый шар в разных пространствах: в пространстве R1:(xo- e; xo+ e) – интэрвал; в пространстве R2: открытый круг; в пространстве R3:открытый шар. Определение 2 с центром в точке хо и радиусом e называется множество всех точек хÎХ, удовлетворяющих условию r(x,хо)£ e. Будем говорить шар,подразумевая определение 2. Под сферой будем понимать множества точек хÎХ, удовлетворяющих условию r(x,хо) = e. Пример 2. Шар в разных пространствах: в пространстве R1:[xo- e; xo+ e] – отрезок; в пространстве R2: замкнутый круг или просто круг; в пространстве R3:замкнутый шар или просто шар. Определение 3. Множества ЕÌХ называется ограниченным в метрическом пространстве(Х, r), если существует шар канечного радиуса, включающий это множество. Замечание 1.Одно и тоже множество может быть ограниченным в одном метрическом пространстве и неограниченным в другом. Пример 3.Интервал (3;5) Ì R – множество ограниченное в пространстве R; интервал (3;5) – неограниченное множество в пространстве Х =(3;5), r(x,y) = ½х-у½, которое является подпространством R. Определение 4. Пусть ЕÌХ. Точка х0 называется множества Е, если в любой окрестности этой точки находятся точки, как принадлежащие множеству Е так и не принадлежащие ему. Множество граеичных точек называется границей множества Е и обозначается ¶Е. Пример 4.Множество Е1 = ( 0;1] Ì R Þ ¶Е1 = { 0;1}; множество Е2 = ( 0;1] Ì Х (Х= ( 0;1], r(x,y) = ½х- у½) не имеет границы. Замечание 2. Граничные точки множества могут как принадлежать множеству, так и не принадлежать ему. Определение 5. Точка х0 называется множества Е, если существуетокрестность точки х0, которая полностью лежит в множестве Е. Множество всех внутренних точек называется внутренностью множества Е и обозначается Пример 5.В метрическом пространстве R рассмотрим множества Е1 = (2;3), Е2 = (2;3], Е3 = [2;3]. Для них Пример 6. В метрическом пространстве Х (Х= ( 2,3]È {4,5}, r(x,y)=½х-у½) – подпространстве м.пр. R, Определение 6. Если каждая точка множества Е – внутренняя, то Е называется , т.е. для открытого множества: В примере 5 множество Е1 является открытым, а множества Е2 и Е3 не является открытыми. В примере 6 множество Е2 является открытым, а Е3 не является открытыми. Пример 7.Любой интервал (a,b)является открытым множеством в метрическом пространстве R. Определение 7. Точка хо называется множества Е, если в любой её окрестности находится бесконечно много точек из множества Е. Другими словами точка хо называется предельной точкой множества Е, если в любой её окрестности находится хотя бы однаточка множества Е, отличная от хо. Множество всех предельных точек множества Е называется производныммножеством множества Е и обозначается Е¢. Замечание 3. Предельные точки могут как принадлежать множеству Е, так и не принадлежать ему. Определение 8. Если множество ЕÌХ содержит все свои предельные точки, то оно называется замкнутым. Пример 8.В пространстве R :Е1 = (a,b), Е1¢ = [a,b]; E2 = [a,b], Е2¢ = Е2; Е3 = ( 2,4)È{6}; Е3¢ = [2,4]. Пример 9. Пустое множества – замкнутое множество. Определение 9. Точка хо Î Е называется точкой множества ЕÌХ, если существует e - окрестность этой точки, в которой нет других точек из множества Е, кроме точки хо . Замечание 4. Каждая точка множества Е является предельной или изолированной. Пример 10.В метрическом пространстве R каждая точка множества Е={0,1,1/2, 1/3, …}, кроме точки 0, является изолированной; точка 0 – предельная точка множества Е. Определение 10.Точка хо называется множества ЕÌХ, если любая её e - окрестность содержит хотя бы одну точку множества Е. Из определений 7, 9 и 10 вытекает, что любая точка преткновения множества Е может быть либо предельной точкой множества Е, принадлежащей множеству Е; либо предельной точкой множества Е, не принадлежащей множеству Е; либо изолированной точкой множества Е. Определение 11.Множество всех точек преткновения множества Е называется множества Е и обозначается Замечание 5. Замечание 6. Множество замкнутое, если оно совпадает со своим замыканием. Определение 12. Дополнениеммножества ЕÌХ до множества Х называется множество всех точек из множества Х, которые не принадлежат множеству Е. Обозначают это множество СхЕ или СЕ. §6. Теоремы об открытых и замкнутых множествах Теорема 1.Объединение любого числа открытых множеств – множество открытое. Пусть Gk – открытые множества. Докажем, что 3Возьмем любую точку хо ÎG. По определению объединения множеств точка хо будет принадлежать хотя бы одному из множеств Gk . Т.к. Gk – открытые множества, то существует e - окрестность точки хо, которая полностью принадлежит множеству Gk : Получили, что любая точка хо ÎG – внутренняя, а это означает, что G – открытое множество. 4 Теорема 2.Пересечение конечного числа открытых непустых множеств – множество открытое. Пусть Gk ( k = 1,2, …,n) – открытые множества. Докажем, что 3Возьмем любую точку хо ÎG. По определению пересечения множеств хо принадлежать каждому из множеств Gk. Т.к. множества Gk открытые, то в любом множестве Gk существует ek- окрестность точки хо: U( xo, e k) Ì Gk. Множество чисел{e1, e2,…, en } конечное, поэтому $ e = min {e1,e2,…,en}. Тогда e - окрестность точки хо принадлежит каждой ek- окрестности точки хо: Получили, что хо – внутренняя точка множества G, а это значит, что G – открытое множество. 4 Замечание 1.Пересечение бесконечного числа открытых множеств может и не быть аоткрытым множеством. Пример 1. Пусть в пространстве R где k=1,2,…,n,….
Теорема 3. Пересечение бесконечного числа замкнутных непустых множеств– замкнутое множество. Пусть Fk – замкнутые множества. Докажем, что множества
Теорема 4. Объединение конечного числа замкнутных непустых множеств– замкнутое множество. Пусть множества Fk – замкнутые. Докажем, что множество
Замечание 2. Объединение бесконечного числа замкнутых множеств может быть множеством открытым. Пример 2. В пространстве R: Fk =[2+1/k;5–1/k] Теоремы 5 и 6, связанны с дополнением множества Е до множества Х: СхЕ=СЕ. Теорема 5. Если множество Е замкнутое, то его дополнение до множества Х: СхЕ=СЕ – открытое множество. ►
◄ Пример .3. Е= [2,5], CR E = Теорема 6.Если множество Е открытое, то его дополнение до множества Х: СхЕ=СЕ – замкнутое множества. ►
◄ Пример 4. Е= (2,5), CR E = §7. Последовательности точек метрического пространства Определение 1.Последовательностью точек метрического пространства (Х, r)называется отображение f множества натуральных чисел N в множество Х: f: N Значение этого отображения в точке n Î N называется n-м членом последовательности точек метрического пространства и обозначается xn = f(n). Последовательность будем обозначать(xn)или (х1,х2,…, хn…). Пример 1. В пространстве R2 : хn = (1¤n, n+1/n)); Пример 2. В пространстве С[a,b]: (хn = (1/nx + n2x )) где [a,b] не содержит 0. Определение 2.Пусть (xn) – последовательность точек метрического пространства (Х, r), (k1,k2,…, kn,…) – возрастающая последовательность натуральных чисел. Тогда последовательность(xkn) называется подпоследовательностю последовательности (xn). Пример 3.Последовательность (1/n2) – подпоследовательность последовательности (1/n). Определение 3.Пусть (xn)– последовательность точек метрического пространства (Х, r), Последовательность(xn) называется ограниченной, если существует замкнутый шар с центром а и конечным радиусом R, который содержит все члены последовательности, т.е. Замечание 1. Панятие монотонной последовательности можно ввести не во всех метрических пространствах. Определение 4. Пусть (xn)– последовательность точек метрического пространства (Х, r). Точка а Î Х называетсяпределом последовательности (xn) если: "e >0$N(e) Î N ½"n > N(e), n Î N Þ r(xn,a) < e; или, что тоже самое, числовая последовательность (r(xn,a)) — бесконечно малая (стремится к 0), при n®¥ ,т.е. и абазначаецца
Если последовательность (xn) имеет конечный предел, то она называется сходящейся, в противном случае – расходящейся. Если (xn) – последовательность точек метрического пространства (Х, r) сходится к точке аÎХ, то а – предельная точка последовательности (xn). Обратное не всегда имеет место. Замечание 2. Одна и та же последовательность в разных метрических пространствах может как сходиться, так и расходиться Пример 4.Последовательность (1/n) сходится в пространстве R, но расходится в пространстве (Х,r), где Для сходящихся последовательностей справедливы теоремы. Теорема 1. Если (xn) – сходящаяся последовательность метрического пространства (Х, r), то её предел единственный. 3Пусть
По аксиомам метрики 0 £ r(a,b) £ r( xn,a) + r(xn,b). Переходим к пределу, при n®¥, Получим r(a,b) = 0 Û a=b. 4 Теорема 2. Если (xn) – последовательность точек метрического пространства (Х, r) – сходящаяся, то она ограниченная. 3Пусть
Теорема 3.Если (xn) – последовательность точек метрического пространства (Х, r)сходится к точке а Î Х, то любая её подпоследовательность сходится к а. 3Пусть Т.к. kn ³ n, то для всех n>N верно kn >N и поэтому r Таким образом мы доказали, что "e>0 $N(e)½"n>N Þ r
Поиск по сайту: |
 .
. =
= 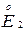 =
=  = (2;3).
= (2;3). .
. – открытое множество.
– открытое множество. – открытое множество.
– открытое множество.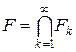 замкнутое, т.е. оно содержит все свои предельные точки.
замкнутое, т.е. оно содержит все свои предельные точки. замкнутое, т.е., если хо – предельная точка множества F, то хоÎ F.
замкнутое, т.е., если хо – предельная точка множества F, то хоÎ F.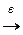 X.
X.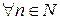
 .
.

 по метрике r или
по метрике r или  , при n®¥.
, при n®¥. r(x,y)=½х-у½, т.к. 0
r(x,y)=½х-у½, т.к. 0  .
.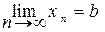 Û r(xn,b)® 0.
Û r(xn,b)® 0.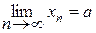 .
. – любая подпоследовательность последовательности(xn). По условию
– любая подпоследовательность последовательности(xn). По условию 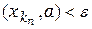 .
. .4
.4