|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Геометрическая интерпретация задач линейного программирования. Графический метод.
Для решения задач ЛП с двумя переменными, а также некоторых задач с тремя переменными используется графический метод. Рассмотрим его на конкретных примерах. Пример 1. Для производства двух видов изделий А и В предприятие использует три вида сырья. Другие условия задачи приведены в таблице.
Составить план выпуска продукции, при котором прибыль предприятия от реализации продукции будет максимальной. Обозначим количество единиц k-го вида изделий, выпускаемых предприятием, через xk, к=1,2.Экономико-математическая модель этой задачи имеет такой вид:
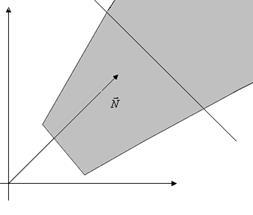
Каждое из неравенств системы ограничений определяет полуплоскости, пересечение которых дает многоугольник допустимых планов. Построить его можно так. Сначала строим граничные прямые Теперь рассмотрим целевую функцию
Линии уровня этой функции, например, На практике строят вектор градиент целевой функции, координаты которого -коэффициенты целевой функции В нашем случае – это вершина В. Чтобы найти её координаты необходимо решить систему уравнений
Решение системы
Пример 2. Найти максимум функции Z=4x1+3x2 при условиях
Каждое из этих неравенств определяет полуплоскости, пересечение которых дает многоугольник, заштрихованный на рисунке. Этот многоугольник (выпуклый многогранник) и представляет собой допустимое множество решений задачи ЛП
Теперь рассмотрим целевую функцию Z=4x1+3x2,пусть ее значение Z=12000=Z1.График уравнения 4х1+3х2=12000 - прямая с отрезками на осях x1=3000; x2=4000. При Z=24000 получим прямую z2. Прямая z2 параллельная прямой z1, но расположена выше от нее. Передвигая прямую z вверх параллельно самой себе, приходим к такому ее положению, когда прямая и многоугольник решений будут иметь только одну общую точку –вершину многоугольника решений. Очевидно, что точка А (x1=2000; x2=6000) - оптимальное решение, так как она лежит на прямой с максимально возможным значением целевой функции Алгоритм графического метода решения задач линейного программирования состоит из следующих шагов: ü Строим прямые уравнения которых получаем заменой в ограничениях (2') задачи линейного программирования знаков неравенства на знаки равенства.
ü Определяем полуплоскости которые отвечают каждому ограничению задачи.
ü Определяем многогранник решений задачи линейного программирования.
ü Строим вектор
ü Строим прямую
ü Двигая прямую
ü Определяем координаты точки в которой целевая функция принимает максимальное (минимальное) значение и находим экстремальное значение целевой функции в этой точке. Если задача линейного программирования имеет оптимальный план, то экстремальное значение целевая функция принимает в одной из вершин многогранника решений. Если целевая функция достигает экстремальное значение больше чем в одной из вершин многогранника то она достигает его и в любой точке которая есть линейной комбинацией этих вершин. В случае применения графического метода к решению задач линейного программирования возможны такие случаи: I. Целевая функция принимает максимальное значение в единственной вершине А многогранника решений ( см. рис.1 )) Рис.1 II. Максимальное значение целевая функция принимает в любой точке отрезка – стороны многоугольника решений (рис.2 ). В этом случае задача линейного программирования имеет альтернативные оптимальные планы.
Рис.2 III. Задача линейного программирования не имеет оптимальных планов: если целевая функция неограниченна сверху (рис. 3) либо система ограничений задачи является несовместной (рис.4 ).
Рис.3
Рис.4 IV. Задача линейного программирования может иметь оптимальный план при условии неограниченной области допустимых решений . На рис. 5 целевая функция имеет максимум, на рис.6 - минимум в случае неограниченной области допустимых планов, целевая функция может также принимать максимальное или минимальное значение в произвольной точке луча.
Рис.5
Рис.6
Поиск по сайту: |



 ,
, 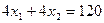 , и
, и  . Потом выбирая удобные точки, например,
. Потом выбирая удобные точки, например,  , проверяем удовлетворяют ли их координаты соответствующие неравенства. Если да, то выбираем полуплоскость которой принадлежит точка. Если нет, то соответственно- другую полуплоскость. Пересечение выбраных плоскостей – это многоугольник, состоящий из точек, координаты которых удовлетворяют всем ограничениям, то есть – это область допустимых планов задачи. Итак, пятиугольник ОАВСД - многоугольник решений данной задачи
, проверяем удовлетворяют ли их координаты соответствующие неравенства. Если да, то выбираем полуплоскость которой принадлежит точка. Если нет, то соответственно- другую полуплоскость. Пересечение выбраных плоскостей – это многоугольник, состоящий из точек, координаты которых удовлетворяют всем ограничениям, то есть – это область допустимых планов задачи. Итак, пятиугольник ОАВСД - многоугольник решений данной задачи 
 .
.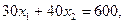
 и так далее, -это параллельные прямые. Двигая эти прямые вверх по многоугольнику решений находим вершину многоугольника, в которой целевая функция достигает максимального значения.
и так далее, -это параллельные прямые. Двигая эти прямые вверх по многоугольнику решений находим вершину многоугольника, в которой целевая функция достигает максимального значения. . Потом прямую перпендикулярную этому вектору
. Потом прямую перпендикулярную этому вектору  перемещаем по многоугольнику решений и находим вершину, , в которой целевая функция достигает максимального значения.
перемещаем по многоугольнику решений и находим вершину, , в которой целевая функция достигает максимального значения.
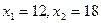 , и есть решением данной задачи ЛП. Находим максимальное значение целевой функции
, и есть решением данной задачи ЛП. Находим максимальное значение целевой функции у.е.
у.е.

 .
.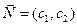 который задаёт направление возрастания значения целевой функции задачи.
который задаёт направление возрастания значения целевой функции задачи. перпендикулярную к вектору
перпендикулярную к вектору  .
.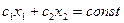 в направлении вектора
в направлении вектора