 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Некоторые алгоритмы заполнения областей
Задачи заполнения некоторой замкнутой области также называются задачами закраски. Требуется заполнить внутреннюю часть области пикселями определенного цвета. Рассмотрим 2 класса таких задач: заполнение многоугольников и заполнение области с затравкой. Для заполнения многоугольника пригоден алгоритм проверки принадлежности точки многоугольнику Но он не эффективен, т.к. требует перебора всех точек растра. Область перебора можно сократить, вписав многоугольник в прямоугольник со сторонами, параллельными осям, и рассматривая только точки этой области.
Скорость работы алгоритма можно повысить, если проверять на пересечение со сканирующей прямо не все ребра, а только те, ординаты концов которых лежат по разные стороны этой прямой (рис. б). Используется массив координат концов отрезков, образующих многоугольник, который, как правило, всегда есть. Для выпуклых многоугольников алгоритм ещё проще, т.к. есть всего 2 точки пересечения на каждой растровой прямой (рис. в). Генерируя с помощью алгоритма Брезенхема растровое представление 2 противолежащих ребер для одной и той же ординаты, получаем пикселы, лежащие на границах интервала заполнения. Задача заполнения области с затравкой формулируется следующим образом. Предполагается, что граница области задана на растровой плоскости набором символов определенного цвета и указаны координаты од ной из внутренних точек этой области. Такая точка называется затравочной. Простейший алгоритм выполняет перебор всех точек и анализ их окрестностей. Возможен анализ в рамках 4- и 8-связности. Для хранения координат точек используется стек. Сначала туда заносятся координаты затравочной точки. Извлечем из стека очередную точку, закрасим ее и исследуем ее 4- или 8-вязную окрестность. Если исследуемая точка не лежит на границе фигуры и уже не закрашена, поместим ее в стек. По окончании исследования выберем из стека очередной пиксел, повторим алгоритм. Алгоритм заполняет области любой формы. Но он неэффективен, т.к. один пиксел обрабатывается многократно, стек может неконтролируемо расти Более эффективный алгоритм основан на построчном заполнении, что позволяет обрабатывать группу пикселов. Каждую строку можно разделить на интервалы, принадлежащие или не принадлежащие закрашивав мой области. Разделитель - граница области. Если набор пикселов образует связный интервал, принадлежащий внутренней части области, то пикселы над и под этим интервалом либо являются граничными, либо принадлежат внутренней части области. Эти внутренние символы могут служить затравочными для ниже- и вышележащих строк. Целесообразно проверять на возможность использования как затравочных пикселы, лежащие под или над одной из границ найденного интервала. 23. Отсечение отрезка. Алгоритм Сазерленда-Кохена.
Задачу отсечения иногда называют задачей клиппирования (от английского clip -отрезать, отсекать). Она возникает довольно часто. Пример – размещение изобращения в окнах, в том числе занимающих весь экран, при различном разрешении (640*480, 800*600 и тд). Требуется знать пикселы, лежащие за пределами окна и не работать с ними. Решение «в лоб» – сравнивать с границами каждый выводимый пиксел. Но это долго, т.к. сравнение должно быть встроено в цикл в алгоритме Брезенхейма. К тому же границы должны или где-то храниться в виде набора адресов пикселов, или вычисляться путем 4-х кратного (для каждой стороны прямо угольника) решения уравнения прямой для каждой точки. Придется также учитывать специальные случаи горизонтальной и вертикальной прямой, а также вырождение прямой в точку. Алгоритм Сазерленда-Кохена широко известен благодаря простоте и эффективности. Плоскость делится на 9 областей. В каждой из областей точки по отношению к прямоугольнику расположены одинаково. Определив, в какие области попали концы отрезка, легко определить, где нужно отсечение. Для этого каждой облас ти сопоставляется 4-битовый код, имеющий следующий смысл:
Соотношение конечных точек и прямоугольника вычисляется с помощью поразрядных логических операции: над кодами. Они выполняются очень быстро, т.к. в процессорах 80х86 есть машинные команды AND и OR. 24. Растровое представление эллипса. Рассматриваем эллипс, т.к. это более общий случай, из него получается окружность. Если в эллипсе ориентированном вдоль осей координат, задать одинаковые горизонтальную и вертикальную координаты, окружность не получится, останется эллипс, т.к. в большинстве графических режимов вертикальный и горизонтальный масштабы различны. Точка растра имеет квадратную форму только в видеоадаптерах VGA. Для получения окружности надо рассчитать число пикселов по осям. В библиотеке BGI масштабирование уже проведено. При рисовании эллипса с одинаковыми размерами осей или окружности искажения формы нет. Для каждого графического драйвера и графического режима в BGI имеется коэффициент сжатия. Как и для прямой, координаты многих пикселов будут иметь аппроксимированное значение, фигура будет "изломанной". Как формируется эллипс? Решение "в лоб" - использовать алгебраическое уравнение. Пусть эллипс имеет координаты центра (Xс,Yс). размеры полуосей а и b, полуоси параллельны осям х и у. Вид уравнения ((X-Xc)2/ а2)+((Y-Yc) 2)/ b2)=0 Построение эллипса через уравнение, как и для прямой, нерационально по времени, т.к. вычисления по формуле громоздки, содержат долго выполняющиеся операции умножения, деления, вызов функции извлечения квадратного корня. Итерационный алгоритм для эллипса аналогичен алгоритму Брезенхема для прямой. Изображение формируется попиксельно, очередной пиксел выбирается по критерию близости к истинному значению. Т.к. эллипс симметричен относительно осей координат, достаточно иметь алгоритм формирования изображения в первом квадранте. Далее - симметричное инвертирование координат. Если эллипс не симметричен относительно осей координат, можно привести его к симметричной координатной системе поворотом осей координат. Для пересчета имеются специальные алгоритмы. Уравнение простейшего эллипса с центром в начале координат и полуосями b (по оси у) и а (по оси х): b2*x2 + а2 * y2 - а2 * b2 =0. Используется так называемый "алгоритм средней точки". Он выбирает, какой из соседних пикселов ближе к эллипсу, вычисляя, находится ли средняя между пикселями точка вне или внутри эллипса. Подставим координаты средней точки (p,q) в уравнение эллипса: d = b2 * р2 + а2 * q2 - а2 * b2. d = 0, если точка лежит на эллипсе, d<0, если точка находится внутри эллипса, d>0, если точка находится вне эллипса. Следовательно, по знаку функции можно определить ближайший пиксел.
Возникает вопрос: какую пару соседних пикселов исследовать на близость? Выбор зависит от наклона касательной к эллипсу. Пустьdу = (у2 - yl), dx = (х2 - xl). Наклон вычисляется как dy/dx. Если dy/dx > -1, выбираются соседние вертикальные пикселы. Если dy/dx < -1, выбираются соседние горизонтальные пикселы.
При dy/dx>-1 d новое=dстарое +2* b2*x старое+ b2 При dy/dx<-1 dновое=dстарое +2* a2*y старое+ a2 Т.к. в квадрате - константы, их вычисляем перед циклом один раз. В итерационном цикле изменяемая координата имеет приращение 1, поэтому вместо умножения на квадрат можно использовать сложение с вычисление вне цикла константой (квадратом). Так сложные операции умножения, деления, вычисления квадратного корн заменяются простыми операциями сложения и вычитания. Формулы для подсчета d определяются точкой, где dy/dx = -1. Как ее найти? Можно продифференцировать уравнение эллипса и приравнять результатк -1:
Инкремент для d можно вычислить:
Каждая из полученных точек сразу отображается в остальных трех квадрантах. В изображении эллипса имеются некоторые проблемы. Когда эллипс мал и для его изображения требуется сравнительно мало пикселов, аппроксимация выглядит как многоугольник (вместо плавной кривой - ломаная). Аналогична ситуациядля "тонких" эллипсов с большой разницей между а и b. Выход состоит в переходе к более высокому разрешению (может быть на том же адаптере путем сокращения количества цветов). Друга проблема - вырожденные в прямую эллипсы (а = 0 или b = 0). Здесь или dy = 0, илиdx = 0, следовательно итерация правильно не заканчивается. В программе перед циклом нужна проверка на вырождение. 25. Исходные эвристики, используемые при удалении невидимых линий и поверхностей.
Все алгоритмические поиски направлены на ускорение работы. Но зачастую весьма эффективны не сложные математические выкладки, а эвристические соображения.
1. Пусть сцена разбита на фрагменты А и В. Если самые дальние точки фрагмента А лежат ближе к наблюдателю, чем самые ближние точки фрагмента В, то никакая часть фрагмента В не может загораживать фрагмент А. Поэтому сначала строится изображение фрагмента В (дальнего), а потом - фрагмента А (ближнего). Данное эвристическое соображение устанавливает порядок обработки фрагментов изображения.
2. Пусть в пространстве объектов сцены имеется плоскость, разделяющая все пространство на 2 такие полупространства, что в одном находится фрагмент А и наблюдатель, а в другом - фрагмент В. Очевидно, что при этом фрагмент В не может загораживать фрагмент А, т.е. он должен выводиться первым. Если непересекающиеся фрагменты выпуклы, то разделяющая плоскость обязательно имеется. Если фрагменты А и В невыпуклые, можно попытаться поместить их в непересекающиеся выпуклые тела (например, шары возможно меньших диаметров). В результат получаем иной по сравнению с эвристикой №1 способ определения очередности изображения объектов.
3. Кроме порядка обработки фрагментов полезно знать, когда фрагменты могут обрабатываться независимо друг от друга. Даже при отсутствии возможности параллельных вычислений решение задачи загораживали упрощается, т.к. не требуются проверки на невидимость. Обработка фрагментов может проводиться независимо, если их проекции на картинную плоскость не пересекаются. Общая задача о пересечении проекции произвольных объектов сложна. Но есть простые частные условия не пересечения. Если вписать проекции прямоугольники со сторонами, параллельными осям координат, можно проверку не пересечения проекции заменить проверкой не пересечения прямоугольников. При этом требуется решение нескольких неравенств. Если прямоугольники не пересекаются, то вписанные в них фигуры тем более не пересекаются.
Можно придумать и другие способы установления порядка рассмотрения объектов или установления независимости. Целесообразно также сложные сцены разбивать на ряд простых и рекурсивно решать серии простых задач. Вместо сцены можно разбивать картинную плоскость и обрабатывать независимо части изображения, попадающие в соответствующие части плоскости. Способ разбиения зависит от конкретной задачи. Для невыпуклых поверхностей имеются полностью или частично видимые или невидимые грани. Если элемент видим частично, его проекция на картинную плоскость обязательно пересекается с проекцией другого ребра многогранника, через которое проходит складка проектирования. Это же - для гладких поверхностей.
26. Общее представление алгоритма удаления невидимых поверхностей. Алгоритм удаления невидимых поверхностей можно определить следующим образом: AУHЛиП = (O,S,I,f,st), где О - множество объектов в трехмерном пространстве; S - множество видимых отрезков в двумерном пространстве; I - множество "промежуточных представлений"; f - множество "функций перехода",f={PM,IS,CT,DT,VT} st - "функция стратегии". Рассмотрим смысл функций, входящих в множество f. Каждая функция перехода может иметь несколько вариантов реализации, применяемых в различных алгоритмах удаления. Т.е. каждая функция может представлять некоторый класс отображений. РМ - функция преобразования проецирования. Она строит проекции (чаще перспективные), т.е. преобразует трехмерное пространство в двумерное IS - функция вычисления точки пересечения двух графических элементов при условии, что эти элементы пересекаются только в одной точке. Элементами может быть: 2 прямые, 2 отрезка прямых, прямая и плоскость. Цель вычисления точек пересечения может быть различной: 1. Найти точку отрезка прямой, в которой происходит изменение видимости; 2. Определить, имеется ли непустое пересечение проекций 2 многоугольников на картинную плоскость (см. 3ю эвристику: при пустом пересечении возможна независимая обработка непересекающихся фрагментов); 3. Найти точки пересечения объектов со сканирующей прямой (см. растровые алгоритмы); 4. Использовать результат в тесте принадлежности (см. далее); 5. Найти точку пересечения граней объекта и прямой, соединяющей точку наблюдения со специальной тесто вой точкой в объектном пространстве. Пересекающиеся прямые описываются системой линейных уравнений: A1*x+B1*y+c1=0 Если |A1 B1| =0, прямые параллельны. A2*x+B2*y+c2=0 |A2 B2| Если a1/a2=b1/b2=c1/c2, прямые совпадают. Иначе точка пересечения имеет координаты x=(b1*c2-b2*c1)/(a1*b2-a2*b1) y=(c1*a2-c2*a1)/(a1*b2-a2*b1) Известные математические выкладки позволяют также в аналитической форме получить формулы для пересечения двух отрезков и пересечения плоскости и прямой. Для выпуклых многоугольников дело обстоит сложнее. С помощью анализа минимаксного выражения можно установить, перекрываются многоугольник или нет. Точки пересечения определяются с помощью ряда шагов, среди которых - тест пересечения.
DT - функция, выполняющая "тест глубины", т.е. сравнивающая 2 точки и определяющая, какая из них расположена дальше/ближе от точки наблюдения. Одна или обе сравниваемые точки могут принадлежать некоторой грани. Следовательно, сравниваются точка - точка, точка - грань, грань - грань. Под глубиной понимается расстояние между элементом и картинной плоскостью или между элементом и точкой наблюдения. Т.е. глубина относится к z-координате элемента, тест глубины заключается в сравнении z-координат двух элементов. Имеются 3 теста глубины: Тест DT1 применяется для объектного пространства. Тест DT2 предназначен для параллельной проекции Тест DT3 применяется в растровых алгоритмах при проверке видимости проекции граней на картинную плоскость вдоль сканирующей прямой 27. Тесты глубины, используемые при удалении невидимых поверхностей.
1. Тест DT1 применяется для объектного пространства. Он сопоставляет грань и точку и определяет, заслоняет ли грань точку Для этого ищется точка пересечения грани с так называемой "линией визирования", т.е линией, проходящей через проверяемую точку и точку наблюдения. Если пересечения нет, проверяемая точка видима. В противном случае вычисляется расстояние от точки наблюдения до точки пересеченияdp и до проверяемой точки dt. Если dp > dt, проверяемая точка видима, в противном случае - невидима.
Для проникающих граней и циклического перекрытия тест "в лоб" не работает. Поэтому грани разбивают (штриховая линия на рисунке).
3. ТестDT3 - самый простой. Он применяется в растровых алгоритмах при проверке видимости проекции граней на картинную плоскость вдоль сканирующей прямой. На сканирующей прямой выбирают интервалы, где нет пересечения проекций и нет проникающих граней в объектном пространстве. Для этих интервалов просто сравниваются z-координаты сегментов проекций. Видимый сегмент имеет наибольшую а координату и образует полоску растровой прямой. VT - функция, выполняющая "тест видимости" для данной поверхности. Она выдает значение ИСТИНА, если поверхность видима и ЛОЖЬ в противном случае. Применяется только к телам. Определяет, являете ли некоторая грань тела "передней", т.е. потенциально видимой, или "задней". Очевидно, что тест может при меняться только к структурированным объектам в объектном пространстве. К гладким поверхностям тест не применим. Если имеется несколько объектов, то тест видимости не решает вопросы загораживания. Он выявляет только заведомо невидимые элементы каждого тела. Они не участвуют в последующих вычислениях. При выполнении теста видимости сначала определяется нормаль к грани - направленный от тела век тор, перпендикулярный к грани. Уравнение нормали получается из уравнения плоскости, содержащей грань. За тем строится линия визирования -прямая, проходящая через точку наблюдения и основание нормали. Если угол между нормалью и линией визирования не превышает 2*p, грань потенциально видима. Если этот угол больше 2*p , - невидима. Видимые грани иногда называют лицевыми, невидимые - нелицевыми. Используется формулировка "потенциально видима", т.к. для невыпуклых тел или для нескольких те. нужны дополнительные тесты, проверяющие взаимное затенение. Процедура определения невидимости занимает немного времени, т.к. если найдена одна грань, затеняющая другую, то незатененную грань можно не проверять (справедливо для выпуклых тел, для невыпуклых тел тест не работает) Это позволяет сократить количество граней, участвующих в проверке на загораживание, те. существенно сократить время решения задачи Функция стратегии st определяет порядок применения функций из множества f для получения требуемого результата. Возможны 2 подхода к решению задачи и соответственно 2 типа алгоритмов: объектные и кар тинные. Объектный подход рассматривает видимость в объектном пространстве. При этом сначала выполняете. тест видимости, потом - преобразование проецирования. Временные характеристики таких алгоритмов обычно обладают квадратичной зависимостью от числа объектов сцены. Картинный подход рассматривает видимость ] пространстве отображения. Определяется видимость каждого элемента картинной плоскости (т.е. каждого пик села). При этом сначала выполняется преобразование проецирования, потом - тест видимости. Временные характеристики таких алгоритмов оцениваются как линейные функции от произведения числа объектов на число точек растра. Существуют и смешанные алгоритмы, использующие как первый, так и второй подход.
28. Основные алгоритмы удаления невидимых линий и поверхностей, их краткая характеристика и сравнительный анализ.
Задачу удаления невидимых линий и поверхностей называют также задачей загораживания. Она возникает при построении реалистических трехмерных изображений и является весьма сложной. В общем виде эта задача эффективно не решается. Наиболее критический ресурс - время. Существует множество алгоритмов удаления невидимых линий и поверхностей. В основном алгоритмы рассматривают многогранники, т.к. для изображения гладких поверхностей чаще используются полутоновые изображения и решаются задачи закраски (следующая тема). С простейшими поверхностями (в том числе гладкими можно работать с помощью аналитических представлении, Болеe сложные объекты представляют в полиэдральной форме, т.е. как совокупность многоугольников. К многоугольникам сводят и гладкие поверхности (аппроксимация, сплайны). Используют также каркасное представление, т.к. ребра многогранников образуют каркасные линии. Наиболее простыми и часто используемыми фигурами являются выпуклые многогранники. Их грани представляют собой выпуклые многоугольники. ВЫПУКЛЫЙ МНОГОУГОЛЬНИК - это плоский много угольник, обладающий следующим свойством: через каждое его ребро можно провести прямую такую, чтоВСЕвершины многоугольника, не наводящиеся на прямой, оказываются в одной полуплоскости (т.е. лежат с одной стороны от прямой). Для выпуклых многоугольников любая грань либо полностью видима, либо полностью невидима.
29. Алгоритм Робертса, алгоритм Z-буфера, метод построчного сканирования: суть, область применения, сравнительный анализ. Алгоритм Робертса Алгоритм исторически первый. Он требует, чтобы грани были выпуклыми многоугольниками. Алгоритм переборного типа. работает с ребрами, т.е. больше подходит для каркасных изображении. Ребра, смыкающие 2 невидимые грани, не рассматриваются, т.к. они 'заведомо невидимы. Каждое оставшееся ребро каждого объекта анализируется на взаимоположение со всеми гранями каждого объекта. Возможны случаи:
•грань полностью или частично закрывает ребро: • грань и ребро пересекаются Первый случай наблюдается в 2 вариантах: •ребро находится в том же полупространстве относительно грани, что и наблюдатель •ребро полностью расположено в полупространстве, не содержащем наблюдателя, но проекции грани и ребра не пересекаются и проекция ребра не содержится в проекции грани (не лежит внутри)
Во втором случае ребро полностью расположено в полупространстве, не содержащем наблюдателя. Проекция ребра полностью лежит внутри проекции грани. Если ребро полностью закрыто, оно исключается из дальнейшего рассмотрения. Для частично закрытых ребер производится разбиение, получаем видимых подребра, которые включаются в список для дальнейшего рассмотрения. В третьем случае ребро пересекается с плоскостью, содержащей грань - рис. д). Аналогично второму случаю ребро разбивается на части, из которых видимы не более 2, далее рассматриваем только видимые под ребра. Разбиение делается на 2 части по точке пересечения, рассматриваем отдельно обе части, т.е. сводим к предыдущим случаям. Если плоскость, несущая грань, и ребро пересекаются, ребро разбивается на две части по точке пересечения, каждая часть ребра рассматривается отдельно. Временные затраты алгоритма пропорциональны квадрату числа граней всех объектов. Метод Z-буфера Метод весьма прост, что делает его удобным для аппаратной реализации. Время работы не зависит с числа граней, но линейно зависит от количества точек растра и "глубины сцены", т.е. от числа граней, взаимно закрывающих друг друга. Как правило, метод используется для ортогональных проекций. Его реализация осуществляется с помощью 2 буферов: буфера глубины (Z-буфера) и буфера кадра. Буфер глубины хранит z координаты пикселов экрана (отражено в названии метода). Буфер кадра хранит информацию о состоянии пикселов экрана (интенсивность, цвет). Изначально буфер глубины инициализируется значением +бесконечность. Буфер кадра - атрибутами фона. В ходе работы проекция очередной грани объекта разлагается в растр для каждого пиксела выполняется сравнение его глубины с глубиной, ранее занесенной для этого пиксела в Z буфер. Если для нового пиксела z-координата меньше значения буфера, то он ближе к наблюдателю и, следовательно, видим. Его характеристики заносятся в буфер кадра и Z-буфер. Алгоритм легко модифицируется для получения сечений поверхности параллельными плоскостями. Для этого на экран выводятся только проекции точек с z-координатой в требуемом интервале.
Поиск по сайту: |
 Можно сделать другое улучшение. Аналогично тесту на принадлежность точки многоугольнику пересечем прямоугольник горизонталью и зафиксируем точки ее пересечения с многоугольником Пары упорядоченных в направлении оси абсцисс точек пересечения дают интервалы, лежащие внутри многоугольника. Теперь вместо одной точки можно закрасить сразу групп точек, лежащую на некоторой горизонтали внутри многоугольника. Данная схема заполнения называется заполнением в порядке сканирования строк. Алгоритм относится к типу алгоритмов построчного сканирования.
Можно сделать другое улучшение. Аналогично тесту на принадлежность точки многоугольнику пересечем прямоугольник горизонталью и зафиксируем точки ее пересечения с многоугольником Пары упорядоченных в направлении оси абсцисс точек пересечения дают интервалы, лежащие внутри многоугольника. Теперь вместо одной точки можно закрасить сразу групп точек, лежащую на некоторой горизонтали внутри многоугольника. Данная схема заполнения называется заполнением в порядке сканирования строк. Алгоритм относится к типу алгоритмов построчного сканирования.


 Очередной пиксел выбирается итеративно по отношению к предыдущему пикселу. Если dy/dx>-1х=х+1, у =у-0.5. Если dy/dx<-1, х=х+0.5, у = у -1. Сравнивая d для двух соседних точек, можно вывести итерационные формулы для d.
Очередной пиксел выбирается итеративно по отношению к предыдущему пикселу. Если dy/dx>-1х=х+1, у =у-0.5. Если dy/dx<-1, х=х+0.5, у = у -1. Сравнивая d для двух соседних точек, можно вывести итерационные формулы для d.
 Обычно алгоритм начинается в точке (0,b) и заканчивается в точке (а,0). Движение идет по часовой стрелке. Первоначально dy/dx > -1. Следовательно, выбор осуществляется между пикселями по вертикали. Затем пикселы выбираются по горизонтали до достижения оси x. Для dy/dx = -1 производится замена вертикального нахождения новой средней точки на горизонтальное.
Обычно алгоритм начинается в точке (0,b) и заканчивается в точке (а,0). Движение идет по часовой стрелке. Первоначально dy/dx > -1. Следовательно, выбор осуществляется между пикселями по вертикали. Затем пикселы выбираются по горизонтали до достижения оси x. Для dy/dx = -1 производится замена вертикального нахождения новой средней точки на горизонтальное.
 СТ - функция, выполняющая в двумерном пространстве "тест принадлежности", т.е. проверяющая, лежит ли некоторая точка внутри многоугольника. Результат - булева переменная ИСТИНА или ЛОЖЬ. Проверку на принадлежность методом подсчета числа пересечений рассматривали ранее. Есть еще один тест, известный из элементарной геометрии. Соединим прямыми исследуемую точку с каждой из вершин многоугольника. Каждая пара соседних прямых образует угол. Точка находится вне многоугольника, если сумма углов равна 0, и внутри, если эта сумма равна 2*p.
СТ - функция, выполняющая в двумерном пространстве "тест принадлежности", т.е. проверяющая, лежит ли некоторая точка внутри многоугольника. Результат - булева переменная ИСТИНА или ЛОЖЬ. Проверку на принадлежность методом подсчета числа пересечений рассматривали ранее. Есть еще один тест, известный из элементарной геометрии. Соединим прямыми исследуемую точку с каждой из вершин многоугольника. Каждая пара соседних прямых образует угол. Точка находится вне многоугольника, если сумма углов равна 0, и внутри, если эта сумма равна 2*p.
 2. Тест DT2 предназначен для параллельной проекции и оперирует элементами как в объектном пространстве так и в картинной плоскости. Проверяются либо 2 грани, либо точка и грань. Для двух граней берется некоторая точка плоскости, которая является общей для проекций на эту плоскость обеих граней. Затем находятся точки на гранях, которые проецируются в выбранную точку. Для этого координаты выбранной точки подставляются в уравнения плоскостей, содержащих грани, и эти уравнения решаются относительно координаты z (параллельная проекция, точка наблюдения находится в бесконечности и лежит на линии, расположенной перпендикулярно или под некоторым углом к плоскости проектирования). Точка плоскости выбирается так. чтобы былоzl¹z2 Считается, что грань f1 имеет приоритет над гранью f2, если zl<z2. Поэтому тест DT2 называют также приоритетным тестом. В тесте точка - поверхность пропускается шаг определения общей точки. Координаты тестируемой точки сразу подставляются в уравнение плоскости, найденная z-координата грани сравнивается с z-координатой точки, в результате решается вопрос о приоритете поверхности над точкой или наоборот.
2. Тест DT2 предназначен для параллельной проекции и оперирует элементами как в объектном пространстве так и в картинной плоскости. Проверяются либо 2 грани, либо точка и грань. Для двух граней берется некоторая точка плоскости, которая является общей для проекций на эту плоскость обеих граней. Затем находятся точки на гранях, которые проецируются в выбранную точку. Для этого координаты выбранной точки подставляются в уравнения плоскостей, содержащих грани, и эти уравнения решаются относительно координаты z (параллельная проекция, точка наблюдения находится в бесконечности и лежит на линии, расположенной перпендикулярно или под некоторым углом к плоскости проектирования). Точка плоскости выбирается так. чтобы былоzl¹z2 Считается, что грань f1 имеет приоритет над гранью f2, если zl<z2. Поэтому тест DT2 называют также приоритетным тестом. В тесте точка - поверхность пропускается шаг определения общей точки. Координаты тестируемой точки сразу подставляются в уравнение плоскости, найденная z-координата грани сравнивается с z-координатой точки, в результате решается вопрос о приоритете поверхности над точкой или наоборот.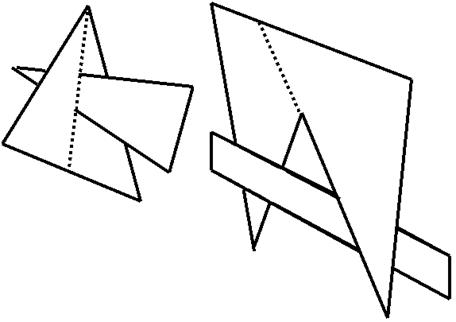
 •грань не закрывает ребро:
•грань не закрывает ребро: