 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Раскрытие неопределенности вида III
Для раскрытия неопределенности вида
1)
2)
Полученная неопределенность вида Iраскрывается по правилу Лопиталя. В первом случае правило Лопиталя применяется отдельно для неопределенности
Пример 1.
В ходе решения примера правило Лопиталя для раскрытия неопределенности вида I использовалось дважды. Один раз для раскрытия неопределенности
Пример 2.
В результате раскрытия неопределенностей вида
Раскрытие неопределенности вида IV
Для раскрытия неопределенности вида
Пример 1.
Здесь для раскрытия неопределенности вида
Пример 2. (Второй замечательный предел).
Здесь также было использовано правило Лопиталя. Пример 3.
Здесь дважды было использовано правило Лопиталя. 4. Шкала роста бесконечно больших при Рассмотрим множество степенных функций с положительным показателем степени и дополним это множество логарифмической и показательной функциями:
Все эти функции при Таким образом, начиная с логарифмической функции и кончая показательной функцией, мы имеем некую шкалу роста функций - направленное множество функций, направленность которого связана с порядком роста функций при Несмотря на то, что все функции из множества при Порядок расположения функций по шкале роста связан и продиктован справедливостью следующих предельных соотношений:
Здесь число Итак, среди всех бесконечно больших функций рассматриваемого множества «самой медленной» при Анализируя поведение функций при
Пример 1. Вычислим предел функции Сравнивая две функции под корнем, и учитывая их расположение по шкале роста, первой из них можно пренебречь по сравнению со второй. Далее сравнивая оставленную функцию о о
Поиск по сайту: |
 применяют алгебраические преобразования, сводящие неопределенность к виду I.В символической форме некоторые из них можно представить, как
применяют алгебраические преобразования, сводящие неопределенность к виду I.В символической форме некоторые из них можно представить, как ;
; .
. , во втором случае применяется ко всему искомому выражению.
, во втором случае применяется ко всему искомому выражению.


 .
.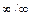 , другой раз для раскрытия неопределенности вида
, другой раз для раскрытия неопределенности вида  .
.

 .
. используется основное логарифмическое тождество
используется основное логарифмическое тождество  , а также свойство логарифма
, а также свойство логарифма  , с помощью которых функцию
, с помощью которых функцию  можно представить в виде
можно представить в виде .
.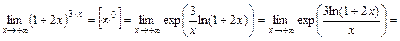
 .
. было использовано правило Лопиталя.
было использовано правило Лопиталя.
 .
.


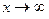 функций
функций .
.
 принимают бесконечно большие значения, но каждая из них имеет свой порядок роста (свою «скорость» роста). Порядок расположения функций во множестве соответствует их порядку роста при
принимают бесконечно большие значения, но каждая из них имеет свой порядок роста (свою «скорость» роста). Порядок расположения функций во множестве соответствует их порядку роста при 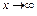 .
. 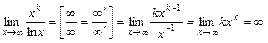 .
. 
 .
.
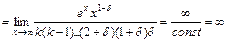 ,
, 
 является ближайшим целым числом к числу
является ближайшим целым числом к числу  . В ходе вычисления последнего предела (
. В ходе вычисления последнего предела (  ) раз применялось правило Лопиталя .
) раз применялось правило Лопиталя . , а «самой быстрой» показательная функция
, а «самой быстрой» показательная функция  .
. .
. с логарифмической функцией числителя, с учетом их расположения по шкале роста, пренебрегаем логарифмической функцией
с логарифмической функцией числителя, с учетом их расположения по шкале роста, пренебрегаем логарифмической функцией

 .
.