 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дифференциальное исчисление Функции
Нескольких переменных Основные понятия
Переменная При этом переменные
Областью определения функции Аналогично определяются функции от большего числа переменных:
Число Если Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области.
Частные производные
Пусть в некоторой области задана функция двух переменных
Оно называется частным приращением этой функции по Предел отношения
если он существует и конечен, называется частной производной функции Частную производную по
Аналогично, считая
Предел отношения
называется частной производной функции по переменной Частную производную по
Вычисление частных производных по Пример 3.1. Для функции Решение. Частные производные функции:
Полный дифференциал
Полным приращением функции
Линейная часть приращения функции Полный дифференциал функции
где При достаточно малых
Пример 3.2. Дана функция Решение. Найдем частные производные функции
Примем:
Вычислим:
Формула для приближенного вычисления с помощью дифференциала имеет вид:
Тогда
Поиск по сайту: |
 называется функцией двух переменных
называется функцией двух переменных  и
и  , если каждой паре чисел
, если каждой паре чисел  из некоторого множества по определенному правилу ставится в соответствие одно или несколько значений переменной
из некоторого множества по определенному правилу ставится в соответствие одно или несколько значений переменной 
 .
. , в которых данная функция определена. Частное (числовое) значение функции
, в которых данная функция определена. Частное (числовое) значение функции  при
при  ,
,  , обозначается:
, обозначается:  .
. .
. называется пределом функции
называется пределом функции  , если для любой последовательности точек
, если для любой последовательности точек  области определения функции, отличных от
области определения функции, отличных от  и сходящихся к
и сходящихся к  сходится к
сходится к  .
. , то функция называется непрерывной в точке
, то функция называется непрерывной в точке  в этой области и дадим
в этой области и дадим  , оставляя значение
, оставляя значение  .
. ,
, ;
;  ,
,  ;
;  .
. , получим частное приращение функции
, получим частное приращение функции  .
. ,
, ;
;  ,
,  ;
;  .
. найти значение частных производных в точке
найти значение частных производных в точке  .
. ;
;  .
. ;
;  .
. .
. или
или  .
. ,
, ,
,  .
. и
и 
 .
.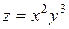 . Используя дифференциал функции, вычислить приближенно
. Используя дифференциал функции, вычислить приближенно  .
. ;
;  ;
;  .
. и
и  ;
; и
и  .
. ;
;  .
. .
. .
. .
.