 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Производные и дифференциалы высших порядков
Производной второго порядка, или просто второй производной, заданной функции Дифференцируя вторую производную, получим третью производную функции и т.д. Вообще производной
Пример 2.6.Дана функция Решение.Определяем последовательно,
Дифференциал
Пример 2.7.Дана функция Решение. Определим вначале
На основании формулы (2.5.2), получим
Исследование функций и построение графиков
Промежутки монотонности функции
Функция называется возрастающей(убывающей) в некотором промежутке, если в этом промежутке каждому большому значению аргумента соответствует большее (меньшее) значение функции. Интервалы, на которых функция возрастает (убывает), называются интервалами монотонности функции. Монотонность функции § если в некотором промежутке § если в некотором промежутке Таким образом, чтобы найти промежутки монотонности функции 1) найти нули и точки разрыва производной функции 2) определить знак Пример 2.8.Найти промежутки монотонности функции
Решение.Дифференцируя данную функцию, находим
Найдем нули и точки разрыва функции
Методом проб определим знак § на § на § на § на Таким образом, в промежутках
Экстремум функции Пусть функция Точка
Точка
Точки минимума и максимума функции называют точками экстремума. Функция Точками экстремума могут служить только точки, принадлежащие области определения функции, в которых первая производная Точками экстремума являются лишь те из критических точек, при переходе через которые первая производная Правило нахождения экстремума функции: 1. Находим первую производную. 2. Находим нули и точки разрыва 3. Определим знак производной в полученных промежутках. 4. Находим точки экстремума. 5. Находим значение функции в точках экстремума. Пример 2.9.Найти экстремум функции Решение. Функция определена на всей числовой оси. 1. Находим производную:
2. Находим нули и точки разрыва производной:
3. Точки разрыва и нули функции нанесем на числовую ось и определим знаки производной на промежутках
– 4 4. Таким образом, точки 5. Найдем значение функции в точках экстремума:
В точке Следует отметить, что точки, в которых производная обращается в ноль, иногда проще исследовать на экстремум, выяснив знак второй производной Пример 2.10. Найти экстремумы функции Решение. Область определения вся числовая ось. Найдем первую производную
Найдем нули производной
Найдем вторую производную
Найдем знак второй производной в критических точках
Таким образом,
Поиск по сайту: |
 называется производная от ее производной
называется производная от ее производной  . Для обозначения второй производной пользуются символом
. Для обозначения второй производной пользуются символом  , или
, или 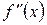 .
. -ого порядка или
-ого порядка или 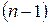 -ой производной:
-ой производной: . (2.5.1)
. (2.5.1) . Найти
. Найти  .
.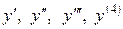 .
. ;
;  ;
;  ;
;  .
. . (2.5.2)
. (2.5.2)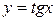 . Найти
. Найти  .
. ;
;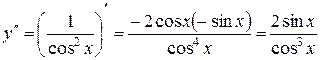 .
. .
. :
: , то функция возрастает;
, то функция возрастает; , то функция убывает.
, то функция убывает. .
. .
. .
. – не существует
– не существует  .
. Эти точки делят числовую ось на 4 промежутка:
Эти точки делят числовую ось на 4 промежутка:  ;
;  .
. 0
0 

 на каждом промежутке:
на каждом промежутке: имеем
имеем  ;
; имеем
имеем  ;
; имеем
имеем  ;
; имеем
имеем  непрерывна на некотором интервале
непрерывна на некотором интервале  , содержащем точку
, содержащем точку  .
. называется точкой максимума функции
называется точкой максимума функции  этой окрестности выполняется неравенство
этой окрестности выполняется неравенство .
. называется точкой минимума функции
называется точкой минимума функции  этой окрестности выполняется неравенство
этой окрестности выполняется неравенство .
. в положительном направлении знак
в положительном направлении знак  .
. ;
; .
. .
.
 0
0  и
и  – являются точками экстремума, причем
– являются точками экстремума, причем  – точка минимума,
– точка минимума, 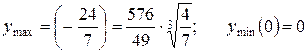 .
. экстремума нет, т.к.
экстремума нет, т.к.  (второй достаточный признак): точка
(второй достаточный признак): точка  , а
, а  существует и отлично от нуля, является экстремальной, причем точкой максимума, если
существует и отлично от нуля, является экстремальной, причем точкой максимума, если  , и точкой минимума, если
, и точкой минимума, если  .
. .
. .
. ;
; ;
; ;
; .
. .
. .
. – точки минимума,
– точки минимума,  – точка максимума. Найдем экстремумы функции
– точка максимума. Найдем экстремумы функции ;
; .
.