 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Согласно закону парности касательных напряженийСтр 1 из 29Следующая ⇒
Введение
Настоящее пособие предназначено для студентов и слушателей, изучающих дисциплину «Защита в чрезвычайных ситуациях». Оно может служить в качестве научно-методической основы при решении задач обеспечения безопасности людей и устойчивости функционирования объектов экономики в условиях чрезвычайных ситуаций, обусловленных опасными природными процессами. Для этого необходимы, прежде всего, знания физики природных катастроф и стихийных бедствий, умение определять основные поражающие факторы таких явлений, оценивать негативные последствия их воздействия на людей и объекты экономики, прогнозировать очаг поражения и оценивать обстановку в очаге поражения, знание основных мер безопасности. Под опасными природными процессами обычно подразумевают природные катастрофы и стихийные бедствия, сопровождающиеся гибелью людей и большим экономическим ущербом. К ним относят: землетрясения; оползни; обвалы; снежные лавины; вулканические извержения; наводнения на реках и морских побережьях; вихревые течения в атмосфере, приводящие к ураганным ветрам; пыльные и снежные бури; грозовые разряды-молнии; лесные, торфяные и степные пожары; массовые заболевания людей, животных и растений; падение на нашу планету космических тел и т.д. Такие катастрофы и стихийные бедствия в истории Земли отмечены неоднократно. Легенды о гибели Атлантиды, Всемирном потопе, засыпанные песками пустынь древние города Средней Азии, погребенные под слоем вулканического пепла города Помпеи, Геркулантум, Стабия в Италии – свидетельства грозных природных явлений. О масштабах потерь и человеческих трагедий можно получить представление по следующим данным. При извержении вулкана Кракатау в 1883 г., сопровождавшемся взрывом, погибло 200 тыс. человек. При землетрясении в Китае в 1923г. (провинция Нинся) погибло около 200 тыс. человек, в 1976 г. (Таншань) – 243 тыс. человек. Большую опасность представляют массовые заболевания людей. Эпидемия чумы в Европе в Х1V веке унесла 25 млн. человеческих жизней, то есть умер каждый четвертый житель этой части света, эпидемия гриппа в Западной Европе в 1918 – 1920 г. – 20 млн. жизней, то есть столько, сколько погибло в течение Первой мировой войны. По данным ООН за последние 10 лет от наводнений пострадало 150 млн. человек. Отдельно нужно остановиться на падении крупных космических тел на нашу планету. Оценено, что при падении космического тела средним размером 1 км в густо населенном районе может погибнуть до четверти населения планеты. В истории Земли случаи падения таких и более крупных тел имели место. Следует отметить, что изучение опасных природных процессов – это сложная научная задача. Она рассматривалась в ряде публикаций. Тем не менее, то обстоятельство, что отдельные вопросы рассматривались в разных работах, затрудняет изучение предмета. Кроме того, в отдельных случаях отмечается неполнота данных. Необходимо было проанализировать полученные результаты и адаптировать их применительно к требованиям дисциплины «Защита в чрезвычайных ситуациях». В пособии не ставится задача объемного изложения материала по всем вопросам, поэтому отдельные темы, которые достаточно широко освещены в имеющейся литературе, например, массовые заболевания людей, животных, растений, изложены конспективно. Более подробно рассмотрены физика землетрясений, наводнений, атмосферных вихревых движений и ряд других природных процессов, способы определения очагов поражения и оценки обстановки в очагах поражения, что потребовало привлечения отдельных положений тензорного исчисления и теории вероятностей. Изложение материала сопровождается рисунками и таблицами, содержащими необходимые справочные данные. Трудно излагать материал живо и интересно, если для его описания требуется серьезный математический аппарат. Тем не менее, попытка сделать его наглядным и удобным для усвоения в пособии предпринята. Но об этом, естественно, судить уважаемым читателям. В заключении автор выражает глубокую признательность и благодарность: Ворошнину Ю.П., Карпенко А. В., Лисицину Ю.Ф., Матвееву В. В., С.А. Печенину, Розову А. Л. за помощь в подборке литературы и критические замечания, сделанные при подготовке рукописи пособия.
Глава IЗемлетрясения.
§ 1.1 Природа землетрясений и их классификация.
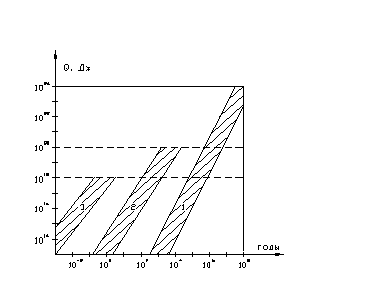
Землетрясения – грозные природные явления, с которыми связаны наиболее сильные катастрофы. При землетрясении, как правило, формируется обширный очаг поражения, на территории которого разрушаются и повреждаются здания, сооружения, техника, гибнут и получают травмы различной степени тяжести люди. Для определения очага поражения необходимо знать физические параметры землетрясения и категории поражения различных объектов. Ежегодно на нашей планете происходит порядка 100000 землетрясений, из них 100…120 способны вызвать разрушения и 10…20 оказываются достаточно сильными [1]. Землетрясения – это толчки и колебания земной поверхности, обусловленные смещением горных пород и распространением по грунтовой среде упругих сейсмических волн. По механизму образования землетрясения подразделяются на обвальные, наведенные, тектонические, вулканические и вызванные падением космических тел. Обвальные землетрясения происходят при разрушении сводов подземных карстовых пустот, заброшенных шахт, рудников, а также обвалах, сбросах горных пород. Возникающие при этом толчки и колебания земной поверхности относительно слабы. Наведенные землетрясения связаны с дополнительным давлением на земную кору, создаваемым строящимися крупными плотинами и водохранилищами, а также с изменением порового давления в грунтах при закачке воды в скважины и, наоборот, при интенсивном отборе воды с подземных горизонтов. Сильное землетрясение, вызванное заполнением водохранилища, имело место в районе расположения плотины Койна в Индии. Вскоре после начала заполнения водохранилища здесь стали ощущаться слабые толчки и колебания земной поверхности. Водохранилище было заполнено полностью к 1965 году, а в декабре 1967 года произошло землетрясение магнитудой 6.4, что соответствует энерговыделению при землетрясении ~1014 Дж. (Определение магнитуды и связь этой величины с энергией землетрясения даются в § 3). Землетрясения меньшей интенсивности наблюдались при заполнении водохранилищ у плотин Гувер и Оровилл в США, плотины Синьфын в Китае, плотины Монтэр во Франции, плотины Кремаста в Греции и в некоторых других странах [2]. Землетрясение магнитудой 5.2, что соответствует энерговыделению ~1012.7 Дж, обусловленное закачкой загрязненной отходами воды в скважину глубиной три километра, имело место в 1967 в штате Колорадо в США. И это не единственный случай. Тектонические землетрясения обусловлены движением земной коры. Наша планета имеет сложную структуру. Земная кора и верхняя часть мантии (субстрат) представляют собой твердую наружную оболочку – литосферу. Литосфера не сплошная оболочка. Она состоит из плит, средние горизонтальные размеры которых варьируются от нескольких сотен до нескольких тысяч километров. Ниже литосферы находится горячая мантия. Под действием сил, обусловленных глубинными тепловыми процессами и вращением Земли, плиты движутся со скоростью, как правило, нескольких сантиметров в год. В результате на границах литосферных плит возникают огромные механические напряжения, сопровождающиеся разрушением земных пород, – они и приводят к тектоническим землетрясениям. Тектонические землетрясения – основной тип землетрясений на нашей планете. Самые сильные из них имеют магнитуду 9.0, что соответствует энерговыделению ~1018 Дж. К числу сильнейших землетрясений ХХ века относят землетрясение у берегов Эквадора (1906 г., магнитуда 8.9) и землетрясение у берегов Японии (Санрику, 1933 г., магнитуда 8.9). Землетрясения, сопровождавшиеся большими человеческими жертвами и большим экономическим ущербом: Китай (пров. Нинся, 1920 г., магнитуда 8.6, погибло 200000 чел.), Япония (Токио, 1923 г., магнитуда 8.3, погибло 99300 чел.), Перу (Чимботе, 1970 г., магнитуда 7.8, погибло 67000 чел), Китай (Таншань, 1976 г., магнитуда 7.8, погибло 243000 чел.). Вулканические извержения могут вызвать также тяжелые последствия, примером тому являются извержения вулканов Санторин на одноименном острове в Эгейском море в 1470 году до Новой Эры, Томборо на острове Сумбава в Индонезии в 1815 году, Кракатау на одноименном острове в Зондском проливе между островами Ява и Суматра в 1883 году. Последствия этих извержений были катастрофическими. Так извержение вулкана Кракатау сопровождалось мощными взрывами, уничтожившими половину вулканического острова. В атмосферу было выброшено 19 км3 вулканической породы. Песок, пыль, обломки скал, вулканический пепел гигантским столбом поднялись на высоту до 80 км. Воздушные волны, порожденные взрывами, распространяясь со скоростью звука, трижды обогнули земной шар. Одновременно на морской акватории сформировались волны цунами высотой свыше 30 метров, поглотившие на берегах островов Явы и Суматры 36 тысяч человек. Общее число погибших от ядовитых газов, пепла, лавы, падающих вулканических бомб, камней, цунами составило ~200 тысяч человек [3]. Энерговыделение при извержении и взрыве вулкана Кракатау оценивается величиной ~1019 Дж, а вулканов Санторин и Томборо ~1020 Дж [4]. Для сравнения энергия ядерного взрыва мощностью q=106тонн, где q – тротиловый эквивалент взрыва, составляет 4,52×1015 Дж. Энерговыделение при тектонических землетрясениях ~1018 Дж и извержениях вулканов ~1020 Дж, по-видимому, составляет предел силы геологических пароксизмов на нашей планете. Размер их лимитирует прочность горных пород. Больших напряжений земная кора не выдерживает – землетрясение или вулканический взрыв снимают их. Землетрясения в результате падения космических тел хотя и представляют собой явления более редкие, но их последствия могут быть очень тяжелыми. В последнее время существование опасности падения на Землю астероидов с характерным размером 50…100 м не вызывает сомнений. Их наблюдают астрономы в обозримом с Земли пространстве на достаточно близком расстоянии, а примерно раз в 200…300 лет такие космические тела падают на нашу планету. Последнее подобное столкновение – падение Тунгусского метеорита (или фрагмента кометы) произошло в 1908 году. Характерный размер объекта составлял не более 50 м, энергия взрыва оценивается величиной ~1016 Дж. Энерговыделение при падении небесных тел с характерным размером порядка 1 км может составить величину 1020…1021 Дж. При взрыве такой мощности в густо населенных районах нашей планеты может погибнуть ~ четверть населения Земли [5]. Средний интервал времени между падением таких астероидов оценивается ~500000 лет. Еще большую опасность представляет возможное падение космических тел с характерным размером >1 км. Так энерговыделение при падении астероида, образовавшего 28 млн. лет тому назад Попигайский кратер, оценивается величиной 1023…1024 Дж. На рис. 1. приведена частота повторяемости различных природных катастроф с энерговыделением от 1013 Дж до 1023…1024 Дж [4].
на этом рисунке область 1 отвечает случаям падений метеоритов и астероидов, 2 – вулканических взрывов, 3 – тектонических землетрясений. Границы областей указывают возможный временной интервал событий. Из рисунка видно, что в среднем катастрофа с энерговыделением 1018 Дж может быть вызвана землетрясением 1 раз в год, вулканическим взрывом 1 раз в 200…300 лет, падением метеорита 1 раз в ~(50…100)×103 лет. Максимальное энерговыделение вулканической катастрофы примерно в 100 раз больше, чем при самом сильном тектоническом землетрясении, но периодичность таких событий менее 1 за 1000 лет. Астероиды, крупные метеориты могут вызвать самую сильную на Земле катастрофу, но эти события происходят ещё реже.
§ 1.2. Строение Земли. Движение земной коры. Земля имеет форму, близкую к сферической, слегка приплюснутую у полюсов, радиусом 6371 км. Наша планета не статична. Если это было бы не так, поверхность Земли давно была бы выровнена эрозией и стала плоской, а океан залил бы ее целиком. Кора, мантия, ядро – главные части Земли. Некоторое представление об ее строении можно получить по данным табл. 1. [6]. Строение Земли Таблица 1
По мере приближения к центру Земли температура, плотность вещества и давление возрастают. В центре температура составляет ~42000 С, плотность ~13×103 кг/м3, давление ~3.6×108 кПа (для сравнения, плотность стали 7.9×103 кг/м3, температура плавления 15000 С). Земная кора, гидросфера и атмосфера образовались из вещества мантии, когда-то поднявшегося к поверхности и охладившегося. Этот процесс продолжается и в настоящее время и виден, например, при извержениях вулканов, когда раскаленная лава, рождающаяся в мантии, выходит из недр.[2,6]. Как отмечалось в § 1.1, кора и верхний слой мантии «субстрат» образуют твердую земную оболочку – литосферу, состоящую из плит различных размеров. Непосредственно под литосферными плитами находится слой горячего вязкого вещества, находящегося в особом полурасплавленном (местами частично расплавленном) состоянии, называемый астеносферой (от греческого «astes» – мягкий). Под действием сил, обусловленных глубинными тепловыми процессами и вращением Земли, плиты движутся по астеносфере. Основные литосферные плиты показаны на рис. 2. [2]. Направления движения плит на этом рисунке помечены стрелками. Видно, например, что Южно-Американская плита отходит от Африканской, а Северо-Американская – от Евразиатской. Такое движение плит связано с выдавливанием расплавленного вещества из астеносферы вверх в литосферу в районе Средне-Атлантического хребта, где оно остывает и образует новую кору, то есть имеет место процесс разрастания океанического дна. В результате раздвигания медленно движущиеся плиты напирают друг на друга в других местах - при этом в зонах столкновения происходят вздымаются горные системы, возникают вулканы и острова. В разных местах плиты напирают друг на друга по-разному. Например, вдоль западного побережья Южной Америки плита Наска и Южно-Американская плита сталкиваются лоб в лоб. В результате первая из них отклоняется вниз и пододвигается под вторую. Этот процесс известен как субдукция (поддвиг). Когда одна плита пододвигается под другую, вдоль наклонной поверхности контакта плит, называемой зоной Беньоффа, происходят землетрясения. Как правило, при таком движении первая из плит стремится смять и приподнять вышележащую плиту, что также ведет к образованию горных цепей и вулканов. По мере того, как в срединно-океанических хребтах из мантии формируется новая кора, старая возвращается в мантию в зонах субдукции. Основные зоны субдукции (на рис.2. они обозначены зубчиками) расположены вдоль Алеутских островов, возле Японии, вблизи Филиппинских островов , в Индонезии, у подножья Гималаев, у западных берегов Южной и Центральной Америки и в Персидском заливе. В схематизированном виде движение земной коры показано на рис. 3.[2].
На рис. 3 толщины литосферы и астеносферы преувеличены, чтобы показать коровые структуры. В некоторых районах Земли плиты не сталкиваются, а скользят одна вдоль другой по разделяющей их границе. Наиболее известным примером такого движения является зона разлома Сан-Андреас на западной стороне Северо-Американской плиты. Время от времени землетрясения происходят и во внутренних частях плит – так называемые внутриплитовые землетрясения. Они возникают из-за развития деформаций, вызванных давлением на краях плит. Например, территория Китая сдавливается с двух сторон: с востока – Тихоокеанской плитой, с юга – Индо-Австралийской. Наиболее вероятно, что эти воздействия несут ответственность за землетрясения в Китае, включая Таншаньское в 1976 г., которое привело к гибели большого количества людей. Проведенный анализ материалов настоящего и предыдущего параграфов показывает сложную физическую картину возникновения землетрясений. Характерным признаком землетрясений, несмотря на различие природы их происхождения, является наличие системы упругих сейсмических волн, распространяющихся по грунтовой среде на большие расстояния. Сейсмические волны являются основным поражающим фактором землетрясений. Для количественного описания этой волновой системы необходимо привлечение определенных положений теории упругости.
§ 1.3. Некоторые сведения из теории упругости. Особенности напряженного состояния твердого тела.
В теории упругости материал твердого тела (таким телом может быть грунтовая среда) представляется идеально упругим. Размеры и форма такого тела полностью восстанавливаются после устранения причин, вызвавших деформацию, а между деформациями и напряжениями существует линейная зависимость (закон Гука). [7]. Деформацией твердого тела называется изменение его размеров и объема, сопровождающееся обычно изменением и его формы. Деформация вызывается внешними силовыми воздействиями или изменением температуры. При деформации происходит смещение частиц тела. Этому препятствуют силы взаимодействия между ними, вследствие чего в деформированном теле возникают внутренние упругие силы – напряжения. В строгом смысле слова напряжение – это интенсивность внутренних усилий, то есть усилие, приходящееся на единицу площади сечения тела. Напряжение называется нормальным, если упругая сила нормальна к плоскости сечения, и касательным, если она касательна к этой плоскости. Указанные напряжения часто обозначают σ и τ соответственно. Рассмотрение зависимости деформаций с напряжениями ниже вначале приводится для важных частных случаев односторонних деформаций растяжения (сжатия) и сдвига, а также случая всестороннего сжатия тела. Одностороннее или продольное растяжение (сжатие) состоит в увеличении (уменьшении) длины тела под действием растягивающей (сжимающей) силы F. Мерой деформации является относительное удлинение (сжатие) ε = Δl/l, где l – первоначальная длина тела, Δl – изменение длины при нагрузке F. По закону Гука:
где E – модуль Юнга; S – площадь поперечного сечения тела. При Δl = l модуль Юнга E = F/S = σ, то есть численно равен напряжению, возникающему в теле при увеличении его длины в два раза. Известно, что разрушение тела наступает при значительно меньших напряжениях. На рис. 4а представлена зависимость σ от ε для случая продольного растяжения тела.
Рис. 4а. Зависимость напряжения от Рис. 4б. Деформация сдвига. относительной продольной деформации.
γ
На рис. 4а обозначено: σупр – предел упругости, то есть напряжение, ниже которого справедлив закон Гука; σтек – предел текучести, то есть напряжение, при котором появляется текучесть – увеличение деформации без увеличения деформирующей силы; σпр – предел прочности - напряжение, при котором образуется местное сужение (шейка) и происходит разрушение тела (увеличение деформации даже при уменьшении деформирующей силы). Относительное продольное растяжение (сжатие) тела сопровождается его относительным поперечным сужением (расширением) Δd / d, где d – поперечный размер тела. Величина, равная отношению относительного поперечного сужения (расширения) к относительному продольному удлинению (сжатию).
называется коэффициентом Пуассона. Обычно ν < 1. Сдвигом называется деформация, при которой все плоские слои твердого тела, параллельные некоторой плоскости, смещаются параллельно друг другу. При сдвиге объем тела не меняется, рис. 4б. Сдвиг происходит под действием силы F, приложенной касательно к верхней грани; нижняя грань закреплена неподвижно. Мерой деформации является угол сдвига γ, выраженный в радианах. По закону Гука относительный сдвиг пропорционален касательному напряжению
где G – модуль сдвига. Модуль сдвига численно равен напряжению, при котором сдвиг γ = 1. Всестороннее сжатие тела под действием равномерно распределенного по его поверхности нормального напряжения σ приводит к уменьшению объема тела V на величину ΔV. Значение ΔV вычисляется по формуле
где K – модуль объемной упругости. Модуль Юнга, коэффициент Пуассона, модули сдвига и объемной упругости связаны между собой соотношениями
В общем случае под действием внешних сил в теле могут иметь место одновременно и деформации растяжения (сжатия) и сдвига; при этом напряженное состояние в рассматриваемой точке тела определяется более сложными зависимостями, чем соотношения (1.1) – (1.5), а именно тензором напряжений. Возникновение тензорного исчисления было подготовлено в XIX веке исследованиями в области дифференциальной геометрии: геометрии поверхностей (К. Гаусс) и геометрии многомерного метрического пространства (Б. Риман). Современную форму тензорному исчислению придал итальянский математик Г. Риччи- Кубастро. Идеи Риччи первоначально не получили широкого распространения. Внимание к ним возросло после появления (1915 – 1916 г.г.) общей теории относительности А. Энштейна, математическая часть которой целиком основана на тензорном исчислении. Понятие о тензоре напряжений можно получить следуя рекомендациям [7]. Пусть требуется определить напряжение на наклонной площадке (по отношению к координатной системе xyz), проходящей через точку M. Для определения искомого напряжения выделим около этой точки элементарный тетраэдр MABC, рис. 5
Рис 5. Напряжения на гранях элементарного тетраэдра. Грани MAB, MBC, MAC тетраэдра совпадают с координатными плоскостями xMy, yMz, xMz. Наклон грани ABC, параллельной заданой наклонной площадке, определяется величинами направляющих косинусов нормали nкграниABC.Обозначим косинусы углов между координатными осями x,y,z и направлением нормали n соответственно через l,m,n.
Очевидно, при стягивании элементарного тетраэдра в точку грань ABC пройдет через точку М и напряжение на ней будут соответствовать напряжениям на заданной площадке. В общем случае на тетраэдр могут действовать как объемные силы (например, сила инерции, сила тяжести), так и поверхностные – напряжения на его гранях. Пусть известные составляющие напряжений, действующих по граням, совпадающим с координатными плоскостями, но напряжение rn, действующее на наклонной грани ABC, не известно. (напряжение rn – полное напряжение). Напряжение rn можно разложить на составляющие rx, ry, rz, параллельные координатным осям. Обозначив площадь грани ABC через dF, нетрудно показать, что площади граней MBC, MAC и MAB будут соответственно равны ldF, mdF, ndF. Так как тетраэдр ABC – это бесконечно малый тетраэдр, при составлении его равновесия объемными силами как бесконечно малыми более высокого порядка, чем силы, действующие на грани, можно пренебречь. Тогда из условий равновесия тетраэдра следует
rx=sxl+txym+txzn ry=tyxl+sym+tyzn ( 1.6 ) rz=tzxl+tzym+szn
Соотношение (1.6) позволяет вычислить составляющие полного напряжения rn на наклонной площадке, проходящей через заданную точку, по известным значениям sx, sy, sz, txy, txz, tyx, tyz, tzx, tzy, составляющих напряжений в этой точке и значениям направляющих косинусов нормали к площадке l, m, n. Зная полное напряжение к этой площадке
rn=rx2+ry2+rz2 sn=rxl+rym+rzn ( 1.7 ) tn2=rn2 – sn2
Следовательно, на любой наклонной площадке, проходящей через данную точку M, нормальное и касательное напряжения могут быть выражены через известные напряжения sx, sy …. tzy или, иначе говоря, эти напряжения полностью характеризуют напряженное состояние в данной точке тела, они являются компанентами тензора напряжений. Тензор напряжений обычно предствляется матрицей вида
Tн = tyx sy tyz ( 1.8 ) tzx tzy sz
В матрице в каждой строке компоненты тензора имеют одинаковое направление, а в каждом столбце – относятся к одной и той же площадке. Нормальные напряжения располагаются по главной диагонали матрицы. Таким образом тензор напряжений – это величина, характеризующая напряженное состояние в рассматриваемой точке тела; компоненты тензора записываются в виде специальной матрицы. Необходимо отметить, что в соответствие с законом парности касательных напряжений касательные напряжения с одинаковыми индексами, действующие на двух взаимно перпендикулярных площадках, равны друг другу по величине, то – есть [7]
txy=tyx , txz=tzx , tyz=tzy. ( 1.7 )
Следовательно, с учетом закона парности касательных напряжений напряженное состояние в точке тела характеризуется шестью компонентами напряжений по координатным осям. Обычно это компоненты
sx, sy, sz, txy, tyz, tzx.
При равенстве по величине касательных напряжений (1.7) матрица (1.6) симметрицна относительно главной диагонали. Такой тензор называется симметричным. С целью упрощения письма тензор напряжений записывается часто в виде
dtik= t21 t22 t23 , i,k = 1, 2, 3, ( 1.8 ) t31 t32 t33
где t11=sx , t12=txy ….. t33=sz Итак, напряженное состояние в точке характеризуется тензором напряжений, а напряженное состояние тела – совокупность тензоров, образующее тензорное поле. Важным свойством тензора напряжений является возможность приведения его к главным осям и, как следствие, возможность определения главных напряжений. Главными называются такие площадки, на кторых касательные напряжения равны нулю. Нормальные напряжения, действующие на главных площадках, называются главными напряжениями. Пусть на наклонной площадке с нормалью n дейтсвует только нормальное напряжение sn. В этом случае полное напряжение равно нормальному, то – есть rn=sn=s, где s – главное напряжение. Составляющие полного напряжения по осям x, y, z равны rx=sl, ry=sm, rz=sn. Используя соотношение (1.6) нетрудно получить
sl=sxl+txym+txzn sm=tyxl+sym+tyzn ( 1.9 ) sn=tzxl+tzym+szn
Система однородных относительно l, m, n уравнений может быть преобразована к виду
(sx – s)l + txym + txzn = 0 tyxl + (sy – s)m + tyzn = 0 ( 1.10 ) tzxl + tzym + (sz – s)n = 0
Система (1.10) имеет отличные от нуля решения, если ее определитель равен нулю, то – есть [8]
(sx – s) txy txz tyx (sy – s) tyz = 0 ( 1.11 ) tzx tzy (sz – s)
Определитель третьего порядка (1.11) можно записать в виде
s3 – J1s2 + J2s + J3 =0, ( 1.12 )
где J1 = sx + sy + sz J2 = sxsy + sysx + szsx – txy2 – tyz2 – tzx2 J3 = sxsys + 2txytyztzx – sxtyz2 – sytzx2 – sztxy2
Корни этого кубического уравнения – искомые главные напряжения на главных площадках. Для решения уравнения (1.12) используется подстановка s = a + Тогда уравнение (1.12) принимает вид
a3 + 3ra + 2q = 0 , ( 1.14 ) где r = q = Дискриминант D = r3 + q2 уравнения (1.14) отрицателен, следовательно, все три его корня действительны. При D < 0 для решения кубического уравнения применяют так называющий тригонометрический метод [ 7,8 ]
a1 =2 где j = Для последующего определения главных напряжений s1, s2, s3 найденные значения корней a1, a2, a3 подставляются в выражение (1.13) Подставив далее каждое из напряжений s1, s2, s3 в любые два уравнения (1.10) и используя геометрическое соотношение l2 + +m2 + n2 = 1, можно определить направляющие косинусы соответствующих главных площадок. Так как для каждой точки тела имеются только три главные площадки и соответственно три главных напряжения, то эти напряжения не зависят от выбора координат и, следовательно, коэффициенты J1, J2, J3 также не зависят от выбора системы координат. Коэффициенты J1, J2, J3 называют первым, вторым и третьим инвариантами тензора напряжений. Их можно выразить через главные напряжения в виде
J1 =s1 + s2 + s3, J2 =s1s2 + s2s3+ s3s1, J3 =s1s2s3 ( 1.16 ) С тензором напряжений непосредственно связана другая величина – тензор деформаций, характеризующая состояние деформированного тела в рассматриваемой точке. [7] Тензор деформации представляет собой также симметричную матрицу, построенную из составляющих, на которые в окрестности рассматриваемой точки может быть разложена любая сложная деформация элементарного (очень малого) объема твердого тела. Если через данную точку провести координатные оси, например x, y, z, то тензор деформаций запишется в виде
TД = ½gyx eyy ½gyz , ( 1.17 ) ½gzx ½gzy ezz
где компоненты тензора выражаются через проекции смещения Wx, Wy, Wz той же точки на оси x, y, z следующим образом
exx= gxy=
Тензор деформаций записывают также в виде
e11 e12 e13 deik = e21 e22 e23 , i,k = 1, 2, 3, e31 e32 e33
где e11=exx, e12=½gxy,…e33=ezz. Тензор деформаций, как и тензор напряжений, может быть приведен к главным осям. Главными осями деформаций называются такие три взаимно ортогональные прямые, проходящие через точку тела, которые совпадают по направлению с линейными элементами, испытывающими при деформации только изменения длин. Деформации этих элементов называются главными деформациями в точке тела. Сдвиги в главных осях деформации равны нулю. Главные деформации определяются по уравнениям, аналогичным (1.10) – (1.14), при замене значений напряжения на величины соответствующих деформаций [7]. Главные деформации принято обозначать через e1, e2, e3. Инварианты тензора деформаций, выражение через главные деформации, имеют вид J1=e1+ e2+ e3; J2=e1e2+ e2e3+e3e1; J3=e1e2e3 ( 1.19 ) В дальнейшем потребуется значение некоторых правил действий с тензорами [9]. При сложении ( вычитании ) тензоров daik и dbik, где i,k = =1,2..…. n, образуется тензор dcik с компонентами cik= aik
При умножении скаляра А на тензор daik образуется тензор dсik с компонентами сik= A aik ( 1.21 )
Тензорным произведением двух тензоров daik и dbik называется тензор dсik с компонентами cik где при суммировании берутся парные произведения компонентов строк первого тензора и компонентов столбцов второго тензора с одинаковыми вторыми индексами у первых и первыми индексами у вторых сомножителей соответственно. Пример. Определить компоненты тензорного произведения dсik тензоров daik и dbik при i,k= 1, 2, 3. Решение. Значение dcik находим по формуле (1.22)
C11= a11b11 + a12b21 + a13b31 C12= a11b12 + a12b22 + a13b32 …………………………… C33= a31b13 + a32b23 + a33b33
§ 1.4. Обобщенный закон Гука В теории упругости различают изотропные и анизотропные среды. В первых из них упругие свойства среды одинаковы во всех направлениях, во вторых средах – упругие свойства различны по различным направлениям. При распространении сейсмических волн, образующихся при землетрясении, грунт обычно рассматривается как изотропная среда. В самом общем виде связь между деформациями и напряжениями в изотропной среде представляется в виде тензорного уравнения вида [7] dtik= lqdjj + mdeik; i,k=1, 2, 3; j=1, 2, 3 ( 1.23 ) где dtik – тензор напряжений; deik – тензор деформаций; djj – единичный тензор Кронекера; q – объемная деформация; m, l - упругие константы Ламе. Значения djj и q соответствуют
djj= 0 1 0 ( 1.24 ) 0 0 1
q= e11 + e22 + e33
Упругие константы Ламе l, m связаны с модулем Юнга E, коэффициентом Пуассона n и модулем сдвига G соотношениями
С учетом правил сложения тензоров и умножения скаляра на тензор компоненты тензоров (1.23) могут быть записаны в виде системы уравнений t11= l(e11 + e22 + e33) +2me11 t22= l(e11 + e22 + e33) +2me22 t33= l(e11 + e22 + e33) +2me33 ( 1.26 ) t12= 2me12 t23= 2me23 t31= 2me31
Согласно закону парности касательных напряжений t21= t12; t32= t23; t13= t31.
Соотношения (1.26) представляют собой обобщенный закон Гука. Они устанавливают связь между деформациями и напряжениями в случае сложного напряженного состояния тела. Можно показать, что в важных частных случаях одностороннего сжатия (растяжения) и сдвига они переходят в известные состояния (1.1) – (1.3). Пусть, например, имеет место одностороннее сжатие тела. При этом напряжения t11
и система уравнений (1.26) принимает вид t11= l(e11 + e22 + e33) +2me11 0 = l(e11 + e22 + e33) +2me22 0 = l(e11 + e22 + e33) +2me22 ( 1.27 ) 0 = e11 = e22 = e33 Вычитая из второго уравнения этой системы третье уравнение, нетрудно получить 2m(e22 – e33)= 0
Следовательно, деформации e22 = e33, и из второго уравнения (1.27) можно получить 0= le11 + 2le22 + 2me22
Отсюда с учетом соотношения (1.25) e22 = e33 =
Подстановка значений e22 и e33 в первое уравнение (1.27) с учетом соотношений (1.25) приводит к выражению t11=
Соотношения (1.29), (1.28) есть не что иное, как формулы (1.1) и (1.2), причем знак минус в соотношении (1.28) перед коэффициентом Пуассона n указывает, что при произвольном сжатии тела происходит увеличении его размеров в поперечном направлении и, наоборот, при растяжении в продольном направлении имеет место сужение тела в поперечном направлении. Пусть имеет место односторонний сдвиг при t12>0. В этом случае t11= t22= t33= t23= t31= 0
При сдвиге изменение объема тела не происходит. Следовательно q= e11 + e22 + e33 = 0
С учетом данных соотношений из уравнений (1.27) можно получить t12= 2me12 e11= e22= e33= e23= e31= 0
Учитывая, что e12 t12= Gg12, что полностью совпадает с формулой (1.3)
§ 1.5. Распространение колебаний в упругой среде. Распространение упругих возмущений в изотропной среде описывается уравнением Ламе [10]
где r – плотность среды (грунта); W – смещение точек среды; F – массовая сила (например, для силы тяжести F=g); l, m – упругие константы Ламе. В уравнении (1.30) величина div W – это дивергенция, то – есть расхождение векторного поля W в точке (x, y, z). Если обозначить проекции векторного поля W на координатные оси через Wx, Wy, Wz, то можно представить
Div W=
Величина graddiv W ( градиент div W) – это вектор, показывающий направление наиболее быстрого изменения div W
graddiv W где i, j, k – орты координатных осей x, y, z. Величина D в уравнении (1.30) – это оператор Лапласа
D
При распространении упругих возмущений неограниченной изотропной среде массовой силой F обычно пренебрегают по сравнению с упругими силами и силами инерции. Тогда с учетом пояснений относительно значений graddiv W и DW уравнение (1.30) можно записать в проекции на координатные оси в виде
При распространение упругих возмущений на большие расстояния движение среды можно рассматривать как плоское движение. В этом случае смещение W зависит только от одной из декартовых координат, например x, и времени t.
Обозначив
нетрудно получить
Уравнения (1.34) представляют собой волновые уравнения, где величины a, b являются скоростями распространения возмущений. Видно, что скорости распространения составляющей смещения Wx и составляющих Wy, Wz различны. Следовательно, в рассматриваемом случае движения возмущений в упругой грунтовой среде формируется волновая система, состоящая из двух волн [10]. В одной из них смещение (Wx) совпадает с направления распространения самой волны. Такая волна называется продольной и распространяется со скоростью а=
§ 1.6. Потенциальная энергия деформаций.
Потенциальная энергия деформаций численно равна работе внутренних усилий (напряжений) на перемещениях, вызванных действием этих усилий. [7] Рассмотрим, например, работу напряжения sx при деформации ex
где Е – модуль Юнга, Q* – работа напряжения. Рассмотрим далее работу напряжений sx, sy, sz, txy, tyz, tzx, действующих на гранях элементарного (бесконечно малого) объема, например, куба с ребрами dx, dy, dz, при деформациях ex, ey, ez, gxy, gyz, gzx соответственно. По аналогии с выражением (1.35) нетрудно получить [7].
Используя зависимости между деформациями и напряжениями (1.26), с учетом соотношений (1.25) можно найти
Если координатные оси x, y, z – главные оси деформации тогда gxy=gyz=gzx=txy=tyz=tzx= 0; при этом соотношение (1.37) принимает вид
где s1, s2, s3 – главные напряжения. Потенциальная энергия напряженного тела может быть определена интегрированием соотношений (1.36) – (1.38) по всему объему тела.
При землетрясении очаг землетрясения находится обычно на глубинах от нескольких километров до нескольких сот километров. На таких глубинах напряжения в грунте могут достигать больших значений. Область, занятая очагом, также может иметь значительные размеры. Указанные обстоятельства объясняют выделение большого количества энергии при землетрясении.
§ 1.7. Волновая система при землетрясении.
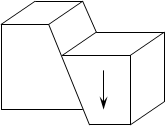
Высвобождение накапливающейся длительное время в земной коре энергии напряжений сжатия, растяжения, сдвига обычно происходит в некотором объеме, называемом очагом землетрясения. В пределах очага имеет место разрушение земных пород. В геологии используется специальный термин – разлом.[1,12] Протяженность разлома (а значит и очаговой области) может достигать десятков, в отдельных случаях – сотен километров. Образование разлома часто сопровождается смещением земных пород. Если при этом образование разлома происходит в результате действия растягивающих усилий, то некоторый объем породы может соскользнуть вниз – возникает так называемый нормальный сброс. При сжатии часть породы может быть выдавлена вверх – такой разлом называют обращенным сбросом. Возможно также горизонтальное перемещение некоторого объема породы при наличии сдвигающих усилий; в этом случае говорят о поперечном сбросе. Указанные типы сбросов поясняет рис. 6.
а) б) с)
Рис. 6. Схемы разломов при землетрясении. а – нормальный сброс, б – обращенный сброс, с – поперечный сброс.
В очаге землетрясения выделяется точка, в которой начинается разрушение земной породы, именуемая гипоцентром. Проекция гипоцентра на земную поверхность называется эпицентром. Возмущения грунтовой среды, порожденные в гипоцентре, распространяются во все стороны в виде упругих продольной (Р) и поперечной (S) сейсмических волн. Взаимодействие этих волн с поверхностью земли возбуждает поверхностную волну (R). Схема распространения волн P, S, R в случае однородного грунтового полупространства показана на рис. 7.[13]
Эпицентр Точка наблюдений
Поиск по сайту: |
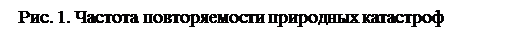



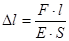 , (1.1)
, (1.1) σ
σ
 σпр
σпр








 σтек S F
σтек S F






 σупр
σупр 

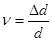 :
:  (1.2)
(1.2) , (1.3)
, (1.3) , (1.4)
, (1.4)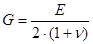 ;
;  (1.5)
(1.5)











 sx
sx txy tyx
txy tyx



 sy tzx
sy tzx
 tzy tyz txz
tzy tyz txz
 sz
sz







 J1 ( 1.13 )
J1 ( 1.13 ) J13 +
J13 +  J1J2
J1J2 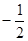 J3
J3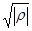 cos j , a2 =2
cos j , a2 =2  ) , a1 =2
) , a1 =2 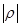 - абсолютное значение коэффициента r;
- абсолютное значение коэффициента r; arccos
arccos 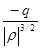
 , eyy=
, eyy= 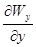 , ezz=
, ezz=  , ( 1.18 )
, ( 1.18 ) , gyz=
, gyz=  , gzx=
, gzx= 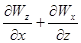

 bik ( 1.20 )
bik ( 1.20 )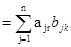 , ( 1.22 )
, ( 1.22 )

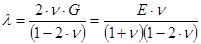
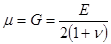 ( 1.25 )
( 1.25 ) , t22= t33= t12=t23= t31=0.
, t22= t33= t12=t23= t31=0. ( 1.28 )
( 1.28 ) ( 1.29 )
( 1.29 )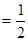 g12, m= G, где g12 – угол сдвига, G – модуль сдвига, первое из этих соотношений принимает вид
g12, m= G, где g12 – угол сдвига, G – модуль сдвига, первое из этих соотношений принимает вид ( 1.30 )
( 1.30 )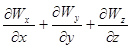
 ,
,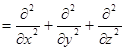
 ( 1.31 )
( 1.31 ) ( 1.32 )
( 1.32 ) ;
;  , ( 1.33 )
, ( 1.33 ) ;
;  ;
;  ( 1.34 )
( 1.34 )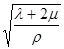 . В другой – смещение (
. В другой – смещение (  ) лежит в плоскости, ортогональной к направлению ее распространения. Такая волна называется поперечной и распространяется со скоростью
) лежит в плоскости, ортогональной к направлению ее распространения. Такая волна называется поперечной и распространяется со скоростью  .
. , ( 1.35 )
, ( 1.35 ) ( 1.36 )
( 1.36 ) (1.37)
(1.37) , ( 1.38 )
, ( 1.38 ) ( 1.39 )
( 1.39 )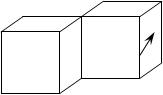



 L
L










