 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Пределы числовых последовательностей и функций.
ИЗ № 1 Образец выполнения ИЗ № 1. Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1. Решение: Данную последовательность можно представить как произведение ограниченной последовательности Тогда: 1.2. Решение:
1.3. Решение: Как и в первом пункте данного задания, представим данную последовательность в виде произведения двух последовательностей:
Задание 2. Найти пределы функций: 2.1. Решение: В данном случае имеем неопределённость вида Пусть дана дробно-рациональная функция 1. Если степень многочлена 2. Если степень многочлена 3. Если степень многочлена В данном случае степени числителя и знаменателя равны двум, поэтому 2.2. Решение: В данном случае снова имеем неопределённость вида 2.3. Решение: В данном случае снова имеем неопределённость вида 2.4. Решение: В данном случае имеем неопределённость вида
2.5. Решение: В данном случае имеем неопределённость вида
2.6. Решение: Имеем неопределённость вида
Замечание. При выполнении этого задания и заданий, подобных ему, можно использовать и другие способы решения – например, применить правило Лопиталя или эквивалентность бесконечно малых функций.
2.7. Решение: Имеем неопределённость вида
2.8. Решение: Имеем неопределённость вида
2.9. Решение: Обратим внимание, что в данном случае
2.10. Решение: Прежде всего, заметим, что если
Задание 3. Исследовать функцию на непрерывность:
Решение: Найдём область определения данной функции. Точка Точка
Окончательный ответ: функция непрерывна при
Вариант № 1.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 2.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 3.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 4.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 5.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 6.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 7.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 8.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 9.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 10.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 11.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 12.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 13.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 14.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость: 1.1.
Задание 2. Найти пределы функций: 2.1.
Задание 3. Исследовать функцию на непрерывность:
Вариант № 15.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
Задание 2. Найти пределы функций:
2.1.
Задание 3. Исследовать функцию на непрерывность:
Поиск по сайту: |
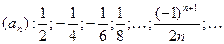
 , предел которой не определён, и сходящейся последовательности
, предел которой не определён, и сходящейся последовательности  , предел которой равен нулю. Согласно одному из свойств сходящихся последовательностей, произведение ограниченной и сходящейся последовательности есть также сходящаяся последовательность, предел которой равен пределу последней.
, предел которой равен нулю. Согласно одному из свойств сходящихся последовательностей, произведение ограниченной и сходящейся последовательности есть также сходящаяся последовательность, предел которой равен пределу последней. .
. .
. .
. .
. , где
, где  . Очевидно,
. Очевидно,  . Последовательность
. Последовательность  в силу свойств косинуса является ограниченной:
в силу свойств косинуса является ограниченной:  . Таким образом, члены последовательности
. Таким образом, члены последовательности  при
при  будут принимать как неограниченно большие, так и неограниченно малые значения. Следовательно, данная последовательность является расходящейся и предел её не определён.
будут принимать как неограниченно большие, так и неограниченно малые значения. Следовательно, данная последовательность является расходящейся и предел её не определён. .
. . Для её раскрытия используем следующее известное свойство.
. Для её раскрытия используем следующее известное свойство. , где
, где  некоторые многочлены. Тогда:
некоторые многочлены. Тогда: больше степени многочлена
больше степени многочлена  , то
, то  .
. .
. , где
, где  числовые коэффициенты при наивысших степенях
числовые коэффициенты при наивысших степенях  в данных многочленах.
в данных многочленах. .
. .
. .
. .
. . Чтобы раскрыть её, преобразуем данную функцию, предварительно разложив на множители числитель и знаменатель:
. Чтобы раскрыть её, преобразуем данную функцию, предварительно разложив на множители числитель и знаменатель:  .
. .
. . Чтобы раскрыть её, домножим данную дробь на дробь, сопряжённую её знаменателю:
. Чтобы раскрыть её, домножим данную дробь на дробь, сопряжённую её знаменателю: .
. .
. . Заметим, что
. Заметим, что  , при
, при  . Получим:
. Получим: .
. .
. .
. .
. .
. . Заметим, что
. Заметим, что 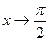 . Получим:
. Получим: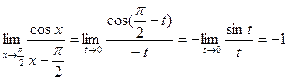 .
. .
. . Чтобы раскрыть её, приведём данную дробь к виду, который допускал бы применение второго замечательного предела
. Чтобы раскрыть её, приведём данную дробь к виду, который допускал бы применение второго замечательного предела  .
.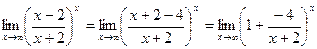 . Далее, воспользовавшись равенствами
. Далее, воспользовавшись равенствами  и
и  , получим:
, получим:  .
. .
. , поэтому нет необходимости использовать второй замечательный предел, поскольку нет никакой неопределённости, и предел может быть вычислен непосредственно.
, поэтому нет необходимости использовать второй замечательный предел, поскольку нет никакой неопределённости, и предел может быть вычислен непосредственно. .
. .
. будет принимать близкие к нулю отрицательные значения, и выражение
будет принимать близкие к нулю отрицательные значения, и выражение  , очевидно, стремится к
, очевидно, стремится к  . Тогда:
. Тогда:  .
.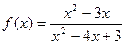 .
. . Итак, имеем две точки разрыва:
. Итак, имеем две точки разрыва: 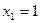 и
и 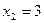 . Теперь определим, каков характер разрыва функции в каждой из этих точек.
. Теперь определим, каков характер разрыва функции в каждой из этих точек. .
.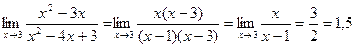 .
. ; точка
; точка  .
. . 1.2.
. 1.2.  ; 1.3.
; 1.3.  .
. . 2.2.
. 2.2.  . 2.3.
. 2.3.  . 2.4.
. 2.4.  . 2.5.
. 2.5.  . 2.6.
. 2.6.  . 2.7.
. 2.7.  . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  .
. .
. . 1.2.
. 1.2.  ; 1.3.
; 1.3.  .
. . 2.2.
. 2.2.  . 2.3.
. 2.3.  . 2.4.
. 2.4. 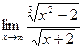 . 2.5.
. 2.5. 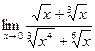 . 2.6.
. 2.6.  . 2.7.
. 2.7.  . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10. 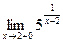 .
. .
. . 1.2.
. 1.2.  ; 1.3.
; 1.3.  .
.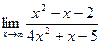 . 2.2.
. 2.2.  . 2.3.
. 2.3.  . 2.4.
. 2.4.  . 2.5.
. 2.5.  . 2.6.
. 2.6.  . 2.7.
. 2.7.  . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  .
. .
. . 1.2.
. 1.2.  ; 1.3.
; 1.3. 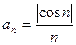 .
. . 2.2.
. 2.2.  . 2.3.
. 2.3. 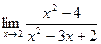 . 2.4.
. 2.4. 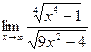 . 2.5.
. 2.5.  . 2.6.
. 2.6.  . 2.7.
. 2.7. 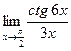 . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  .
. .
. . 1.2.
. 1.2.  ; 1.3.
; 1.3.  .
. . 2.2.
. 2.2.  . 2.3.
. 2.3.  . 2.4.
. 2.4.  . 2.5.
. 2.5.  . 2.6.
. 2.6.  . 2.7.
. 2.7.  . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  .
. .
. . 1.2.
. 1.2.  ; 1.3.
; 1.3.  .
. . 2.2.
. 2.2.  . 2.3.
. 2.3. 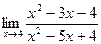 . 2.4.
. 2.4.  . 2.5.
. 2.5.  . 2.6.
. 2.6. 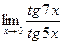 . 2.7.
. 2.7.  . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  .
. .
. . 1.2.
. 1.2. 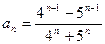 ; 1.3.
; 1.3.  .
. . 2.2.
. 2.2.  . 2.3.
. 2.3.  . 2.4.
. 2.4.  . 2.5.
. 2.5.  . 2.6.
. 2.6.  . 2.7.
. 2.7.  . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  .
.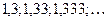 . 1.2.
. 1.2. 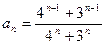 ; 1.3.
; 1.3.  .
. . 2.2.
. 2.2.  . 2.3.
. 2.3. 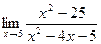 . 2.4.
. 2.4.  . 2.5.
. 2.5.  . 2.6.
. 2.6.  . 2.7.
. 2.7. 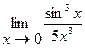 . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  .
.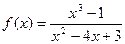 .
. . 1.2.
. 1.2.  ; 1.3.
; 1.3.  .
. . 2.2.
. 2.2.  . 2.3.
. 2.3.  . 2.5.
. 2.5.  . 2.6.
. 2.6.  . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  .
. .
. . 1.2.
. 1.2. 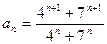 ; 1.3.
; 1.3.  .
. . 2.2.
. 2.2. 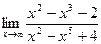 . 2.3.
. 2.3.  . 2.4.
. 2.4.  . 2.5.
. 2.5.  . 2.6.
. 2.6.  . 2.7.
. 2.7.  . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  .
. .
. . 2.6.
. 2.6.  . 2.6.
. 2.6.