 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предельное сравнение функций ⇐ ПредыдущаяСтр 5 из 5
Рассмотрим две функции Определение 13. Если
то говорят, что
Если Формула (13) означает, что
где Введем следующую терминологию. а) Если б) Если в) Если г). Если Эта терминология необходима для сокращения записи формул и упрощения вычислений. Определение 14. Функции
и записывают Например, Имеют место следующие свойства эквивалентных пределов. Теорема 19. Если □ Теорема 20. Для того, чтобы при □ Необходимость и достаточность. Теорема 21. Если
□ Докажем (17):
Теоремы говорят о том, что сомножитель (или делитель) под знаком предела может быть заменен на эквивалентный ему сомножитель (делитель). Слагаемые (т. е. в суммах и разностях) заменять на эквивалентные в общем случае нельзя. Пример 20. 1) 2)
3.7. Контрольные вопросы 1.Сформулируйте определение функции. В чем состоит однозначность? С помощью какого понятия определяется функция? 2.Что называется постоянной функцией? 3.Сформулируйте условие ограниченности функций. 4.Дайте определение точной верхней (нижней) грани функции. 5.Что означает запись 6.Что называется графиком функции? Приведите примеры функции и не функции. Дайте геометрическую интерпретацию. 7.Что, значит, задать функцию? Какие существуют способы задания функции? 8.Сформулируйте определения сложной и обратной функции. Приведите примеры. 9.Перечислите основные элементарные функции. 10.Какая функция называется элементарной? Приведите примеры. 11.Приведите пример не элементарной функции. 12.Сформулируйте определения рациональной, иррациональной и трансцендентной функций. Приведите примеры. 13.Сформулируйте два определения предела функции. Что означает эквивалентность этих определений? 14.Приведите пример функции, не имеющей предела в данной точке. 15.При каких условиях из существования односторонних пределов функции следует существование предела функции и наоборот? 16.Существует ли 17.Сформулируйте определение предела функций при 18.Докажите, что 19.Докажите первый специальный предел. 20.Докажите, что 21.Сформулируйте определение бесконечно малой функции: а) при 22. Какова связь между понятиями предела функции и бесконечно малой функцией? 23. Сформулируйте определение бесконечно большой функции: а) при 24. Что означают записи: 25. Какова связь между бесконечно малой и бесконечно большой функциями? 26. Что значит сравнить две бесконечные малые функции? 27. Приведите примеры бесконечно малой функции а) одного порядка малости с функцией б) эквивалентной функции в) более высокого порядка малости, чем 28. Что означает символическая запись 29. Докажите, что: а) 30. Верно ли равенство 31. Докажите, что 32. Верно ли равенство 33. Докажите, что 34. Сравните следующие бесконечно большие функции при а) б) в) 35. Что означают записи: 36. В каких случаях говорят о наличии неопределенности вида 37.Сформулируйте определение непрерывности функции в точке 38.В чем различие между понятиями непрерывности функции и пределом функции точке 39.Почему из непрерывности функции слева и справа в точке 40.Сформулируйте теорему об арифметических действиях над непрерывными функциями. 41.Какие точки называются точками разрыва функции? 42.Дайте определение точек разрыва первого и второго рода. 43.Укажите, в какой точке и какого рода разрыв имеет функция 44.Дайте определение сложной функции. 45.Сформулируйте теорему о непрерывности сложной функции. 46.Докажите непрерывность функции 47.Докажите, что функция 48.Почему можно утверждать, что функция 49. Сформулируйте теорему об сохранении знака непрерывной функции. 50. Можно ли утверждать, что если функция 51. Сформулируйте теорему Больцано-Коши. 52. Можно ли утверждать, что если функция 53. Сформулируйте первую теорему Вейерштрасса. 54. Может ли непрерывная на интервале функция быть ограниченной на этом интервале? 55. Может ли неограниченная на отрезке или интервале функция быть непрерывной на этих промежутках? 56. Может ли ограниченная на отрезке функция принимать значения своих точных граней? 57. Сформулируйте вторую теорему Вейерштрасса. 58. Может ли непрерывная на интервале функция достичь на этом интервале своих точных граней? 59. Дайте определение понятия равномерной непрерывности функции. 60. В чем состоит отличие понятия равномерной непрерывности от понятия непрерывности функции? 61. Сформулируйте теорему Кантора. 62. Может ли непрерывная на интервале функция быть равномерно непрерывной на этом интервале и, наоборот, равномерно непрерывная на интервале функция быть непрерывной? 63. Является ли функция 64. Приведите пример немонотонной функции. 65. Дайте определение обратной функции. 66. Сформулируйте теорему о непрерывности обратной функции. 67. Найдите функцию, обратную функции Примеры решения задач Пример 1. Найти Непосредственно теорему о пределе пределе частного применить нельзя, так как предел знаменателя при
Так как знаменатель теперь не равен нулю, то неопределенность
При вычислении пределов отношения двух многочленов при Пример 2. Найти Имеем неопределенность вида
Пример 3. Найти Имеем неопределенность вида
Пример 4. Найти Имеем неопределенность вида
так как при Пример 5. Найти Так как функция
Пример 6. Найти Имеем неопределенность вида
Таким образом,
Пример 7.Найти Имеем неопределенность вида
При Но функция
При вычислении пределов функции при Пример 8.Найти: 1) Во всех случаях имеем неопределенность вида 1) При
2) При
3) Пример 9. Найти Имеем неопределенность вида
Будем говорить, что сумма двух бесконечно больших функций разных знаков есть неопределенность вида В этом случае о пределе суммы ничего определенного сказать нельзя, так как этот предел может быть равен нулю, бесконечности, числу, отличному от нуля, а может и вовсе не существовать. Пример 10. Найти 1) 1. Имеем неопределенность вида
Теперь имеем неопределенность вида
2. Из 1) и 2), в частности, следует, что Будем говорить, что произведение бесконечно малой функции на бесконечно большую есть неопределенность вида Пример 11. Найти Имеем неопределенность вида
Получена неопределенность вида
Окончательно имеем
Поиск по сайту: |
 и
и  заданные в некоторой окрестности точки х0 , за исключением может быть самой точки х0, причем х0 конечная или бесконечная (
заданные в некоторой окрестности точки х0 , за исключением может быть самой точки х0, причем х0 конечная или бесконечная (  ). Будем считать, что
). Будем считать, что  в точке х0.
в точке х0. (13)
(13) при
при  (в окрестности точки х0) и записывают
(в окрестности точки х0) и записывают 
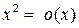 при
при 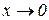
 при
при 
 , если
, если 
 при
при  .
. , то выражение
, то выражение  означает, что
означает, что  . Например,
. Например,  при
при  при
при  .
. (14)
(14)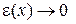 при
при  , то
, то  .
.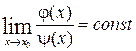 , то говорят, что
, то говорят, что  , т. е.
, т. е.  (15)
(15)
 при
при  ;
;  при
при  при
при  при
при 
 и
и  в проколотой окрестности точки х0, то можно записать
в проколотой окрестности точки х0, то можно записать  . ■
. ■ (16)
(16)

 , где
, где 
 при
при 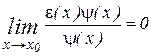 .
. при
при  (17)
(17) (18)
(18)
 , т. к.
, т. к.  .
. - верно,
- верно,  при
при  - неверно
- неверно ?
?
 .
. не существует.
не существует.
 б) при
б) при  . Приведите примеры таких функций .
. Приведите примеры таких функций .
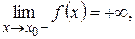

 Дайте соответствующие определения.
Дайте соответствующие определения. :
: в точке
в точке  ;
; .
. при
при  при
при 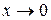 ; б)
; б) 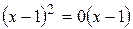 при
при  .
. при
при  ?
? при
при  .
. при
при  ?
? при
при  и
и 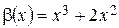 ;
; и
и  ;
; и
и  .
. ,
,  ,
,  ,
,  и
и  или
или 
 ?
? .
. .
. .
. на всей числовой прямой.
на всей числовой прямой. непрерывна в любой точке
непрерывна в любой точке  .
. непрерывна на всей числовой прямой?
непрерывна на всей числовой прямой? непрерывна в точке
непрерывна в точке  и
и  , то функция
, то функция  и на концах отрезка имеет значения одного знака, то на
и на концах отрезка имеет значения одного знака, то на  равномерно непрерывной на интервале
равномерно непрерывной на интервале  ?
?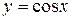 , заданной на отрезке
, заданной на отрезке 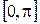 . Установите область определения, множество значений обратной функции и нарисуйте ее график.
. Установите область определения, множество значений обратной функции и нарисуйте ее график. .
. равен нулю. Здесь и предел числителя при
равен нулю. Здесь и предел числителя при  , который обращает в нуль знаменатель и числитель дроби. Это можно сделать, так как в определении предела функции при
, который обращает в нуль знаменатель и числитель дроби. Это можно сделать, так как в определении предела функции при  .
. .
. .
. .
. числитель и знаменатель дроби, а затем применив теорему об арифметических операциях над пределами, получим
числитель и знаменатель дроби, а затем применив теорему об арифметических операциях над пределами, получим
 .
. .
.
 .
.
 числитель и знаменатель дроби, получим
числитель и знаменатель дроби, получим ,
, имеет предел, равный 1, функция
имеет предел, равный 1, функция  ограниченная (докажите это самостоятельно), функция
ограниченная (докажите это самостоятельно), функция 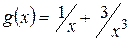 бесконечно малая (также докажите самостоятельно) и
бесконечно малая (также докажите самостоятельно) и 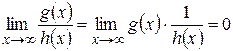 (произведение ограниченной на бесконечно малую), т. е. данная дробь, как обратная, есть бесконечно большая функция при
(произведение ограниченной на бесконечно малую), т. е. данная дробь, как обратная, есть бесконечно большая функция при  .
. , т.е. предел функции и ее значение в этой точке равны, то, переходя к пределу, получаем
, т.е. предел функции и ее значение в этой точке равны, то, переходя к пределу, получаем .
. .
. . Функция
. Функция  не определена в точке
не определена в точке  , т.е. не является непрерывной в этой точке. Поэтому сразу переходим к пределу, как в предыдущем примере, нельзя. Для нахождения предела надо функцию
, т.е. не является непрерывной в этой точке. Поэтому сразу переходим к пределу, как в предыдущем примере, нельзя. Для нахождения предела надо функцию  тождественно преобразовать так, чтобы она при
тождественно преобразовать так, чтобы она при  совпала с некоторой функцией
совпала с некоторой функцией  , непрерывной в точке
, непрерывной в точке 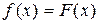 при
при  . Для этого умножим числитель дроби на сумму
. Для этого умножим числитель дроби на сумму  :
: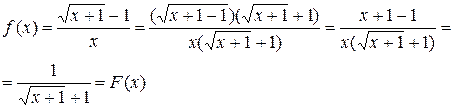 .
. , поэтому
, поэтому .
. .
. не определена в точке
не определена в точке  . Для нахождения предела преобразуем дробь:
. Для нахождения предела преобразуем дробь:
 .
. имеем
имеем  .
. непрерывна в точке
непрерывна в точке  . Поэтому, переходя к пределу, получаем
. Поэтому, переходя к пределу, получаем .
. при
при  и
и  .
. ; 2)
; 2)  ; 3)
; 3)  .
. .
.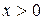 имеем
имеем  , поэтому
, поэтому
 .
. , следовательно,
, следовательно, .
. не существует, так как пределы при
не существует, так как пределы при  .
. . При
. При 
 ,
, 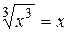 , поэтому
, поэтому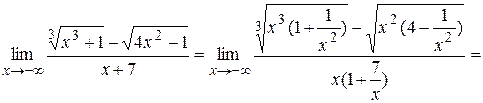
 .
. .
. ; 2)
; 2)  .
.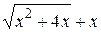 , в результате получим
, в результате получим .
. ;
; , так как сумма двух положительных бесконечно больших функций есть бесконечно большая функция (докажите самостоятельно).
, так как сумма двух положительных бесконечно больших функций есть бесконечно большая функция (докажите самостоятельно). не существует.
не существует. .
. .
. . Для нахождения предела сделаем замену переменной, положив
. Для нахождения предела сделаем замену переменной, положив 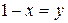 . Так как
. Так как  , то при
, то при  новая переменная
новая переменная  .Кроме того, если
.Кроме того, если  . Следовательно,
. Следовательно,

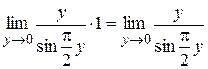 .
. . Здесь удобно воспользоваться первым специальным пределом. Для этого преобразуем дробь:
. Здесь удобно воспользоваться первым специальным пределом. Для этого преобразуем дробь: .
. .
.