 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Второй замечательный предел ⇐ ПредыдущаяСтр 3 из 3
Теорема. Пример 9.1. = = Пример 9.2. =
Определение непрерывности функции в точке Определение. Интервал Определение. Функция Определение. Функция Замечание. Неявно мы требуем, чтобы непрерывная в точке Определение непрерывности функции на множестве Определение. Функция Пример 11.1. Из рисунка 3.1 следует, что функция у= Пример 11.2.Рассмотрим график функции
Рис. 11.1 Если х>0, то Пример 11.2.На рис. 11.2 построен график
Рис. 11.2 Эта функция при Пример 11.3. Функция
Рис. 11.3 же разрывна при x=0 и непрерывна при любом Непрерывность справа (слева) Определение. Функция Аналогично определяется непрерывность слева. Пример 12.1. Все функции, графики которых указаны на рисунках 11.1, 11.2, 11.3, являются разрывными в точке х=0 как слева, так и справа.
Устранимый разрыв Определение. Функция называется разрывной в точке Определение. Функция Теорема. Если функция Пример 13.1. На рис. 11.2 мы видим функцию, которая в точке х=0 имеет устранимый разрыв. Если несколько поправить (см. рис. 13.1), то получим Рис. 13.1. непрерывную для всех х функцию
Разрыв первого рода Определение. Функция Пример 14.1. На рис. 11.1 дан график функции, которая имеет в точке х=0 разрыв первого рода, т.к. предел справа равен 1, предел слева равен -1 и эти пределы разные.
Разрыв второго рода Определение. Если разрыв не является устранимым разрывом и не является разрывом первого рода, то он называется разрывом второго рода. Пример 15.1. Функция
Поиск по сайту: |
 ,
, 
 =
=  ;Ш= =
;Ш= =  =
= 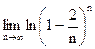 =
=  ; Ш=
; Ш=
 =
= 5=
5=  =Ш=
=Ш=  .
. =
= 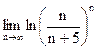 =
=  =
= 
 =
=  =Ш=-5.
=Ш=-5. , где
, где  , называется
, называется  окрестностью точки
окрестностью точки  .
. называется непрерывной в точке
называется непрерывной в точке 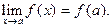

 разрывна при х=0, так как
разрывна при х=0, так как  не существует (в том смысле, что оно равняется бесконечности). Аналогично из рисунков 3.2 и 3.3 следует, что функции
не существует (в том смысле, что оно равняется бесконечности). Аналогично из рисунков 3.2 и 3.3 следует, что функции 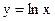 и
и 
 разрывны при х=0, соответственно при х=2. Указанные в этом примере функции непрерывны во всех точек, в которых они определены.
разрывны при х=0, соответственно при х=2. Указанные в этом примере функции непрерывны во всех точек, в которых они определены.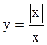 (рис.11.1):
(рис.11.1):
 Ш=
Ш=  Если х<0, то
Если х<0, то  При x=0 функция
При x=0 функция  , что и показано на рис. 11.1.
, что и показано на рис. 11.1.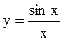 :
:
 обращается в ноль. При х, стремящегося к нулю, стремится к 1. При х=0 неопределена, что и показано на рис. 11.2. Функция разрывна при x=0 и непрерывна при
обращается в ноль. При х, стремящегося к нулю, стремится к 1. При х=0 неопределена, что и показано на рис. 11.2. Функция разрывна при x=0 и непрерывна при  (рис. 11.3) так
(рис. 11.3) так 



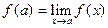 , мы получим новую функцию, непрерывную в точке
, мы получим новую функцию, непрерывную в точке 
 .
.