 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вернёмся к изложению самой сути метода Гаусса
Матрица системы
Рассмотрим специальный вид системы из трёх алгебраических уравнений
В этом случае A – верхнетреугольная матрица с единицами на главной диагонали Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений. С помощью элементарных преобразований системы уравнений получаются системы равносильные между собой. Преобразования проводятся над расширенной матрицей системы. Оказывается, над расширенной матрицей системы можно провести элементарные преобразования, после которых матрица системы будет иметь верхнетреугольный вид с единицами на главной диагонали – при этом решения исходной системы и преобразованной будут совпадать Элементарные преобразования: - строку расширенной матрицы можно поделить или умножить на число - к любой строке расширенной матрицы можно прибавить другую строку расширенной матрицы умноженную на число
(исходная система) (система с верхнетреугольной матрицей) Проведём с расширенной матрицей нашей системы элементарные преобразования (они не меняют решение системы уравнений): Прямой ход (приведение матрицы системы к верхнетреугольному виду)
=
=
(2) - ко второй строке прибавляем первую умноженную на (4) - к третьей строке прибавляем вторую умноженную на После элементарных преобразований над расширенной матрицей наша система в матричном виде выглядит так:
а в скалярном виде так:
Обратный ход (поиск неизвестных- они ищутся в обратном порядке)
Пример с числами: Решить систему из трёх алгебраических уравнений методом Гаусса:
Запишем её в матричном виде:
Её расширенная матрица имеет вид:
Поиск по сайту: |
 - исходная система
- исходная система Запишем систему в матричном виде:
Запишем систему в матричном виде: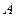 , к которой справа добавлен столбец свободных коэффициентов
, к которой справа добавлен столбец свободных коэффициентов 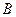 , называется расширенной матрицей системы
, называется расширенной матрицей системы 

 - расширенная матрица для нашей системы
- расширенная матрица для нашей системы эту систему решить просто (
эту систему решить просто (  - известно,
- известно,  можно найти из второго ур-я через
можно найти из второго ур-я через  из первого через
из первого через  - так выглядит рассмотренная выше система в матричном виде
- так выглядит рассмотренная выше система в матричном виде








 =
=




 =
=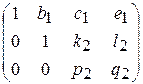


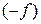 и к третьей строке прибавляем первую умноженную на
и к третьей строке прибавляем первую умноженную на  , первая строка не меняется
, первая строка не меняется , первая и вторая строки не меняются
, первая и вторая строки не меняются



 исходная система в скалярном виде
исходная система в скалярном виде
 - к матрице системы A справа добавлен столбец свободных коэффициентов
- к матрице системы A справа добавлен столбец свободных коэффициентов