 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные свойства и классификация
Основные характеристики объектов, рассматриваемых в качестве радиолокационных целей: ü отражающая способность, определяющая свойство цели переизлучать большую или меньшую долю падающей на неё электромагнитной энергии; ü закон распределения и спектр флуктуаций фазового фронта отражённого сигнала; ü закон распределения и спектр флуктуаций амплитуды (мощности) отражённого сигнала; ü особенности траектории движения. Отражающие свойства цели наряду с данными РЛС определяют её дальность действия. Отражающие свойства зависят от размеров цели, материала, из которого она выполнена, конфигурации, от длины волны РЛС и направления облучения. Практическая невозможность точного учёта всех перечисленных факторов привела к необходимости введения специальной расчётной величины – эффективной отражающей площади цели. Эффективная отражающаяплощадь цели определяется следующим образом (рис.3.1).
Рис.3.1. К определению эффективной отражающей площади цели.
Пусть РЛС создаёт у цели, находящейся на расстоянии D, плотность потока мощности rмц. Цель частично поглощает падающую на неё энергию, переизлучая остальную часть в пространство. Переизлучение происходит во многих случаях неравномерно. Чтобы не иметь дела с коэффициентом отражения и характеристиками переизлучения цели, в расчёт вводят некоторую фиктивную поверхность, имеющую площадь Sэфф. Эта поверхность не обладает поглощением и переизлучает всю падающую на неё электромагнитную энергию во все стороны с одинаковой интенсивностью. При этом величина Sэфф выбирается из условия, чтобы у приёмной антенны РЛС создавалась такая же плотность потока мощности rРЛС, как и от реальной цели. Таким образом, если цель с эффективной отражающей площадью Sэфф воспринимает мощность то у антенны станции при принятых условиях будет создана плотность потока мощности, равная Отсюда
Учитывая, что мощность пропорциональна квадрату напряжённости электромагнитного поля, получим другой вид формулы (3.1)
где xРЛС и xц - напряженности поля вблизи РЛС и цели соответственно. Эффективная отражающая площадь цели – это такая фиксированная поверхность, являющаяся изотропным и не поглощающим энергию переизлучателем, которая, будучи помещена в точку цели, создаёт у антенны РЛС такую же плотность потока мощности отражённого сигнала, как и реальная цель. Эффективная отражающая поверхность является одной из важнейших характеристик радиолокационной цели, необходимой для расчёта дальности действия РЛС. При неравномерной диаграмме переизлучения реальных целей сложной конфигурации всякое случайное или регулярное изменение ракурса их облучения со стороны РЛС приводит к флуктуациям мощности отражённого сигнала у антенны станции. Поэтому эффективная отражающая площадь таких флуктуирующих целей будет случайной величиной и может быть определена лишь статистически – законом распределения и его числовыми характеристиками. Обычно в расчётах используется среднее значение эффективной отражающей площади Sэфф0, приводимое в таблицах. Кроме закона распределения Sэфф необходимо знать также спектр её флуктуаций, чтобы правильно выбрать постоянную времени АРУ приёмника, частоту сканирования антенны при коническом обзоре и полосу пропускания следящей системы РЛС. Случайные относительные перемещения цели и РЛС приводят также к флуктуациям фазового фронта отражённого сигнала. Фазовым фронтом называется поверхность, в любой точке которой отражённый сигнал имеет одну и ту же фазу. Эффективная отражающая площадь и закон распределения, спектр её флуктуаций и спектр флуктуаций фазового фронта тесно связаны с относительным движением цели. Радиолокационные цели удобно классифицировать по методу определения их эффективной отражающей площади. С этой точки зрения все цели можно разделить на элементарные и сложные. Эффективная отражающая площадь элементарных целей может быть определена аналитически по формулам (3.1) и (3.2). Такой расчёт возможен лишь для ограниченного числа объектов простейшей формы, выполненных из однородного идеально отражающего материала. Примерами элементарных целей могут служить металлические шар, лист, вибратор, уголковые отражатели. Эффективная отражающая площадь сложных целей может быть определена только экспериментальным путём и описана статистически вследствие сложности их конфигурации и случайных перемещений относительно РЛС. К сложным целям относится подавляющее большинство реальных целей. Сложные цели, в свою очередь, могут быть разделены на точечные и распределённые. Точечные цели – это цели, линейные и угловые размеры которых значительно меньше элементов разрешения РЛСМ по дальности и угловым координатам, а разность радиальных скоростей их крайних точек много меньше элемента разрешения по скорости. Эффективная отражающая площадь точечных целей определяется экспериментально. Примерами точечной цели могут служить самолёты корабли на больших удалениях от РЛС, искусственные спутники. Распределёнными целями называют, для которых указанные выше соотношения не выполняются. Распределённые цели могут быть поверхностными (земная поверхность) и объёмными (облако пассивных отражателей, гидрометеоры). Для распределённых целей экспериментально определяется средняя удельная эффективная отражающая площадь Sэфф у. Эта величина характеризует отражающие свойства единицы площади или объёма. Полная величина Sэфф о находится из соотношений: для поверхностных целей:
для объёмных целей:
где d(S) и d(V) – размеры элементов разрешения РЛС соответственно по площади и по объёму.
Элементарные цели Элементарные цели находят практическое применение в качестве пассивных ответчиков при испытании радиолокационной аппаратуры, маскирующих отражателей при создании пассивных помех, средств имитации целей для отвлечения сил противника от действительных объектов. К элементарным целям могут быть также отнесены воздушные шары, шары – пилоты, ИСЗ простейшей геометрической конфигурации и т. д. Основными характеристиками элементарных целей являются величина их эффективной отражающей площади и ширина диаграммы переизлучения. Рассчитаем в качестве примера эффективную отражающую площадь элементарной цели в виде полуволнового вибратора. Отражатели этого типа широко применяются в массовых количествах для создания пассивных помех радиолокационным станциям. Э.д.с., наводимая в вибраторе, равна где j - угол между осью вибратора и направлением на РЛС. Ток, наводимый этой э.д.с. в вибраторе (без учёта потерь),
где RS - сопротивление излучения полуволнового вибратора, равное 73,3 Ом. Напряжённость поля, создаваемая вибратором в точке расположения РЛС, находящейся на расстоянии D, равна
Подставляя (3.5) в (3.2), получим
Полученное выражение указывает на большую зависимость эффективной отражающей площади вибратора от его ориентации относительно РЛС и от длины волны. В таблице 3.1 приведены для сравнения значения эффективной отражающей площади различных типов отражателей, имеющих одинаковые характерные размеры а, м, при длине волны облучающих колебаний l = 3 см.
Таблица3.1
Точечные цели 1. Условия, при которых цели являются точечными. Цели являются точечными, если имеют место неравенства:
где lц – наибольшей размер цели; d(D), d(jаз), d(jум), d(Vр) – разрешающие способности РЛС соответственно по дальности, угловым координатам и скорости; d(j)D = d(l) – линейная разрешающая способность по угловой координате. Таким образом, точечные цели – это такие цели, которые практически не увеличивают длительности отражённого сигнала и не изменяют его спектр по сравнению с сигналом, отражённым от цели – геометрической точки. Эти неравенства показывают также, что понятие точечной цели не является абсолютным: самолёт, например, будет точечной целью для большинства РЛС на больших расстояниях, несколько сотен метров, указанные неравенства уже не выполняются.
2. Особенности траекторий целей и их влияние на параметры РЛС. Траектория – это кривая, описываемая центром массы цели при её движении. Форма траектории может быть закономерной и случайной. Закономерными траекториями обладают баллистические ракеты, искусственные спутники. Закономерная траектория может быть однозначно определена, если измерено необходимое количество её параметров. Закономерный характер движения цели обусловливает и закономерность изменения параметров принимаемых отражённых сигналов. Это обстоятельство является весьма важным, так как оно допускает длительное накопление энергии принимаемых сигналов. Такое накопление энергии большого количества отражённых сигналов, каждый из которых несёт малую энергию, позволяет при прочих равных условиях обеспечить очень большую дальность обнаружения и высокую точность измерения параметров траектории движущихся целей. Однако при обнаружении целей, имеющих случайные траектории, нельзя использовать длительное накопление энергии принимаемых сигналов для увеличения дальности обнаружения, так как изменение их параметров не имеет закономерного характера на больших интервалах времени. Эффективное накопление в таких случаях может быть осуществлено лишь за время облучения цели сканирующим лучом антенны. Случайность траекторий маневрирующих целей требует определение характеристик обзора пространства радиолокационной станцией. Чем быстрее маневрирует цель, тем чаще должно производиться её облучение и измерение координат, для того чтобы можно было точно воспроизвести траекторию её движения. Траектория представляет непрерывную пространственно – временную функцию S(t) (рис.3.2), которая может быть задана совокупностью зависимостей D(t), jаз(t) и jум(t), выражающих полярные координаты цели как функции времени. За интервал наблюдения Тн каждая из этих функций может быть описана конечным числом дискретных отсчётов. Число этих отсчётов может быть определено по теореме Котельникова: где FВ – наивысшая частота спектра воспроизводимой функции.
Рис.3.2. Траектория маневрирующей цели.
Следовательно, конкретная траектория цели может быть воспроизведена, если период обзора РЛС будет удовлетворять неравенству причём FВ – это наиболее высокая частота из определённых по спектрам функций D(t), jаз(t) и jум(t). Так как различных траекторий может быть бесчисленное множество, а обзор проще осуществлять с постоянной скоростью, то при выборе периода обзора следует ориентироваться на самую неблагоприятную траекторию, для которой спектры функций D(t), jаз(t) и jум(t) наиболее широкие.
3.Особенности движения целей вокруг центра массы и их влияние на характер отражённого сигнала. Случайные колебания цели относительно центра массы происходят вследствие возмущений в окружающей среде и в системе управления полётом. Баллистические ракеты и искусственные спутники в полёте испытывают случайные колебания и вращения вокруг осей, случайно меняющих своё направление («кувыркаются») с «периодом» от нескольких минут до нескольких десятков минут. Случайные рыскания, продольные и поперечные крены самолётов по результатам многочисленных экспериментальных исследований имеют среднее значение амплитуды колебаний около 1-20 и средний «период» в несколько секунд. Однако для различных типов самолётов эти данные могут значительно расходиться и, кроме того, на них в сильно степени влияет состояние атмосферы. Поэтому приведённые величины следует рассматривать как весьма ориентировочные. В первом приближении моделью сложной цели, такой, как самолёт, может служить цель, состоящая из двух стабильно отражающих точек 1и 2, расположенных на расстоянии lц, равном размеру самолёта (рис.3.3).
Рис.3.3. Модель цели, состоящая из двух точек.
Оценим характер переизлучения такой цели. Для этого надо сначала определить напряженность поля результирующего сигнала в отдалённой точке В, находящейся на расстоянии D от центра О цели (D³lц). Сигнал, пришедший от точки 1, имеет вид
Сигнал, пришедший от точки 2:
Если бы существовал только один изотропный источник излучения в точке О, то сигнал от него в точке В имел бы вид
Таким образом, сигнал, пришедший от точки 1, отстаёт по фазе на угол
от сигнала е0, а сигнал от точки 2 опережает его на такой же угол (рис.3.4).
Рис.3.4. Векторная диаграмма сигналов, отражённых от точек 1 и 2 цели рис. 3.3.
Нетрудно видеть, что амплитуда результирующего сигнала
а фазовый сдвиг по отношению к сигналу е0 равен
Таким образом, результирующий сигнал, принятый от точек 1 и 2, имеет вид:
Выражение (3.12) показывает, что при Е1=Е2=Е0 амплитуда результирующего сигнала при измени направления облучения может изменяться от нуля (при
или
Считая приближённо sinj»j, получим ширину «лепестка» равной
Принимая l=3см, lц=10м, находим
При l=10см В реальных условиях при случайных движениях цели относительно центра массы и при её манёврах амплитуда отражённого сигнала будет случайной функцией времени с резкими изменениями, доходящими до нескольких десятков децибел. Закон распределения амплитуд сигналов, отражённых от различных сложных целей (самолёта, корабля, облака искусственных отражателей), по результатам различных экспериментов хорошо совпадает с распределением Релея:
где s2и – дисперсия амплитуды сигналов.
4. Эффективная отражающая площадь. Определим эффективную отражающую площадь двухточечной цели (рис.3.3). Мощность отражённого сигнала на входе приёмника:
где SА – эффективная площадь раскрыва антенны РЛС; rмРЛС – плотность потока мощности. Таким образом, при k=const мощность отражённого сигнала будет прямо пропорциональна эффективной отражающей площади цели. Мощность отражённого сигнала, в свою очередь, пропорциональна квадрату напряженности поля. Полагая, что амплитуды напряжённости поля, переизлучаемого точками 1 и 2, одинаковы и равны Е0, будем иметь
Отсюда мощность отражённого сигнала
и
где Sэфф1 – эффективная отражающая площадь каждого излучателя. Следовательно, при изменении угла y величина Sэфф может колебаться в пределах (0¸4)Sэфф1. Считая все значения y равновероятными в интервале 0¸2p, получим среднее значение эффективной отражающей площади двухточечной цели:
Перейдём теперь к определению закона распределения эффективной отражающей площади сложной цели. Мощность и амплитуда отражённого сигнала на входе приёмника связаны соотношением
где Rвх – входное сопротивление приёмника. Принимая для простоты Rвх=1, получим
Считая, что распределение амплитуды отражённого сигнала подчиняется закону распределения Релея (3.19), найдем закон распределения мощности, а, следовательно, и эффективной отражающей площади. Используем для этого формулу функционального преобразования законов распределения:
Учитывая, что
Учитывая также, что
и подставляя (3.25) и (3.26) в (3.24), будем иметь
Переходя от мощности к пропорциональной ей величине отражающей эффективной отражающей поверхности, получим окончательное выражение для плотности распределения
Обычно интересуются вероятностью того, что случайное значение будет не меньше выбранной расчётной величины Sэфф р. Интегрируя (3.28) в пределах от Sэфф р до ¥, получим
Отметим, что среднему значению эффективной отражающей площади соответствует вероятность W(Sэфф ³ Sэфф0)=0,37. Именно это значениеSэфф0 и используется в расчётах дальности действия РЛС. 5. Спектр флюктуаций амплитуды. Ширина спектра амплитудных флюктуаций цели в основном определяется степенью изрезанности диаграммы переизлучения и скоростью изменения ракурса облучения. Чем уже лепестки диаграммы и чем больше указанная скорость, тем выше частота флюктуаций. Ширина лепестков q0достигает в сантиметровом диапазоне (0,1 – 0,05)0 . Скорость изменения ракурса при маневрах самолётов может иметь величину w = 10¸20 град/сек. Таким образом, при грубой оценке антенна РЛС за одну секунду примет При рысканиях и случайных кренах самолёта скорость изменения ракурса составляет 1-2 град/сек, и частота флюктуаций, соответствующая этим движениям цели, лежит в пределах
Эта оценка хорошо согласуется с экспериментальными данными. На рис.3.5, а показан типичный спектр амплитудных флюктуаций сигнала, отражённого от неманеврирующего самолёта, на рис.3.5,б– соответствующая этому спектру корреляционная функция. Видно, что флюктуации наиболее интенсивны в области частот 0-10 Гц, а время корреляции составляет 0,05 сек. Следует заметить, что при малых дальностях в сантиметровом диапазоне волн флюктуации могут создаваться также вследствие биений сигналов, отражённых от различных точек цели, имеющих по отношению к РЛС различные радиальные скорости, а, следовательно, отражающих сигналы с различными доплеровскими смещениями частоты.
а) б) Рис.3.5.Спектр флюктуаций амплитуды и корреляционная функция сигнала, отражённого от самолёта.
Флюктуации амплитуды отражённого сигнала являются одним из основных источников ошибок в РЛС с автоматическим измерением угловых координат путём последовательно сравнения амплитуд (конический обзор). В такой системе автосопровождения для выделения сигнала ошибки используется узкополосный фильтр с резонансной частотой равной частоте сканирования. Поэтому частоту сканирования выбирают в области меньших интенсивностей флюктуаций – от 40 Гц и выше. Радикальным методом борьбы с ошибками, вызываемыми флюктуациями амплитуды сигнала, является применение моноимпульсных пеленгаторов, в которых осуществляется одновременное сравнение амплитуд, исключающее указанные ошибки. Характер изменения интенсивности амплитудных флюктуаций по частоте учитывается также при выборе постоянной времени АРУ в системах автосопровождения цели.
6. Флюктуации фазового фронта отражённого сигнала. Было замечено, что с уменьшением расстояния до сложной цели ошибки сопровождения по угловым координатам растут. Причиной этого являются флюктуации фазового фронта отражённого сигнала. Для точечного изотропного излучателя фазовой фронт представляет сферу. Поэтому пеленгация точечного изотропного излучателя при прочих идеальных условиях всегда будет осуществляться без ошибки. При пеленгации сложной цели пеленгатор при тех же условиях будет в каждый момент указывать положение нормали к фазовому фронту, не проходящей в общем случае через центр цели. При случайных перемещениях цели относительно РЛС положение нормали будет также случайным образом меняться и цель в этих условиях может быть заменена точкой, блуждающей в некотором объёме, размеры которого могут превосходить размеры цели. Эту блуждающую точку называют эффективным центром отражения цели. Таким образом, пеленгатор в некоторых случаях может указывать направление, выходящее за пределы контура цели. Обратимся снова к простейшей модели реальной цели в виде двух изотропных переизлучателей с базой lц (рис.3.3) и найдём для неё уравнение эквифазной поверхности и ошибку пеленгации. Уравнение эквифазной поверхности можно получить, если поставить условие, чтобы фаза для фиксированного момента времени оставалась постоянной:
Из этого уравнения могут быть найдены пары значений j и D, определяющие каждую точку эквифазной поверхности в зависимости от соотношения амплитуд сигналов. Выражение для ошибки пеленга при фиксированном значение угла j (рис.3.3) может быть найдено следующим образом. Производная dD/dj в какой-либо точке (j, D) поверхности определяет искривление фазового фронта двухточечной цели по сравнению со сферой, проходящей через эту же точку. Угол Dj между нормалью к поверхности в точке (j, D) и радиус-вектором D, проходящим через эту же точку, и является ошибкой пеленгации. Тангенс этого угла, как это видно из рис.3.3, равен
Выражение (3.32) показывает, что ошибка пеленгации Dj уменьшается с увеличением расстояния до цели. Это ясно и из физических соображений; если приближённо принять наибольшую амплитуду блужданий эффективного центра отражения равной размеру цели lц, то угловая ошибка при этом будет обратно пропорциональна дальности цели
При движении реальной цели угол j случайным образом меняется и ошибка флюктуирует. Это проявляется в виде случайных изменений сигнала ошибки измерения угла цели на выходе приёмника, что дало основание назвать флюктуации фазового фронта угловыми шумами цели.
7.Флюктуации времени запаздывания отражённого сигнала (флюктуации дальности) Блуждание эффективного центра отражения происходит в пределах некоторого объёма, заключающего реальную цель. Поэтому кроме флюктуаций по угловым координатам возникают также флюктуации времени прихода сигнала. Соответствующие им отклонения по дальности обычно не превышают геометрических размеров цели в направлении облучения. Спектр этих флюктуаций и плотность распределения их амплитуд весьма близко совпадают с соответствующими характеристиками угловых шумов. Величина среднеквадратического отклонения от среднего значения дальности составляет около 0,8 размера цели.
Поиск по сайту: |


 ,
, .
.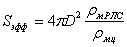 .
.
 ,
,


 ,
, - действующая высота полуволнового вибратора;
- действующая высота полуволнового вибратора; ,
,






 ,
,  ,
,
 ,
,  ,
,
 ,
,

 ,
,

 .
.
 .
.
 .
.




 .
.
 .
.
 ) до 2Е0 (при
) до 2Е0 (при  ). Ширина «лепестка» диаграммы переизлучения по «нулям» может быть найдена из условия
). Ширина «лепестка» диаграммы переизлучения по «нулям» может быть найдена из условия
 .
.
 .
.
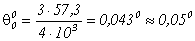 .
.
 . Таким образом, диаграмма переизлучения рассмотренной цели является весьма «изрезанной», состоящей из множества узких лепестков.
. Таким образом, диаграмма переизлучения рассмотренной цели является весьма «изрезанной», состоящей из множества узких лепестков. ,
,

 .
.

 ,
,
 .
.
 ,
,
 .
.
 .
.
 и дисперсия амплитуды есть средняя мощность флюктуирующего отражённого сигнала
и дисперсия амплитуды есть средняя мощность флюктуирующего отражённого сигнала 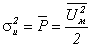 , получим
, получим .
.
 ,
,
 .
.
 .
.
 .
.
 «периодов» колебаний сигнала, что и определяет наивысшую частоту спектра флюктуаций Fфл1 =100¸400 Гц.
«периодов» колебаний сигнала, что и определяет наивысшую частоту спектра флюктуаций Fфл1 =100¸400 Гц. Гц.
Гц.

 .
.
 .
.
 .
.