 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПЛОСКОСТИ В ПРОСТРАНСТВЕСтр 1 из 3Следующая ⇒
Содержание
Введение............................................................................................. 2 1. Плоскости в пространстве 1.1. Уравнения плоскости ...................................................................... 4 1.2. Расположение плоскости относительно системы координат.......... 7 1.3. Расположение точек относительно плоскости.............................. 11 1.4. Взаимное расположение двух плоскостей.................................... 12 1.5. Расстояние от точки до плоскости................................................. 13 1.6. Расстояние между параллельными плоскостями.......................... 14 1.7. Угол между плоскостями............................................................... 15 2. Прямые в пространстве 2.1. Уравнения прямой......................................................................... 16 2.2. Взаимное расположение прямой и плоскости.............................. 20 2.3. Взаимное расположение двух прямых......................................... 21 2.4. Расстояние от точки до прямой..................................................... 23 2.5. Расстояние от прямой до плоскости, которой она параллельна. 23 2.6. Угол между прямой и плоскостью................................................ 24 2.7. Угол между двумя прямыми......................................................... 25 2.8. Расстояние между двумя параллельными прямыми.................... 25 2.9. Расстояние между двумя скрещивающимися прямыми............... 26 3. Индивидуальная работа.................................................................. 27
Введение В данных методических указаниях рассматриваются аффинная и метрическая теории прямых и плоскостей в пространстве. Аффинную теорию составляют задачи, связанные с изучением принадлежности и взаимного расположения точек, прямых и плоскостей в пространстве. Напомним, что аффинной системой координат в пространстве называется совокупность, состоящая из точки O – начало координат и тройки линейно независимых координатных векторов
Пишут: В метрической теории плоскостей и прямых в пространстве изучаются вопросы, связанные с вычислением расстояний, длин, углов, площадей и объемов. При этом приходится использовать скалярное, векторное и смешанное произведения векторов, которые наиболее просто вычисляются в ортонормированном базисе
Для векторов скалярное произведение векторов
длина вектора
Угол между векторами
Векторное и смешанное произведения
В силу сказанного, при изучении метрической теории удобней пользоваться прямоугольной декартовой системой координат
ПЛОСКОСТИ В ПРОСТРАНСТВЕ Уравнения плоскости 1. Уравнение плоскости, проходящей через данную точку параллельно двум данным векторам. Пусть
Рис. 1
Пусть в аффинной системе координат
Условие линейной независимости /неколлинеарности/ векторов
Уравнение плоскости
где,
Уравнения (2’) называются параметрическими уравнениями плоскости Условие компланарности (1) векторов виде равенства нулю их смешанного произведения:
Так как
Уравнение (4) будем называть основным. Это уравнение можно переписать в следующем виде:
где
и в силу (1)хотя бы одно из чисел
Поиск по сайту: |
 . Всякая точка М пространства, в котором задана аффинная система координат, однозначно определяется своими координатами относительно этой системы координат. При этом координатами точки М в системе координат
. Всякая точка М пространства, в котором задана аффинная система координат, однозначно определяется своими координатами относительно этой системы координат. При этом координатами точки М в системе координат 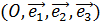 называются координаты
называются координаты 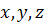 вектора
вектора 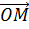 в базисе
в базисе  :
:
 .
. . Напомним, что базис векторного пространства называется ортонормированным, если его векторы имеют единичную длину и попарно ортогональны:
. Напомним, что базис векторного пространства называется ортонормированным, если его векторы имеют единичную длину и попарно ортогональны:



 заданных своими координатами в этом базисе:
заданных своими координатами в этом базисе: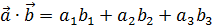

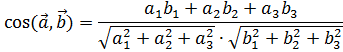
 ,
, 
 , которая является частным случаем аффинной системы координат. Наконец, напомним, что расстояние между двумя точками
, которая является частным случаем аффинной системы координат. Наконец, напомним, что расстояние между двумя точками  и
и  пространства, заданными своими координатами в такой системе, вычисляется по формуле:
пространства, заданными своими координатами в такой системе, вычисляется по формуле:
 - некоторая плоскость в пространстве. Множество векторов, параллельных плоскости α, образуют двумерное векторное подпространство L, которое называется направляющим подпространством плоскости
- некоторая плоскость в пространстве. Множество векторов, параллельных плоскости α, образуют двумерное векторное подпространство L, которое называется направляющим подпространством плоскости  и
и  образуют базис подпространства L, то для того, чтобы задать произвольную точку М плоскости
образуют базис подпространства L, то для того, чтобы задать произвольную точку М плоскости 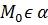 . В самом деле,
. В самом деле,  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы компланарны
компланарны
 ;
;  ;
; 
 (1)
(1) можно записать так:
можно записать так: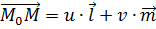 (2)
(2) или, в координатах
или, в координатах (2’)
(2’) – координаты текущей точки
– координаты текущей точки  плоскости;
плоскости;  параметры.
параметры. ,
,  ,
,  можно записать и в
можно записать и в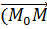 ,
,  (3)
(3) , то уравнение плоскости
, то уравнение плоскости  (4)
(4)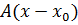 +
+  +
+  =0 (5)
=0 (5)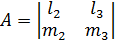 ,
,  ,
,  (6)
(6)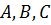 отлично от нуля.
отлично от нуля.