 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задачи для самостоятельного решения. Аналитическая геометрия на плоскости
Аналитическая геометрия на плоскости Пример 1.Построить прямые: а) Решение. а) Для построения прямой достаточно знать координаты двух ее произвольных точек. Полагая в уравнении
Получим точки
б) Прямая
в) Разрешим уравнение относительно г) Запишем уравнение в виде
Пример 2.Уравнение прямой Решение. Для получения уравнения прямой с угловым коэффициентом разрешим заданное уравнение относительно Для получения уравнения в отрезках на осях координат перенесем свободный член
Пример 3.Составить уравнение прямой, проходящей через точку а) под углом 1350 к оси б) параллельно оси в) перпендикулярно вектору г) и точку Решение. а) Будем искать уравнение прямой с угловым коэффициентом, т.е. уравнение вида (4.6). По условию б) Уравнение прямой, проходящей через точку в) Чтобы записать уравнение прямой, заданной точкой
г) Используем уравнение (4.3). Полагая
Пример 4.Найти уравнение прямой, проходящей через точку а) параллельно прямой б) перпендикулярно этой же прямой.
Решение. Будем искать уравнение прямой в виде а) Если прямая параллельна прямой б) Если прямая перпендикулярна прямой Пример 5. Найти расстояние от точки пересечения двух прямых Решение. Найдем точку
По формуле (4.11) находим расстояние
Пример 6.Даны вершины треугольника а) стороны б) медианы, проведенной из вершины в) высоты, опущенной из вершины Решение. а) Уравнение стороны
б) Чтобы составить уравнение медианы
т.е. По формуле (4.3)
в) Высота
Угол между медианой
Угловой коэффициент высоты Пример 6.Построить множество решений неравенства Решение. Множество решений линейного неравенства с двумя переменными
Если неравенство выполняется в контрольной точке, то оно выполняется и во всех точках полуплоскости, содержащей контрольную точку, и не выполняется во всех точках другой полуплоскости. И, наоборот, в случае невыполнения неравенства в контрольной точке, оно не выполняется во всех точках полуплоскости, содержащей контрольную точку, и выполняется во всех точках другой полуплоскости. В качестве контрольной точки удобно взять начало координат Задачи для самостоятельного решения 1.Написать уравнение прямой, проходящей через точку 2.Какой угол образует с положительным направлением оси абсцисс прямая
3.Определить при каком значении а) параллельна оси б) проходит через начало координат?
4. Найти угловой коэффициент прямой и ординату точки ее пересечения с осью
5. Прямая проходит через точки
6.Найти уравнение прямой: а) образующей с осью б) параллельной оси в) отсекающей на осях координат отрезки, равные 3 и 4.
7. Дана прямая а) параллельно данной прямой; б) перпендикулярно данной прямой.
8. Составить уравнение прямой, проходящую через точку пересечения прямых
9. Составить уравнение перпендикуляра к прямой
10. Найти угол между прямыми а) б) в)
11. Найти расстояние от точки
12. Показать, что прямые
13. Найти длину высоты Ответы
Поиск по сайту: |
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. , получим
, получим  . Точка
. Точка  лежит на прямой. Полагая
лежит на прямой. Полагая  , получим
, получим  . Вторая точка
. Вторая точка  . Проводим прямую
. Проводим прямую  (рис. 4.1).
(рис. 4.1).





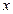


 ;
;  ;
;  .
На оси
.
На оси  отложим 2 единицы вправо от точки
отложим 2 единицы вправо от точки  . На оси
. На оси  отложим 6 единиц вниз.
отложим 6 единиц вниз.
 и
и 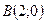 на осях, через которые проведем прямую.
на осях, через которые проведем прямую.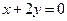 проходит через точку
проходит через точку 



 , получаем
, получаем  ,
,  . Точка
. Точка  лежит на прямой. Проводим прямую через точки
лежит на прямой. Проводим прямую через точки  . Это прямая, параллельная оси
. Это прямая, параллельная оси  .
. . Эта прямая параллельна оси
. Эта прямая параллельна оси  представить в различных видах (с угловым коэффициентом, в отрезках).
представить в различных видах (с угловым коэффициентом, в отрезках). ,
,  - уравнение прямой с угловым коэффициентом: здесь
- уравнение прямой с угловым коэффициентом: здесь  ;
;  .
.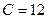 в правую часть и разделим обе части уравнения на (-12). Получим
в правую часть и разделим обе части уравнения на (-12). Получим  ,
, 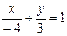 - уравнение в отрезках: здесь
- уравнение в отрезках: здесь  ;
;  .
.
 ;
; .
. . Значит
. Значит 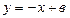 . Параметр
. Параметр  найдем из условия принадлежности точки
найдем из условия принадлежности точки  искомой прямой. Подставляя координаты точки
искомой прямой. Подставляя координаты точки  ,
,  .
. .
. и нормальным вектором
и нормальным вектором  , воспользуемся уравнением (4.2):
, воспользуемся уравнением (4.2): ;
; .
. ,
, 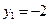 ;
;  ,
,  , получим
, получим  ;
;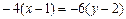 ;
; или
или  .
. :
: ;
; . Прямая проходит через точку
. Прямая проходит через точку  ,
,  . Уравнение искомой прямой приобретает вид:
. Уравнение искомой прямой приобретает вид:  . Осталось найти
. Осталось найти 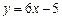 , то
, то  , так как угловые коэффициенты параллельных прямых равны (1.8). Значит
, так как угловые коэффициенты параллельных прямых равны (1.8). Значит  или
или  .
. , то
, то  по условию (4.9). Значит
по условию (4.9). Значит  или
или 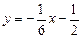 .
. и
и  до биссектрисы первого координатного угла.
до биссектрисы первого координатного угла. пересечения данных прямых. Для этого решим систему по формулам Крамера:
пересечения данных прямых. Для этого решим систему по формулам Крамера:
 ;
;  ;
; 
 ;
;  , т.е.
, т.е.  .
. до прямой
до прямой  или
или  - биссектрисы первого координатного угла:
- биссектрисы первого координатного угла: .
. ,
,  ,
,  . Составить уравнения:
. Составить уравнения: ;
; ;
; на сторону
на сторону  ,
,  ;
;  ,
,  :
:  ;
;  ;
; .
. , найдем координаты точки
, найдем координаты точки 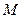 - середины отрезка
- середины отрезка  :
: ,
,  ,
, .
. ,
,  ;
;  ,
, 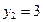 , имеем
, имеем ;
;  ;
; .
. из вершины
из вершины  является нормальным вектором высоты. Воспользуемся уравнением (1.2):
является нормальным вектором высоты. Воспользуемся уравнением (1.2):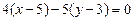 ;
;  .
. ;
;  .
. равен
равен 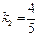 :
:  ;
;  .
. .
. .
.




 , получим
, получим  ,
,  , получим
, получим  .
.
 ,
,  - это точки пересечения прямой с осями координат. Построим прямую (рис. 4.3).
Для определения искомой полуплоскости рекомендуется задать произвольную контрольную точку, не лежащую на ее границе – построенной прямой.
- это точки пересечения прямой с осями координат. Построим прямую (рис. 4.3).
Для определения искомой полуплоскости рекомендуется задать произвольную контрольную точку, не лежащую на ее границе – построенной прямой.
 , не лежащей на построенной прямой. Координаты точки
, не лежащей на построенной прямой. Координаты точки  не удовлетворяют неравенству
не удовлетворяют неравенству  , следовательно, решением данного неравенства является верхняя полуплоскость, не содержащая контрольную точку
, следовательно, решением данного неравенства является верхняя полуплоскость, не содержащая контрольную точку  и образующей с осью
и образующей с осью  .
. ?
?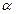 прямая
прямая 
 , зная, что прямая проходит через точки
, зная, что прямая проходит через точки  и
и  .
. и
и  . Какую абсциссу имеет точка
. Какую абсциссу имеет точка  и пересекающей ось
и пересекающей ось  в точке (0; -6);
в точке (0; -6); и отсекающей на оси
и отсекающей на оси 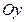 отрезок, равный 2;
отрезок, равный 2;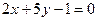 . Составить уравнение прямой, проходящей через точку
. Составить уравнение прямой, проходящей через точку  :
: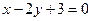 и
и 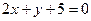 и параллельную оси ординат.
и параллельную оси ординат. в точке пересечения ее с прямой
в точке пересечения ее с прямой  .
. и
и 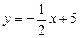 ;
; и
и  ;
; и
и  .
. до прямой
до прямой  .
. и
и  параллельны. Найти расстояние между ними.
параллельны. Найти расстояние между ними. в треугольнике с вершинами
в треугольнике с вершинами  ,
,  и
и  .
.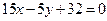

 ;
;  б)
б) 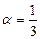
 ;
; 
 ; б)
; б)  ; в)
; в) 
 ; б)
; б) 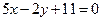


 ; б)
; б)  ; в)
; в) 
