 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Электролитическая диссоциация
Анализ молекулярно-ионных систем с частичной или произвольной степенью (долей) диссоциации α производится на основе ТЗДМ для реакции диссоциации Стехиометрическое произведение концентраций для неидеальных систем должно быть выражено через льюисовские активности компонентов. ТЗДМ для реакции диссоциации называют уравнением диссоциации (ионизации) электролита:
Подставляя равновесные концентрации, выраженные через степень диссоциации α,получим
Для 1,1-валентных электролитов (ν+ = ν− = 1, ν = 2)
Решение квадратного уравнения (4.8''), определяющее степень диссоциации
во взаимосвязи с константой диссоциации Km называют законом разведения Оствальда Простейший анализ решения показывает: 1. Чем больше константа диссоциации, тем больше степень диссоциации. 2. Даже для слабых электролитов (с малой Km < 1) можно повысить степень их диссоциации путем разбавления (m0 → 0). Для очень слабых электролитов, диссоциирующих с образованием того же иона как у растворителя, полной диссоциации электролита не происходит. Такие системы следует анализировать с позиции молекулярных моделей растворов. 4.5. Ионные реакции и равновесия в растворах рассматриваются на основе: 1. Применения термодинамического закона действующих масс (ТЗДМ) к реакциям диссоциации электролитов. 2. Термодинамических функций (химического потенциала) ионных образований в растворах, определяемых теорией Дебая-Хюккеля. Рассмотрение ионных равновесий будет ограничено, во-первых, водными растворами, во-вторых, - сравнительно низкими концентрациями растворенных веществ. Ограничение разбавленными растворами носит более принципиальный характер и обусловлено отсутствием теорий многокомпонентных концентрированных растворов электролитов, в полной мере учитывающих взаимодействие ионов. Электропроводность раствора – простейший способ установить наличие ионов. Уксусная кислота представляет собой типично слабую кислоту, которая при её концентрации ~ 0.1 М диссоциирует в водных растворах всего на 1%. Малая концентрация ионов в растворе характерна и для плохо растворимых солей (AgCl, PbCrO4, CdS и др.). В соответствии с предельным законом Дебая, коэффициенты активности (f± при работе в концентрационной шкале молярностей вместо γ± в шкале моляльностей)будут близки к 1 и активности можно заменить на концентрации компонентов, которые далее в шкале молярностей мы будем обозначать используя квадратные скобки [H3O+]. Химическое уравнение диссоциации уксусной кислоты и соответствующий ТЗДМ в концентрационной форме (индекс С) имеет вид: СH3(CO)OH + H2O = H3O+ + СH3(CO)O−. Для разбавленных растворов [H2O] ≈ 55,5 моль/л – практически постоянная величина, которую можно включить в константу KС . Ион гидроксония H3O+ по-сути является упрощенным отражением гидратной оболочки протона. Его реальную гидратную оболочку принято отмечать индексом "aq": СH3(CO)OHaq = Н+aq + СH3(CO)O−aq . Поскольку в данной теме мы рассматриваем только ионные реакции, то далее индекс "aq"опускаем: СH3(CO)OH = Н++ СH3(CO)O- Константа равновесия ионизации в приложении к кислоте называетсяконстантой ионизации кислоты("acid"). С принципиальной точки зрения константа Kaможет быть вычислена по термодинамическим данным (Δ f HºиΔ f Sº, входящим в μо). Экспериментальное определение Ka основано на измерении электропроводности раствора. Подобные измерения (с ними мы познакомимся при изучении электрохимии) показывают, что 0,1 М раствор уксусной кислоты ионизирован всего на 1,33%. При этом Для раствора слабого основания аммиака NH3 + H2O = NH4+ + OH− соответствующая константа ионизации основания (base), в которую также включена постоянная концентрация воды По случайности Кb аммиака почти точно совпадает с Кa уксусной кислоты 1,8·10-5 . Цианистоводородная кислота ионизована всего на 0,0063%, т.е. в 0,1 М растворе концентрация ионов [H+] = [CN−] =0,1·0,000063 = 6,3 · 10-6 М. Химики условились характеризовать константы ионизации их отрицательным десятичным логарифмом: Кислоты, у которых больше одного ионизированного протона, называются многоосновными. Например, угольная кислота Н2СО3 (растворенный в воде диоксид углерода СО2 или ассоциативный комплекс Н2О·СО2) ионизируется в две стадии: Н2СО3 = Н+ +НСО3− Kа1 = 4,4 · 10-7 НСО3− = Н+ + СО32− Kа2 = 5,6 · 10-11 Угольная кислота используется при выпечке хлеба с использованием пищевой соды – NaHCO3 или ее смесями с порошкообразной кислотой или кислой солью ("сухие дрожжи"). 1) 2NaHCO3 2) NaHCO3 + H+ = Na+ + H2CO3 (CO2↑ + H2O) В результате действия тепла или реакции NaHCO3 с кислотой выделяется CO2, пузырьки которого "поднимают" тесто. Формально для угольной кислоты Ka1·Ka2 = ([H+][HCO3−] / [H2CO3])· ([H+][CO32−]/[HCO3−]) = [H+][CO32−]/[H2CO3] = Ka12 = =2,46·10-17 Последнее равенство соответствует реакции диссоциации H2CO3 = 2 H+ + CO3 2−. Такая форма диссоциации игнорирует наличие основного аниона HCO3-, а потому лишена реального смысла. Тем более это относится к трехосновной ортофосфорной кислоте H3PO4: Ka123=[H+]3[PO43-]/[H3PO4]= 7,9∙10-22 , игнорирующей ионы H2PO4−, HPO42− в количествах, заметно превышающих PO43−. Несмотря на формальное существование, такие константы используются только для пересчетов при определении Ka1, Ka2 … Таблица4.1. Константы ионизации некоторых кислот и оснований (в скобках pK).
Пользуясь данными этой таблицы, можно вычислить концентрации ионов по концентрациям исходных кислот и оснований. Электролитическую диссоциацию (см. раздел 4.4) рассмотрим на простом примере С 0 0 H2S = H+ + HS− Ka1 = ξ2 /(С - ξ) Ka1/С = α2 /(1- α) (4.11) С - ξ ξ ξ для случая малых степеней диссоциации α = ξ/С (ξ « С): ξ= Далее точное решение будем искать в виде поправочного сомножителя f к приближенному (индекс «0»). Подстановка α = f α0 в (4.11) даёт:
Относительная погрешность Для заметно диссоциирующей сернистой кислоты H2SO3 при С = 0,01М, f= 0,542 по формуле (4.12) исправляет поначалу бессмысленное значение α0= Расчет концентрации анионов S2− на второй ступени (стадии) диссоциации H2S дает: Ka12 = Ka1·Ka2 = [H+]2 ·[S2−] / [H2S], [S2−] = Ka1·Ka2·[H2S] / [H+]2 = 9·10-8 ·1,2·10-15 · 0,01/(3·10-5)2 = 1,2·10-15 М.
Поиск по сайту: |
 (4.4′)
(4.4′)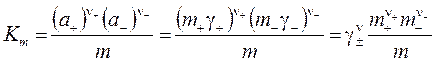 . (4.8)
. (4.8) . (4.8')
. (4.8') (4.8'')
(4.8'') при m0→ 0 и Km → ∞ (4.9)
при m0→ 0 и Km → ∞ (4.9) .
.
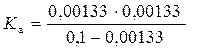 =1,793·10-5 ≈1,8·10-5
=1,793·10-5 ≈1,8·10-5 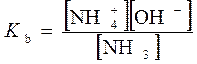 .
.
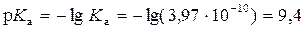
 Na2CO3 + H2CO3 (CO2↑ + H2O)
Na2CO3 + H2CO3 (CO2↑ + H2O) , α0 =
, α0 =  . При С=0,01 моль/л, α0 =
. При С=0,01 моль/л, α0 =  =3∙10-3, ξ0=3∙10-5.
=3∙10-3, ξ0=3∙10-5. (4.12)
(4.12)
 =1,304 до точного значения α = 0,707. Относительная погрешность δ= 84,6 %.
=1,304 до точного значения α = 0,707. Относительная погрешность δ= 84,6 %.