 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Элементарные динамические звенья ⇐ ПредыдущаяСтр 7 из 7
Динамика большинства функциональных элементов САУ независимо от исполнения может быть описана одинаковыми по форме дифференциальными уравнениями не более второго порядка. Такие элементы называют элементарными динамическими звеньями. Передаточная функция элементарного звена в общем виде задается отношением двух полиномов не более чем второй степени: Wэ(p) =
Известно также, что любой полином произвольного порядка можно разложить на простые сомножители не более, чем второго порядка. Так по теореме Виета модно записать D(p) = aopn + a1pn - 1 + a2pn - 2 + ... + an = ao(p - p1)(p - p2)...(p - pn),
где p1, p2, ..., pn - корни полинома D(p). Аналогично
K(p) = bopm + b1pm - 1+ ... + bm = bo(p - p~1)(p - p~2)...(p - p~m),
где p~1, p~2, ..., p~m - корни полинома K(p). То есть
Корни любого полинома могут быть либо вещественными pi = ai, либо комплексными попарно сопряженными pi = ai ± j (p - ai + j
То есть
Поэтому любую сложную передаточную функцию линеаризованной САУ можно представить как произведение передаточных функций элементарных звеньев. Каждому такому звену в реальной САУ, как правило, соответствует какой - то отдельный узел. Зная свойства отдельных звеньев можно судить о динамики САУ в целом. В теории удобно ограничиться рассмотрением типовых звеньев, передаточные функции которых имеют числитель или знаменатель, равный единице, то есть W(p) = Вопросы 1. Какой режим САУ называется динамическим? 2. Что называется регулированием? 3. Назовите возможные виды переходных процессов в САУ. Какие из них являются допустимыми для нормальной работы САУ? 4. Что называется уравнением динамики? Каков его вид? 5. Как провести теоретическое исследование динамики САУ? 6. Что называется линеаризацией? 7. В чем геометрический смысл линеаризации? 8. В чем состоит математическое обоснование линеаризации? 9. Почему уравнение динамики САУ называется уравнением в отклонениях? 10. Справедлив ли для уравнения динамики САУ принцип суперпозиции? Почему? 11. Как звено с двумя и более входами представить схемой, состоящей из звеньев с одним входом? 12. Запишите линеаризованное уравнение динамики в обычной и в операторной формах? 13. В чем смысл и какими свойствами обладает дифференциальный оператор p? 14. Что называется передаточной функцией звена? 15. Запишите линеаризованное уравнение динамики с использованием передаточной функции. Справедлива ли эта запись при ненулевых начальных условиях? Почему? 16. Напишите выражение для передаточной функции звена по известному линеаризованному уравнению динамики: (0.1p + 1)py(t) = 100u(t). 17. Что называется динамическим коэффициентом усиления звена? 18. Что называется характеристическим полиномом звена? 19. Что называется нулями и полюсами передаточной функции? 20. Что называется динамическим звеном? 21. Что называется структурной схемой САУ? 22. Что называется элементарными и типовыми динамическими звеньями? 23. Как сложную передаточную функцию разложить на передаточные функции типовых звеньев?
Поиск по сайту: |
 .
.
 i . Любому вещественному корню при разложении полинома соответствует сомножитель (p - ai). Любая пара комплексно сопряженных корней соответствует полиному второй степени, так как
i . Любому вещественному корню при разложении полинома соответствует сомножитель (p - ai). Любая пара комплексно сопряженных корней соответствует полиному второй степени, так как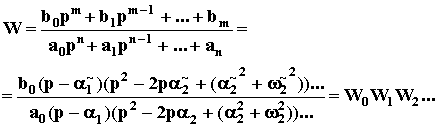
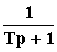 , W(p) =
, W(p) =  , W(p) = 1/p, W(p) = p, W(p) = Tp + 1, W(p) = k. Из них могут быть образованы все остальные звенья. Звенья, у которых порядок полинома числителя больше порядка полинома знаменателя, технически нереализуемы.
, W(p) = 1/p, W(p) = p, W(p) = Tp + 1, W(p) = k. Из них могут быть образованы все остальные звенья. Звенья, у которых порядок полинома числителя больше порядка полинома знаменателя, технически нереализуемы.