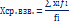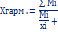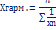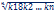|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие средних величин. Основные положения теории средних величин
Средние величины- дают, обобщённую хар-ку изучаемой совокупности, имеется в каждой единице совокупности. Теории средних величин: 1) Индивидуальные значения из которых рассчитывается среднее должны относится к единородной совокупности и их число должно быть значительным. 2) Метод средних должен приниматься вместе с методом группировки. Необходимо предварительное распределение совокупности на однородную группу. 3) необходимость расчёта групповых и общих средних для объективности и полной хар-ке изучаемой совокупности.
Средняя арифметическая простая и взвешенная. Расчёт средней арифметической интервального ряда распределения. Средняя арифметическая простая применяется если каждая значение признака в ряде распределения повторяется 1 или одинаковое число раз.
Средняя арифметическая взвешенная
Расчёт средней арифметической из групповых средних и из относительных величин. Расчёт среднего арифметического из групповых средних применяется формула средней арифметической взвешенной, где xi-групповые средние, за fi-объём каждой группы. Расчёт средней арифметической из относительных величин по арифметической взвешенной, в которой за xi-относительные величины, fi-основание средних величин.
Св-ва средней арифметической. Расчёт способом «моментов». Св-ва: -Если все варианты увеличить или уменьшить на одно число, то средняя величина увеличится или уменьшится на тоже число. -Если все варианты увел. или умен. в несколько раз, то средняя величина умен. или увел. во столько же раз. -Если ве частоты увел. или умен. в несколько раз, то средняя величина не изменится. -Сумма отклонений вариантов от средней арифметической равна нулю. Св-ва величин применяется для упрощения их расчёта.
Средняя гармоническая простая и взвешенная. Если известны произведения xi и fi варианты xi, то для расчёта средней применяется средняя гармоническая. Средняя гармоническая средняя.
Средняя гармоническая простая.
Средняя геометрическая и средняя хронологическая. Применяется для определения средних темпов роста в единицу времени.
Средняя хронологическая. Применяется, если исходные показатели представлены на определение даты, момента времени.
Поиск по сайту: |