 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Связи и реакции связейСтр 1 из 2Следующая ⇒
Аксиомы статики Система сил, приложенная к телу или материальной точке, называется уравновешенной или эквивалентной нулю, если тело под действием этой системы находится в состоянии покоя или движения по инерции. Не нарушая механического состояния тела, к нему можно приложить или отбросить уравновешенную систему сил. О действии и противодействии. При всяком действии одного тела на другое со стороны другого тела имеется противодействие, такое же по величине, но противоположное по направлению. О двух силах. Две силы, приложенные к одному и тому же телу, взаимно уравновешены (их действие эквивалентно нулю) тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны. О равнодействующей. Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и равна диагонали параллелограмма, построенного на этих силах как сторонах. Аксиома затвердевания. Если деформируемое тело находилось в равновесии, то оно будет находиться в равновесии и после его затвердевания. Аксиома о связях. Механическое состояние системы не изменится, если освободить её от связей и приложить к точкам системы силы, равные действовавшим на них силам реакций связей.
Связи и реакции связей
Все законы и теоремы статики справедливы для свободного твердого тела.
Шарнирная опора. Подвижный шарнир. Неподвижный шарнир.
Равнодействующая системы сходящихся сил Силы называются сходящимися, если линии действия всех сил, составляющих систему, пересекаются в одной точке.Теорема: Система сходящихся сил эквивалентна одной силе (равнодействующей), которая равна сумме всех этих сил и проходит через точку пересечения их линий действия. Пусть задана система сходящихся сил F1, F2, F3, ..., Fn, приложенных к абсолютно твердому телу (рис. 2.1, а). Перенесем точки приложения сил по линиям их действия в точку пересечения этих линий (21, б). Получили сист сил, прил к одной точке. Она эквивалентна заданной. Сложим F1 и F2, получим их равнодействующую: R2=F1+F2. Сложим R2 с F3: R3=R2+F3=F1+F2+F3. Сложим F1+F2+F3+…+Fn=Rn=R=åFi. Ч.т.д. Вместо параллелограммов можно построить силовой многоугольник. Пусть система состоит из 4 сил (рис 2.2.). От конца вектора F1 отложим вектор F2. Вектор, соединяющий начало О и конец вектора F2, будет вектором R2. Далее отложим вектор F3 помещая его начало в конце вектора F2. Тогда мы получим вектор R8, идущий от точки О к концу вектора F3. Точно так же добавим вектор F4; при этом получим, что вектор, идущий от начала первого вектора F1 к концу вектора F4, является равнодействующей R. Такой пространственный многоугольник называется силовым. Если конец последней силы не совпадает с началом первой силы, то силовой многоугольник наз разомкнутый. Если для нах равнодействующей исп прав геометр, то этот способ наз геометрическим.
Больше пользуются аналитическим способом для определения равнодействующей. Проекция суммы векторов на некоторую ось равна сумме проекций на ту же ось слагаемых векторов, получим Rx=åFkx=F1x+F2x+…+Fnx; Ry=åFky=F1y+F2y+…+Fny; Rz=åFkz=F1z+F2z+…+Fnz; где Fkx, Fky, Fkz– проекции силы Fkна оси, а Rx, Ry, Rz– проекции равнодействующей на те же оси. Проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на соответствующие оси. Модуль равнодействующей R равен: R=(Rx2+Ry2+Rz2)1/2. Направляющие косинусы равны: cos(x,R)=Rx/R, cos(y,R)=Ry/R, cos(z,R)=Rz/R. Если силы распол в пл-ти то всё аналогично, отсутствует ось Z. Теорема о трех силах
Если под действием трех сил твердое тело находится в равновесии и линии действия двух сил пересекаются в одной точке, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке. Пусть на твердое тело действует система трех сил F1, F2 и F3, причем линии действия первых двух пересекаются в точкеA (рис. 11, a). Согласно следствию из второй аксиомы, силы F1, F2 переносим в точку A(рис. 11, b). Следуя третьей аксиоме, Тело находится в равновесии. Поэтому, по первой аксиоме силы R и F3 должны иметь общую линию действия. Это может быть только тогда, когда исходные три силы лежат в одной плоскости, а линии действия сил пересекаются в одной точке. Теорема доказана. Теорема о трех силах позволяет в ряде задач найти линию действия неизвестной силы, приложенной к твердому телу
условия и уравнения системы сходящихся сил
(F1, F2, ... ,Fn)~R => для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы их равнодействующая равнялась нулю: R = 0. Следовательно, в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой силы; в этом случае говорят, что силовой многоугольник замкнут. Это условие используется при графическом решении задач для плоских систем сил. Векторное равенство R=0 эквивалентно трем скалярным равенствам: Rx=åFkx=F1x+F2x+…+Fnx=0; Ry=åFky=F1y+F2y+…+Fny=0; Rz=åFkz=F1z+F2z+…+Fnz=0; где Fkx, Fky, Fkz– проекции силы Fk на оси, а Rx, Ry, Rz– проекции равнодействующей на те же оси. Т. е. для равновесия сходящейся системы сил необходимо и достаточно равенства нулю алгебраических сумм проекций всех сил данной системы на каждую из координатных осей. Для плоской системы сил пропадает условие, связанное с осью Z. Условия равновесия позволяют проконтролировать, находится ли в равновесии заданная система сил.
Поиск по сайту: |
 Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.
Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.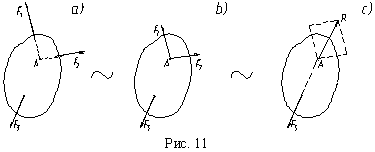 сложим их, заменив их одной силой, равной R=F1+F2. Таким образом, исходная система сил приведена к двум силам R и F3(рис. 11, c).
сложим их, заменив их одной силой, равной R=F1+F2. Таким образом, исходная система сил приведена к двум силам R и F3(рис. 11, c).