 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Частные случаи приведения плоской системы сил
В зависимости от значений главного вектора R0 и главного момента M0 возможны следующие случаи приведения плоской системы сил. 1) R0 =0, M0 =0 - система сил находится в равновесии; 2) R0 =0, M0 ≠0 - система эквивалентна паре сил с моментом, равным главному моменту системы, который в этом случае не зависит от выбора центра приведения; 3) R0 ≠0, M0 =0 - система эквивалентна равнодействующей R, равной и эквивалентной главному вектору системы R0 , линия действия которой проходит через центр приведения: R = R0 , R~R0 ; 4) R0 ≠ 0, M0 ≠0 - система эквивалентна равнодействующей R, равной главному вектору системы R0, ее линия действия проходит на расстоянии d = |M0|/ R0 от центра приведения (рис.20, б). Условия равновесия произвольной плоской системы сил. Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M0 = 0. Здесь О - любая точка плоскости. Из этого условия следуют уравнения равновесия произвольной плоской системы сил, которые можно записать в трех различных формах: 1) Первая форма: ΣMA = 0; ΣX = 0; ΣY = 0. 2) Вторая форма: ΣMA = 0; ΣMB = 0; ΣY = 0, где ось Oy неперпендикулярна отрезку АВ. 3) Третья форма: ΣMA = 0; ΣMB = 0; ΣMС = 0, где точки А, В и С не лежат на одной прямой. Равенства выражают, следующие аналитические условия равновесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю. Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.
Равновесие плоской системы параллельных сил. В случае, когда все действующие на тело силы параллельны друг другу, мы можем направить ось Ох перпендикулярно к силам, а ось Оу параллельно им (рис. 21). Тогда проекция каждой из сил на Ox будет равна нулю и первое из 3-х равенств обратится в тождество вида 0 = 0. В результате для параллельных сил останется два условия равновесия: Где ось Оу параллельна силам.
Рис.21 Сложение параллельных сил. Центр параллельных сил. Пусть даны две параллельные силы
Рис.22
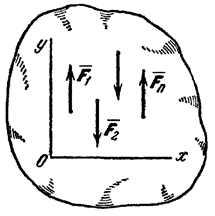
Конечно, величина их равнодействующей Значит Отсюда Если параллельные силы направлены в противоположные стороны (рис.23), то аналогично можно доказать, что равнодействующая по величине будет равна разности сил:
Рис.23
Следует заметить, что если точка приложения равнодействующей расположена на одной прямой с точками A1 и A2, точками приложения сил, то, при повороте этих сил в одну сторону на одинаковый угол, равнодействующая также повернётся вокруг точки приложения С в том же направлении, и останется параллельной им. Такая точка приложения равнодействующей называется центром параллельных сил. Конечно, если хотя бы одну из сил перенести по своей линии действия в другую точку, то и точка приложения равнодействующей, центр параллельных сил, тоже переместится по линии действия. Следовательно, положение центра параллельных сил зависит от координат точек приложения сил. Центром нескольких параллельных сил, найденный последовательным сложением каждых двух сил, будем называть точку С, радиус-вектор которой определяется формулой
Используя (1), нетрудно найти координаты центра параллельных сил. Если радиусы-векторы откладывать из начала координат, то проекции радиусов-векторов точек на оси будут равны их координатам. Поэтому, проектируя векторное равенство (1) на оси, получим
где
Поиск по сайту: |
 .
.
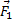 и
и  , направленные в одну сторону и приложенные к точкам
, направленные в одну сторону и приложенные к точкам  и
и  (рис.22).
(рис.22).
 . Вектор её параллелен силам и направлен в ту же сторону. С помощью теоремы Вариньона найдём точку приложения равнодействующей – точку С. По этой теореме
. Вектор её параллелен силам и направлен в ту же сторону. С помощью теоремы Вариньона найдём точку приложения равнодействующей – точку С. По этой теореме  .
.
 . То есть точка приложения равнодействующей делит расстояние между точками A1 и A2 на части обратно пропорциональные силам.
. То есть точка приложения равнодействующей делит расстояние между точками A1 и A2 на части обратно пропорциональные силам.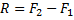 (если
(если  ), параллельна им, направлена в сторону большей силы и расположена за большей силой – в точке С. А расстояния от точки С до точек приложения сил обратно пропорциональны силам:
), параллельна им, направлена в сторону большей силы и расположена за большей силой – в точке С. А расстояния от точки С до точек приложения сил обратно пропорциональны силам: 
 , (1)
, (1)
 - радиусы-векторы точек приложения сил;
- радиусы-векторы точек приложения сил;  – величина равнодействующей параллельных сил, равная алгебраической сумме этих сил (знак силы определяется направлением, которое заранее выбирается и считается положительным).
– величина равнодействующей параллельных сил, равная алгебраической сумме этих сил (знак силы определяется направлением, которое заранее выбирается и считается положительным).
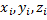 – координаты точек приложения сил.
– координаты точек приложения сил.