 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Табличное и графическое представление статистических данныхСтр 1 из 4Следующая ⇒
Результаты сводки и группировки излагаются в виде таблиц. Таблица – рациональная, наглядная и компактная форма стат.материала. Статистическая таблица – таблица, содержащая результаты подсчета практических данных и является итогом сводки первоначальной информации. Таблица характеризует совокупность по одному или нескольким признакам, взаимосвязанным логикой. Статистическая таблица имеет свое подлежащее и сказуемое. Подлежащее – объект, характеризующийся цифрами. Сказуемое таблицы - система показателей. Таблицы бывают простые и сложные. В простой таблице дается простой перечень объектов. Сложная таблица содержит группировку единиц совокупности одновременно по 2-м и более признакам. Таблица д/б компактной, заголовки краткими, информация в столбцах и графах должна завершаться итоговой строкой. Графы и строки должны иметь единицы измерения, затем необходимо провести четную и логическую проверку таблицы. Статистический график – чертеж, на котором стат.совокупности, характеризуемые определенными показателями описываются с помощью условных геометрических образов или знаков. При построении графика необходимо соблюдать требования: наглядность, выразительность, понятность. Поле графика – часть плоскости, где расположены графические образы. Виды графиков: линейные, столбиковые, полосовые, круговые, секторные, фигурные, точечные, объемные, применяются диаграммы и стат.карты. Картограмма – схематическая географическая карта, на которой выделены отрасли промышленности или структура состава населения.
8. Выражение статистических показателей в виде абсолютных и относительных величин. Их измерители. Основные виды относительных величин. Абсолютные и относительные величины являются обобщающими показателями характеризующими количественную сторону общественных явлений. Абсолютные- именованные числа имеющие определённую размерность и единицы измерения, они характеризуют показатели на момент времени или за период в зависимости от различныз причин и целей анализа применяются натуральные, условно натуральные денежные и трудовые единицы измерения. Относительные – характеризуют количественные соотношения, сравниваемых абсолютных величин. Индивидуальные – характеризуют отдельный объект или единицу совокупности (например, предприятие). Суммарные - характеризуют сумму количества единиц изучаемой совокупности (численность совокупности) или сумму значений варьирующего признака всех единиц совокупности (объем варьирующего признака). В зависимости от сущности исследуемого явления абсолютные величины выражаются в натуральных (тонны, штуки, метры, литры), стоимостных (рубли, доллары) и трудовых (затраты труда, трудоемкость) единицах измерения. Относительная величина – это частное от деления одного абсолютного показателя на другой и дает числовую меру соотношения между ними. Он отражает во сколько раз, сравниваемый абсолютный показатель больше или меньше базисного. Выражается в коэффициентах (%). Виды относительных показателей: относительный показатель динамики (текущий показатель/базисный показатель), планового задания, выполнения плана (факт/план), структуры, сравнения, уровня экономического развития. 9. Средняя величина в статистике, ее сущность и условия применения. Виды и формы средних. Средние величины – в статистике это средний показатель, характерный типичный уровень являющийся в конкретных условиях места и времени, отражающий величину вальирующего признака в расчёте на единицу качественно-однородной совокупности. Среднее отражает характерный типичный реальный уровень изучаемых явлений характеризует эти уровни и их изменения во времени и пространстве. В статистике применяются различные виды средних арифметическое, гармоническое, квадратическое, геометрическое и структурные средние мода и медиана. При расчете средней необходимо соблюдать следующие условия: 1) расчет надо вести только однородных по качеству совокупностей, для этого надо сочетать метод средних и метод группировок; 2) общее среднее необходимо дополнять групповыми средними и индивидуальными величинами; 3) для расчета средней нужна масса единиц (20-30); 4) необходимо правильно выбирать единицу совокупности средних. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д. Средняя арифметическаяприменяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Чтобы рассчитать среднюю арифметическую, нужно сумму всех значений признаков разделить на их число ( Если частоты неравны, то применяется формула средней ариф.взвешанной ( Средняя гармоническая применяется, когда частоты неизвестны, а известны варианты и производные показатели ( Средняя квадратическая: Для изучения внутреннего строения и структуры рядов распределения значений признака применяют структурные средние: Мода– значение признака наиболее часто встречающегося в изучаемой совокупности. Медиана– вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части. 10. Понятие о вариации признака в совокупности. Система показателей вариации. Ее применение в анализе финансово-экономической деятельности предприятия. Вариация– это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов, которые по разному сочетаются в каждом отдельном случае. 1. Дисперсия – средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической (простая 2. Среднее квадратическое отклонение (СКО): СКО показывает на сколько в среднем отклоняются конкретные варианты от их среднего значения. 3. Коэффициент вариации используется для сравнения размеров вариации различных признаков, а также для сравнения степени вариации одноименных признаков в нескольких совокупностях: По этой величине можно судить об однородности состава совокупности. Чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней.
11. Виды дисперсий. Правило сложения дисперсий. Расчет на его основе коэффициента детерминации и эмпирического корреляционного отношения. Их практическое использование. Дисперсия (σ2)- это среднее арифметическое квадратов отклонений отдельных значений признака от икс среднего арифметического, в зависимости от исходных данных σ2 вычисляется по формуле средней арифметической простой или возвешенной простая дисперсия Среднее квадратическое отклонение (σ) – корень квадратный из дисперсии σ=корень из σ2. Для сравнения размеров вариации различных признаков и для сравнения степени вариации одноимённых признаков в нескольких совокупностях исчисляется относительный показатель вариации – коэффициент вариации (V), который представляет собой процентное отношение среднего квадратического отклонения средней арифметической V=σ/икс среднее. По величине коэффициента вариации можно судить о степени вариации признака, а следовательно об однородности состава совокупности, чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу. Для статистической совокупности по изучаемому признаку возможно исчисление трёх видов дисперсии σ2об – общая, частных внутригрупповых – σ2i , и межгрупповой – δ2 . Общая дисперсия характеризует вариацию всех единиц совокупности от общей средней
Межгрупповая дисперсия – отражает вариацию изучаемого признака, которая возникает под влиянием признака фактора, положенного в основу группировки. Она характеризует колеблемость групповых, средних
Средняя внутригрупповых дисперсия – характеризут случайную вариацию каждой отдельной группе, эта вариация возникает под влиянием других неучитываемых факторов и не зависит от условия, положенного в осонову группировки
Общая дисперсия = сумме величин межгрупповых дисперсий и средней из внутригрупповых дисперсий
Если основания группировки являются факторным признаком, то с помощью правил сложения дисперсий, можно измерить силу его влияния на результативный признак, вычислить коэффициент детерминации империческое корреляционное отношение:
Империческое корреляционное отношение:
По абсолютной величине имперического корреляционного отношения может измеряться от 0 до 1. Если η=0, группировочный признак не оказывает влияние на результативный, если η=1, изменение результативного признака полностью обусловлено группировочным признаком, т. е. м/у ними функциональная связь.
12. Метод выборочного наблюдения, его сущность и преимущество. Виды выборки. Определение необходимой численности выборки. Особенности малых выборок. Целью выборочного наблюдения является – определение характеристик генеральной совокупности – генеральной средней, и генеральной доли. Характеристики выборочной совокупности – выборочная средняя, и выборочная доля, отличаются от генеральных характеристик на величину ошибки выборки, по-этому для определения характеристик генеральной совокупности необходимо вычислить ошибку выборки или оштбку репрезентативности, которая определяется для каждого вида выборки и способа отбора. Собственно случайная и механическая выборки: при случайном отборе предельная ошибка выборки для средней и для доли определяется по:
n – численность выборки; m – доля единиц обладающих признакам; t – коэффициент доверия, который определяется по таблице значений, интегральной функции Лапласа при заданной вероятности. При бесповторном случайном и механическом отборе, предельная ошибка выборки определяется по формулам:
Выборочное наблюдение – наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность. Совокупность, из которой производится отбор, называется генеральной. Совокупность отобранных единиц именуют выборочной совокупностью. Основная задача выборочного наблюдения состоит в том, чтобы на основе характеристик выборочной совокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности; при групповом отборе – качественно однородные группы или серии изучаемых единиц; комбинированный отбор предполагает сочетание первого и второго видов. По методу выборки различают повторную и бесповторную выборки. При повторной выборке общая численность единиц генеральной совокупности в процессе выборки остается неизменной. При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует. Виды выборки: собственно-случайная, механическая, типическая, серийная, комбинированная. К собственно-случайной выборке относится отбор единиц из всей генеральной совокупности посредством жеребьевки. Механическая выборка - отбор единиц в выборочную совокупность из генеральной производится таким образом, что из каждой группы в выборку отбирается лишь одна единица. Типическая выборка используется, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, влияющим на изучаемые показатели. Серийная выборка предполагает случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (серий) с тем, чтобы в таких группах подвергать наблюдению все без исключения единицы. Комбинированная выборка заключается в объединении различных способов выборки, рассмотренных ранее.
13. Средняя и предельная ошибки выборки. Методика их расчета для средней и доли. Оценка существенности расхождения выборочных средних. Основные характеристики параметров генеральной и выборочной совокупностей обозначаются символами: N – объем генеральной совокупности (число входящих в нее единиц); n – объем выборки (число обследованных единиц); Средняя ошибка выборки при повторном отборе рассчитывается по следующим формулам: для средней количественного признака:
14. Виды и формы взаимосвязей социально-экономических явлений. Корреляционная связь, ее особенности, методы выявления и оценки тесноты. Статистическое изучение связи можно разделить на три этапа: 1. Это качественный анализ, который связан с анализом природы социального или экономического явления. Этот анализ проводится либо методами экономической теории или методами социологии. 2. Это построение модели связи. Базируется на статистических методах. Это способ группировки. 3. Инторпритация полученных результатов. Связан с качественными особенностями изучаемого явления. Между различными явлениями и их признаками необходимо прежде всего выделить два типа связей: функциональную и статистическую. Связь признака y с признаком x называется функциональной связью y=f(x). Эта связь жёсткая детермированная f(xi)= f(xj). X – факторный признак, Y – результативный признак. Чаще всего функциональные связи наблюдаются в явлениях описываемых математикой, физикой и другими точными науками. Имеют место эти связи и в социально-экономических науках. Стохастическая связь – это связь между величинами, при которой одна из них, случайная величина y, реагирует на изменение другой величины x или других величин x1,x2,…,xn, измененм закона распределения. Характерной особенностью стохастических связей является то, что они проявляются во всей совокупности, а не в каждой её единице. Модель стохастической связи может быть представлена в общем виде уравнением: yi=f(xi)+Ei. f(xi) – это часть результативного признака, сформулированного под влиянием нашего факторного признака x. E – часть результативного признака, который возник по действием неучтённых факторов, кроме x. Частным случаем стохастической связи является Корреляционная связь - существует там, где взаимосвязанные явления характеризуются только случайными величинами. При такой связи среднее значение случайной величины результативного признака закономерно изменяется в зависимости от изменения другой величины или других случайных величин. Корреляционная связь проявляется не в каждом отдельном случае, а во всей совокупности в целом. Связи классифицируются: по направлению (прямые – направление изменения результативного признака совпадает с направлением изменения признака-фактора и обратные); по аналитическому выражению (линейные – с возрастанием значений факторного признака происходит непрерывное возрастание значений результативного признака, нелинейные, криволинейные – с возрастанием значения факторного признака возрастание результативного признака происходит неравномерно); по степени тесноты связи, степень тесноты определяется по величине коэффициента корреляции (слабые и тесные).
15. Корреляционно-регрессионный анализ взаимосвязей социально-экономических явлений, его сущность и этапы. Уравнение регрессии как форма аналитического выражения связи. Корреляционный метод анализа решает две задачи: 1. Установление факта наличия связи. 2. Измерение тесноты корреляционной связи по эмпирическим данным. 1. Задача: Есть ряд методов выявления связи: 1. Приведение параллельных рядов данных. 2. Графический. 3. Метод корреляционной таблицы – это специальная комбинационная таблица в которой проведена группировка по двум признакам по факторному и результативному. Концентрация частот около диагонали матрицы свидетельствует о прямой связи, а концентрация частот около побочной диагонали о наличии обратной связи между признаками. 4. Метод аналитической группировки. В статистике различают: парную корреляцию (взаимосвязь между двумя признаками); частная корреляция (когда рассматривается зависимость между результативными признаками и одним из факторных при фиксированном значении всех остальных факторных признаков); множественная корреляция (зависимость между результативным и 2 или более факторных признаков). 2 Задача: Для измерения тесноты связи используется специальный коэффициент, который количественно выражает тесноту связи. Теснота корреляционной связи может быть измерена эмпирическим корреляционным отношением Задачи регрессионного анализа – выбор типа модели, установление степени влияния независимых переменных на зависимую и определение расчётных значений зависимости переменной. Для линейной связи вычисляется линейный коэф. корреляции (показывает направление связи)
16. Методика построения однофакторной регрессионной модели корреляционной связи. Анализ качества модели. Наиболее распространенной в теории статистики является методология так называемой парной корреляции, рассматривающая влияние вариации факторного признака х на результативный у и представляющая собой однофакторный корреляционный и регрессионный анализ. Важнейшим этапом построения модели является установление в анализе исходной информации математической функции.. В основу выявления и установления аналитической формы связи положено применение в анализе исходной информации математических функций. Так при анализе прямолинейной зависимости применяется уравнение однофакторной (парной) линейной корреляционной связи При изучении корреляционной связи показателей анализу подвергаются сравнительно небольшие по составу единиц совокупности. При численности объектов анализа до 30 единиц возникает необходимость испытания параметров уравнения регрессии на их типичность. При этом осуществляется проверка, насколько вычисленные параметры характерны для отображаемого комплекса условий. Применительно к совокупностям, у которых п < 30, для проверки типичности параметров уравнения регрессии используется t-критерий Стьюдента. При этом вычисляют расчетные (фактические) значения t-критерия: для параметра а0
17. Ряды динамики, их виды и особенности, графическое изображение. Правила построения динамических рядов. Сопоставимость уровней рядов динамики. Смыкание уровней динамических рядов, приведение динамических рядов к единому основанию. При изучении в рядах динамики основной тенденцией развития является различные приёмы и методы. Метод укрепления – интервалов основан на укрупнении периодов времени к которым относятся уровни ряда; Метод скользящей средней – замена абсолютных данных средними арифметическими за определённые периоды, расчёт средних ведётся способом скольжения, т. е. постепенным исключением из принятого уровня и включением. Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, т.е. их динамика. Эта задачи решается при помощи анализа рядов динамики (временных рядов). Ряд динамики (динамический ряд) представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени. В каждом ряду динамики имеются два основных элемента: время t и конкретное значение показателя (уровень ряда) у. Уровни ряда– это показатели, числовые значения которых составляют динамический ряд. Время t – это моменты или периоды, к которым относятся уровни. Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития общественных явлений во времени. Эти закономерности не проявляются четко на каждом конкретном уровне, а лишь в тенденции, в достаточно длительной динамике. На основную закономерность динамики накладываются другие, прежде всего случайные, иногда сезонные влияния. Выявление основной тенденции в изменении уровней, именуемой трендом, является одной из главных задач анализа рядов динамики. По времени, отраженному в динамических рядах, они разделяются на моментные и интервальные. Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенные даты (моменты времени). Поскольку в каждом последующем уровне содержится полностью или частично значения предыдущего уровня, суммировать уровни моментного ряда не следует, т.к. это приводит к повторному счету. Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явлений за конкретный период времени (год, квартал, месяц). Значения уровней интервального ряда не содержатся в предыдущих или последующих показателях, их можно просуммировать, что позволяет получать ряды динамики более укрупненных периодов. Интервальный ряд, где последовательные уровни могут суммироваться, можно представить как ряд с нарастающими итогами. При построении таких рядов производится последовательное суммирование смежных уровней. Этим достигается суммарное обобщение результата развития изучаемого явления с начала отчетного периода. Уровни в динамическом ряду могут быть представлены абсолютными, средними или относительными величинами. По расстоянию между уровнями ряды динамики подразделяются на ряды с равностоящими и неравностоящими уровнями по времени. Ряды динамики могут быть изображены графически. Графическое изображение позволяет наглядно представить развитие явления во времени и способствует проведению анализа уровней. Наиболее распространенным видом графического изображения для аналитических целей является линейная диаграмма, которая строится в прямоугольной системе координат: на оси абсцисс отмечается время, а на оси ординат – уровни ряда. Наряду с линейной диаграммой для графического изображения рядов динамики в целях популяризации широко используются столбиковая диаграмма, секторная диаграмма и т.д. Правила построения рядов динамики: 1. полнота показателей ряда динамики; 2. точность, достоверность показателей ряда динамики; 3. периодизация; 4. сопоставимость показателей ряда динамики по методологии и построению; 5.сопоставимость показателей ряда динамики по территории; 6. сопоставимость показателей ряда динамики во времени; 7. сопоставимость показателей ряда динамики по одинаковому кругу охватываемых объектов; 8. совокупность показателей единицы измерения.
18. Аналитические показатели ряда динамики: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста. Средние показатели в рядах динамики. Коэффициенты опережения (отставания) рядов динамики. Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней. К таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента. Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, - базисным. Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и ем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динами, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными. Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными.Важнейшим статистическим показателем анализа динамики является абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста. Абсолютный прирост:цепной прироста за этот период времени, %:
19. Методы выявления основной тенденции развития уровней рядов динамики. Прогнозирование уровней динамических рядов в финансово-экономическом анализе. Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие других факторов может быть кратковременным или носить случайный характер. Поэтому при анализе динами речь идет об основной тенденции, достаточно стабильной (устойчивой) на протяжении изученного этапа развития. Основной тенденцией развития (ТРЕНДОМ) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний. Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания. Наиболее простым методом изучения основной тенденции в рядах динамики является укрупнение интервалов. Данный метод основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Главное в этом методе заключается в преобразовании первоначального ряда динамики в ряды более продолжительных периодов (месячные в квартальные, квартальные в годовые и т.д.). Выявление основной тенденции может осуществляться также методом скользящей (подвижной) средней. Сущность его заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3, 5, 7 и т.д.), первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная со среднего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок. Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следовательно, происходит потеря информации. Для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики. Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:
Поиск по сайту: |
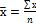 ), х – значения признака, n – число вариант.
), х – значения признака, n – число вариант. ), х – значения признака, f - веса средней или частота.
), х – значения признака, f - веса средней или частота.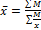 ), х – значения признака, М-веса средней.
), х – значения признака, М-веса средней. .
. , взвешенная
, взвешенная  , межгрупповая). Для характеристики качества статистических оценок используется их дисперсия.
, межгрупповая). Для характеристики качества статистических оценок используется их дисперсия.
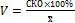
 или взвешенная дисперсия
или взвешенная дисперсия  .
.
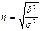 .
.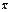 - генеральная средняя (среднее значение признака в генеральной совокупности);
- генеральная средняя (среднее значение признака в генеральной совокупности);  - выборочная средняя; p– генеральная доля (доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности); w – выборочная доля. Доля выборки есть отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:
- выборочная средняя; p– генеральная доля (доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности); w – выборочная доля. Доля выборки есть отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:  . Применяя выборочный метод в статистике, обычно используют два основных вида обобщающих показателя: среднюю величину количественного признака и относительную величину альтернативного признака (долю или удельный вес единиц в статистической совокупности, которые отличаются от всех других единиц этой совокупности только наличием изучаемого признака). Выборочная доля ( w ), или частость, определяется отношением числа единиц, обладающих изучаемым признаком т, к общему числу единиц выборочной совокупности п: w = т / п . Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки. Ошибка выборки
. Применяя выборочный метод в статистике, обычно используют два основных вида обобщающих показателя: среднюю величину количественного признака и относительную величину альтернативного признака (долю или удельный вес единиц в статистической совокупности, которые отличаются от всех других единиц этой совокупности только наличием изучаемого признака). Выборочная доля ( w ), или частость, определяется отношением числа единиц, обладающих изучаемым признаком т, к общему числу единиц выборочной совокупности п: w = т / п . Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки. Ошибка выборки  или, иначе говоря, ошибка репрезентативности представляет собой разность соответствующих выборочных и генеральных характеристик: для средней количественного признака
или, иначе говоря, ошибка репрезентативности представляет собой разность соответствующих выборочных и генеральных характеристик: для средней количественного признака  ;для доли (альтернативного признака)
;для доли (альтернативного признака)  . Выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.
. Выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки. ; для доли (альтернативного признака):
; для доли (альтернативного признака):  . Средняя ошибка выборки при бесповторном отборе рассчитывается по следующим формулам: для средней качественного признака
. Средняя ошибка выборки при бесповторном отборе рассчитывается по следующим формулам: для средней качественного признака  ; для доли (альтернативного признака)
; для доли (альтернативного признака)  . В каждой конкретной выборке расхождение между выборочной средней и генеральной
. В каждой конкретной выборке расхождение между выборочной средней и генеральной  может быть меньше средней ошибки
может быть меньше средней ошибки  , равно ей или больше ее. Причем каждое из этих расхождений имеет различную вероятность. Поэтому фактические расхождения между выборочной средней и генеральной можно рассматривать как некую предельную ошибку, связанную со средней ошибкой и гарантируемую с определенной вероятностью Р. Предельную ошибку выборки можно рассчитать по следующим формулам: при повторном отборе: для средней
, равно ей или больше ее. Причем каждое из этих расхождений имеет различную вероятность. Поэтому фактические расхождения между выборочной средней и генеральной можно рассматривать как некую предельную ошибку, связанную со средней ошибкой и гарантируемую с определенной вероятностью Р. Предельную ошибку выборки можно рассчитать по следующим формулам: при повторном отборе: для средней  , где t – нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки;
, где t – нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки;  - средняя ошибка выборки; для доли
- средняя ошибка выборки; для доли 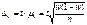 ; при бесповторном отборе:для средней
; при бесповторном отборе:для средней  ; для доли
; для доли  . При вероятности 0,683 коэффициент t = 1; при вероятности 0,954 коэффициент t = 2; при вероятности 0,997 коэффициент t = 3. Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:для средней
. При вероятности 0,683 коэффициент t = 1; при вероятности 0,954 коэффициент t = 2; при вероятности 0,997 коэффициент t = 3. Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:для средней  ;
;  ; для доли
; для доли  ;
;  . Наряду с абсолютным значением предельной ошибки выборки рассчитывается также и предельная относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности: для средней, %:
. Наряду с абсолютным значением предельной ошибки выборки рассчитывается также и предельная относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности: для средней, %:  ; для доли, %:
; для доли, %:  .
. , когда межгрупповая дисперсия
, когда межгрупповая дисперсия  характеризует отклонение групповых средних результативного признака от общей средней:
характеризует отклонение групповых средних результативного признака от общей средней:  .
. ,где r-линейный коэф.корреляции; х-значение факторного признака;
,где r-линейный коэф.корреляции; х-значение факторного признака;  -среднее значение факторного признака; у-знач.результативного призн.;
-среднее значение факторного признака; у-знач.результативного призн.;  -среднее знач.рез.признака ; n-число элементов ряда;
-среднее знач.рез.признака ; n-число элементов ряда;  -средние квадратич.отклонения факторного признака. Коэф.коррел. может изменятся от -1 до +1. Если значение отрицательно, то связь обратная (с возрастанием факторного признака результат.уменьшается) При любой форме связи можно воспользоваться коэф. Фехнера. Он основан на сравнении знаков отклонений отдельных значений признаков от средней.
-средние квадратич.отклонения факторного признака. Коэф.коррел. может изменятся от -1 до +1. Если значение отрицательно, то связь обратная (с возрастанием факторного признака результат.уменьшается) При любой форме связи можно воспользоваться коэф. Фехнера. Он основан на сравнении знаков отклонений отдельных значений признаков от средней.  где С-число совпадений знаков, Н-число несовпадений. Этот коэф. изменяется от +1 до -1, если он равен +1 то имеется согласованная прямая изменчивость; при 0 согласованная изменчивость отсутствует; при -1 имеется обратная согл.изменчивость. Также при любой форме связи можно исчислить теоретическое корреляционное отношение. Данный показатель следует рассчитывать после того, как установлена форма связи и рассчитано уравнение регрессии: у= ах+в
где С-число совпадений знаков, Н-число несовпадений. Этот коэф. изменяется от +1 до -1, если он равен +1 то имеется согласованная прямая изменчивость; при 0 согласованная изменчивость отсутствует; при -1 имеется обратная согл.изменчивость. Также при любой форме связи можно исчислить теоретическое корреляционное отношение. Данный показатель следует рассчитывать после того, как установлена форма связи и рассчитано уравнение регрессии: у= ах+в  , где
, где 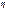 -теоретич.коррел.отношение;
-теоретич.коррел.отношение;  -дисперсия теоретических уровней. Теоретич.коррел.отношение изменяется от 0 до 1, чем ближе к 1 тем теснее связь. Количественную зависимость изменения значения ух от изменения х исчисляется коэф.эластичности. Он характеризует на сколько процентов увеличится ух при увеличении х на один процент:
-дисперсия теоретических уровней. Теоретич.коррел.отношение изменяется от 0 до 1, чем ближе к 1 тем теснее связь. Количественную зависимость изменения значения ух от изменения х исчисляется коэф.эластичности. Он характеризует на сколько процентов увеличится ух при увеличении х на один процент:  Также для всех форм связи можно рассчитать индекс корреляции (измеряет тесноту связи)
Также для всех форм связи можно рассчитать индекс корреляции (измеряет тесноту связи)  Индекс коррел. изменяется от 0до 1, Когда он равен 0, то связи между вариацией признаков у и х нет (когда линия ух .совпадает на чертеже с линией
Индекс коррел. изменяется от 0до 1, Когда он равен 0, то связи между вариацией признаков у и х нет (когда линия ух .совпадает на чертеже с линией  ). Когда индекс кор. равен 1, то связь функциональная,полная. (линия ух сольется на чертеже с линией у. Это означает что изменение у целиком опред. изменением х).
). Когда индекс кор. равен 1, то связь функциональная,полная. (линия ух сольется на чертеже с линией у. Это означает что изменение у целиком опред. изменением х). . Коэффициент парной линейной регрессии а1 имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Уравнение связи показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его измерения, т.е. вариацию у, приходящуюся на единицу вариации х. Знак а1 указывает направление этого изменения. Параметры уравнения а0, а1 находят методом наименьших квадратов. В основу метода положено требование минимальности сумм квадратов отклонений эмпирических данных yi от выравненных
. Коэффициент парной линейной регрессии а1 имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Уравнение связи показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его измерения, т.е. вариацию у, приходящуюся на единицу вариации х. Знак а1 указывает направление этого изменения. Параметры уравнения а0, а1 находят методом наименьших квадратов. В основу метода положено требование минимальности сумм квадратов отклонений эмпирических данных yi от выравненных  : ∑(yi-y)2=∑(yi-a0-a1xi)2--- min. Для нахождения минимума данной функции приравниваем к нулю её частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:
: ∑(yi-y)2=∑(yi-a0-a1xi)2--- min. Для нахождения минимума данной функции приравниваем к нулю её частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:  . Параметры уравнения парной линейной регрессии можно вычислить по следующим формулам:
. Параметры уравнения парной линейной регрессии можно вычислить по следующим формулам:  . Определив значения а0, а1 и подставив их в уравнение связи, получаем значения
. Определив значения а0, а1 и подставив их в уравнение связи, получаем значения  , зависящие только от заданного значения х.
, зависящие только от заданного значения х. ; для параметра а1
; для параметра а1 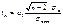 , где п – объем выборки,
, где п – объем выборки,  - среднее квадратическое отклонение результативного признака у от выровненных значений
- среднее квадратическое отклонение результативного признака у от выровненных значений  ;
;  - среднее квадратическое отклонение факторного признака х от общей средней
- среднее квадратическое отклонение факторного признака х от общей средней  . Вычисленные значения сравниваются с критическими t, которые определяются по таблице. Параметр признается значимым (существенным) при условии, если tрасч > tтабл. В зависимости от того какой получится результат наша гипотеза принимается или отвергается.
. Вычисленные значения сравниваются с критическими t, которые определяются по таблице. Параметр признается значимым (существенным) при условии, если tрасч > tтабл. В зависимости от того какой получится результат наша гипотеза принимается или отвергается. ; базисный
; базисный  . Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени
. Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени  . Для оценки интенсивности, т.е. Относительного изменения уровня динамического ряда за какой-либо период времени исчисляют темпы роста (снижения). Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному. Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели интенсивности отличаются только единицами измерения. Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число. Коэффициент роста:цепной
. Для оценки интенсивности, т.е. Относительного изменения уровня динамического ряда за какой-либо период времени исчисляют темпы роста (снижения). Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному. Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели интенсивности отличаются только единицами измерения. Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число. Коэффициент роста:цепной  ; базисный
; базисный  . Темп роста:цепной
. Темп роста:цепной  ; базисный
; базисный  . Таким образом,
. Таким образом,  . Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период
. Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период  , а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпы роста. Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения). Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения. Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах или в долях единицы (коэффициенты прироста). Темп прироста:цепной
, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпы роста. Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения). Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения. Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах или в долях единицы (коэффициенты прироста). Темп прироста:цепной  ; базисный
; базисный  . Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием единицы из коэффициента роста:
. Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием единицы из коэффициента роста:  ;
;  . При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и пророста. Чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу
. При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и пророста. Чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу
 , где
, где  - уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t. Определение теоретических (расчетных) уровней
- уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t. Определение теоретических (расчетных) уровней  производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппоркисимирует) основную тенденцию ряда динамики. Выбор модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики. Простейшими моделями, выражающими тенденцию развития, являются: линейная функция – прямая
производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппоркисимирует) основную тенденцию ряда динамики. Выбор модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики. Простейшими моделями, выражающими тенденцию развития, являются: линейная функция – прямая  , где а0,а1 – параметры уравнения, t – время; показательная функция
, где а0,а1 – параметры уравнения, t – время; показательная функция 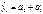 ; степенная функция – кривая второго порядка (парабола)
; степенная функция – кривая второго порядка (парабола)  . Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпирическими уровнями:
. Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпирическими уровнями: 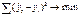 . Выравнивание по прямой применяется в тех случаях, когда абсолютные прироста практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии (или близко к ней). Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны. Выравнивание ряда динамики по прямой:
. Выравнивание по прямой применяется в тех случаях, когда абсолютные прироста практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии (или близко к ней). Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны. Выравнивание ряда динамики по прямой:  . Параметры а0, а1 согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений:
. Параметры а0, а1 согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений:  , где у – фактические (эмпирические) уровни ряда; t – время (порядковый номер периода или момента времени). Расчет параметров значительно упрощается, если за начало отсчета времени (t = 0) принять центральный интервал (момент). Т.о., система принимает вид
, где у – фактические (эмпирические) уровни ряда; t – время (порядковый номер периода или момента времени). Расчет параметров значительно упрощается, если за начало отсчета времени (t = 0) принять центральный интервал (момент). Т.о., система принимает вид  . Таким образом, получаем:
. Таким образом, получаем:  ;
;  .
.