 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие о множественной корреляции⇐ ПредыдущаяСтр 16 из 16
Зависимость между тремя и более признаками называется множественной или многофакторной корреляционной зависимостью. Линейная связь между тремя признаками выражается уравнением:
Теснота связи между тремя признаками измеряется с помощью множественного (совокупного) коэффициента корреляции: Наряду с парными коэффициентами вычисляются и частные коэффициенты корреляции. Они характеризуют тесноту связи между парой признаков при условии элиминирования (закрепления на среднем уровне) значений остальных признаков. Применительно к взаимосвязи трех признаков частные коэффициенты корреляции исчисляются:
Множественный коэффициент корреляции в квадрате (R2) называется коэффициентом детерминации. Он показывает долю вариации результативного признака, обусловленную вариацией факторных признаков, включенную в регрессионную модель. Для многофакторных регрессионных моделей с числом факторов больше двух целесообразно множественный коэффициент корреляции исчислять по формуле:
Множественный коэффициент детерминации вычисляется по формуле: В приведенной формуле каждое из выражений, входящих в сумму значений, показывает долю вариации результативного признака, обусловленную вариацией каждого из факторов регрессионной модели. Адекватность уравнения регрессии оценивается по F- критерию Фишера. Эмпирическое значение критерия Fэмп. Рассчитывается по формуле:
Для оценки уравнений первого порядка (уравнений прямой) используется критерий линейности, исчисляемый по формуле: Составляя разность квадратов корреляционного отношения и коэффициента корреляции с ее основной ошибкой, судят о возможности выбора линейной формы связи между признаками. Если окажется, что отношение
Поиск по сайту: |
 а система нормальных уравнений для определения параметров а0, а1 и а2 будет следующей:
а система нормальных уравнений для определения параметров а0, а1 и а2 будет следующей:
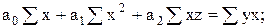

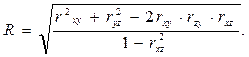 Где
Где  - парные коэффициенты корреляции.
- парные коэффициенты корреляции.
 .
. , где r12, r13, …, r1p – парные коэффициенты корреляции между результативным и каждым из факторных признаков, включенных в регрессионную модель:
, где r12, r13, …, r1p – парные коэффициенты корреляции между результативным и каждым из факторных признаков, включенных в регрессионную модель:  - бетта-коэффициенты – это коэффициенты регрессии в стандартизованном масштабе, показывающие, на какую величину среднеквадратического отклонения (сигмы) изменится результативный признак, если каждый из факторных признаков увеличится на одну сигму. Бетта-коэффициенты рассчитываются:
- бетта-коэффициенты – это коэффициенты регрессии в стандартизованном масштабе, показывающие, на какую величину среднеквадратического отклонения (сигмы) изменится результативный признак, если каждый из факторных признаков увеличится на одну сигму. Бетта-коэффициенты рассчитываются: 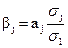 , где aj – коэффициенты регрессии при каждом из признаков – факторов; σ1 - среднеквадратическое отклонение результативного признака; σj - среднеквадратические отклонения по каждому из факторных признаков.
, где aj – коэффициенты регрессии при каждом из признаков – факторов; σ1 - среднеквадратическое отклонение результативного признака; σj - среднеквадратические отклонения по каждому из факторных признаков.
 n- число единиц совокупности; m – число параметров уравнения. Fэмп. сравнивается с заданным уровнем значимости
n- число единиц совокупности; m – число параметров уравнения. Fэмп. сравнивается с заданным уровнем значимости  и числом степеней свободы V1=m-1 и V2=n-m c Fтабл. Если
и числом степеней свободы V1=m-1 и V2=n-m c Fтабл. Если  , то уравнение регрессии признается надежным (значимым).
, то уравнение регрессии признается надежным (значимым). с основной ошибкой
с основной ошибкой  .
. , то, значит, что связь между исследуемыми признаками не может быть представлена уравнением прямой. В подобных случаях отыскиваются другие формы выражения связи.
, то, значит, что связь между исследуемыми признаками не может быть представлена уравнением прямой. В подобных случаях отыскиваются другие формы выражения связи.