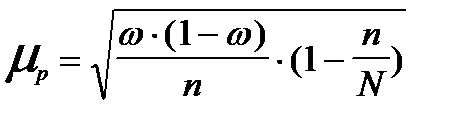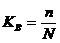|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Способы отбора единиц в выборочную савокупностьСтр 1 из 2Следующая ⇒
Основные характеристики генеральной и выборочной савокупности
Выборка характеризуется следующими показателями: x = t — предельная ошибка выборки, она дает возможность выяснить, в каких пределах находится величина генеральной средней; x = w = tw — предельная ошибка выборочной доли (W); w = Средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности. Однако о величине этой ошибки можно судить с определенной вероятностью. На величину вероятности указывает множитель t. Обычно используются нормированные значения t, для определенных значений вероятности Ф(t):
Зная выборочную среднюю величину признака ( Зная выборочную долю признака (w) и предельную ошибку выборки (
Предельная ошибка рассчитывается по-разному в зависимости от способа отбора при проведении выборки. Для бесповторного способа отбора в формулы средней ошибки выборки вносится поправка: где n - объем выборочной совокупности; N - объем генеральной совокупности Бесповторным называется такой отбор, при котором попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор. Способы отбора единиц в выборочную савокупность. В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения. Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности. Существуют следующие способы отбора единиц из генеральной совокупности: Выборка может быть: § собственно-случайная состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е.
§ механическая состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке — каждая 20-я единица (1:0,05) и т.д. Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица. § типическая –при которойгенеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность; § серийная - при которой генеральную совокупность делят на одинаковые по объему группы - серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию; § комбинированная - выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц. В статистике различают следующие способы отбора единиц в выборочную совокупность: § одноступенчатая выборка - каждая отобранная единица сразу же подвергается изучению по заданному признаку (собственно-случайная и серийная выборки); § многоступенчатая выборка - производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы (типическая выборка с механическим способом отбора единиц в выборочную совокупность). Кроме того различают: § повторный отбор – по схеме возвращенного шара. При этом каждая попавшая в выборку единица иди серия возвращается в генеральную совокупность и поэтому имеет шанс снова попасть в выборку; § бесповторный отбор – по схеме невозвращенного шара. Он имеет более точные результаты при одном и том же объеме выборки.
Поиск по сайту: |

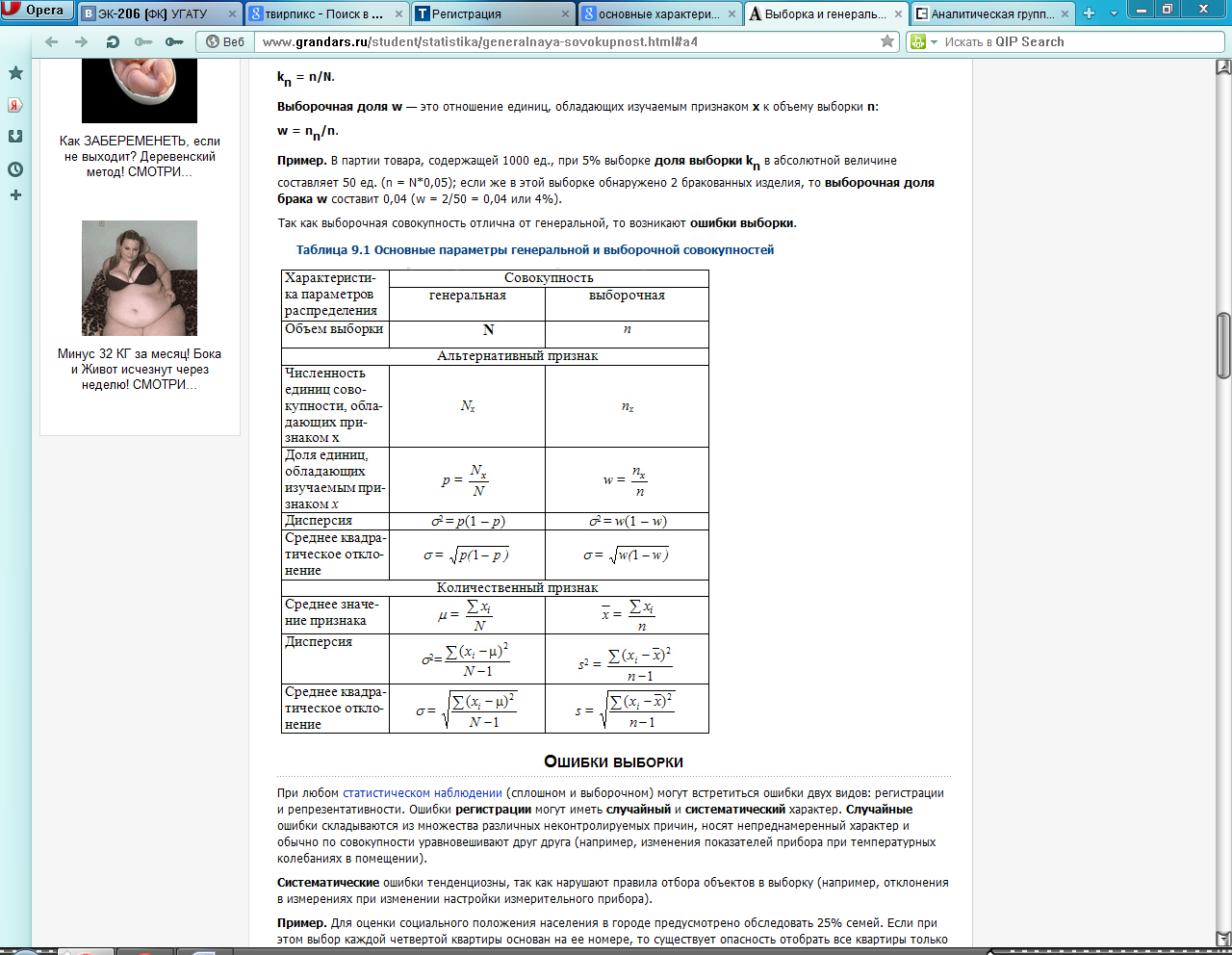
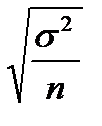 — средняя ошибка выборки, она зависит также и от способа отбора выборки (2 — генеральная дисперсия, n — объем выборочной совокупности).
— средняя ошибка выборки, она зависит также и от способа отбора выборки (2 — генеральная дисперсия, n — объем выборочной совокупности).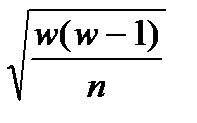 — средняя ошибка выборочной доли.
— средняя ошибка выборочной доли.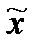 ) и предельную ошибку выборки (Dx), можно определить границы (пределы), в которых заключена генеральная средняя (
) и предельную ошибку выборки (Dx), можно определить границы (пределы), в которых заключена генеральная средняя (  ):
): 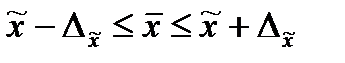 или
или 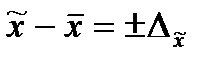
 ), можно определить границы, в которых заключена генеральная доля (р):
), можно определить границы, в которых заключена генеральная доля (р):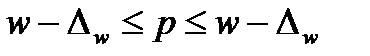
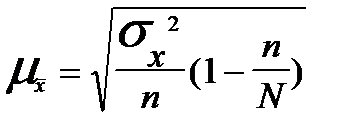 ;
;