 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Связь между неограниченной и бесконечно большой функцией
Из определения ограниченной функции следует, что если 9. Сравнимые и несравнимые бесконечно малые функции
Понятия 10.Функция 12.Пусть 14.Пусть 15.Пусть Умения
Решение: Это бесконечно малые функции.
функции эквивалентны -
Решение: Это бесконечно малые функции.
Так как предел равен конечному числу, отличному от нуля, то функции
Решение: Это бесконечно малые функции.
функция
Решение: Это бесконечно большие функции.
10. Свойства o(f)
Понятия 10.Функция Утверждения Свойства бесконечно малых функций 1°. Сумма конечного числа бесконечно малых функций есть функция бесконечно малая. 2°. Произведение ограниченной функции на бесконечно малую есть бесконечно малая функция. 3°. Произведение функции, имеющей конечный предел, на бесконечно малую есть бесконечно малая функция. 11. Свойства o(f) и O(f)
Понятия 10.Функция 11.Функция Утверждения 20*. Свойства o(f) и O(f) 1°. 2°. 3°. 4°. 5°. 6°. 7°. 8°.
Поиск по сайту: |
, то есть функция является бесконечно большой, то она является неограниченной. Однако обратное неверно: неограниченная функция может не быть бесконечно большой.
называется бесконечно малой в точке 
, если предел этой функции в точке 
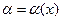и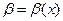 
- две функции, заданные для одних и тех же значений аргумента и обе являющиеся бесконечно малыми в точке 
. Функции 
равен конечному числу, отличному от нуля.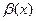
- две функции, заданные для одних и тех же значений аргумента и обе являющиеся бесконечно малыми в точке 
, и обозначается 
.
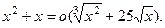
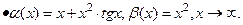
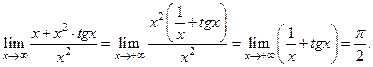
и 
и 
одного порядка роста.
, где 
.
, где 
.
.
.
.
.
.