 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тригонометрическая форма комплексного числаСтр 1 из 2Следующая ⇒
Основные определения Комплексным числом z называется выражение вида z = x + jy, где х, у – действительные числа, j – «мнимая единица», j2 = -1. Числох называется действительной частью комплексного числа z и обозначается x = Re z, ау – мнимой частью z, y = Im z. Если действительная часть комплексного числа равна нулю, х = 0, то такое число называетсячисто мнимым z = jy.Если мнимая часть равна нулю, то число отождествляется с действительным z = x. Два комплексных числа z1 = x1 + jy1 и z2 = x2 + jy2 называются равными (z1 = z2), тогда и только тогда, когда равны их действительные и мнимые части (х1 = х2, у1 = у2). Понятие сравнения (больше-меньше) для комплексных чисел не вводится. Два комплексных числа z = x + jy и Геометрическое изображение комплексных чисел Комплексная плоскость Рассмотрим на плоскости декартову прямоугольную систему координат. Каждому комплексному числу z = x + jy можно сопоставить точку с координатами (х, у), и наоборот, каждой точке с координатами (х, у) можно сопоставить комплексное число z = x + jy. Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, называют комплексной плоскостью. Например, изобразим на комплексной плоскости числа z1 = 2 + j, z2 = 3j, z3 = -3 + 2j, z4 = - 1 -j:
Изображение комплексных чисел точками плоскости Однако, чаще комплексные числа изображают в виде вектора с началом в точке О, а именно, комплексное число z = x + jy изображается радиус-вектором точки с координатами (х, у). В этом случае изображение комплексных чисел из предыдущего примера будет таким:
Изображение комплексных чисел радиус-векторами Пусть комплексное число z = a + jb изображается радиус-вектором. Длина этого вектора называется модулем числа z и обозначается |z|. Из рисунка очевидно, что
Модуль и аргумент комплексного числа Угол, образованный радиус-вектором числа z с осью Ox, называется аргументом числа z и обозначается arg z . Аргумент числа определяется не однозначно, а с точностью до числа, кратного 2π . Однако, обычно аргумент указывают в диапазоне [-π; π] и называют это значение главным значением аргумента. У числа z = 0 аргумент не определен. На рисунке arg z равен углу φ . Из того же рисунка очевидно, что
С помощью этого соотношения можно находить аргумент комплексного числа:
arg z = arctg (b/a) - π - если изображение числа z находится в третьей четверти. Пример:найти модуль и аргумент числа z = -1 + j:
Тригонометрическая форма комплексного числа Запись числа в виде z = x + jy называется алгебраической формойкомплексного числа. Используя выражения для модуля и аргумента:
можно записать z = |z|(cos φ + j∙sin φ). Такая запись называется тригонометрической формой комплексного числа. Например, запишем в тригонометрической форме число z = 2 + 2j:
Поиск по сайту: |
 , отличающиеся лишь знаком мнимой части, называются сопряженными.
, отличающиеся лишь знаком мнимой части, называются сопряженными.

 .
.
 ;
; 
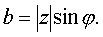
 - если изображение числа z находится в первой или четвертой четверти;
- если изображение числа z находится в первой или четвертой четверти; - если изображение числа z находится во второй четверти;
- если изображение числа z находится во второй четверти; ;
; (число находится во II четверти).
(число находится во II четверти).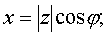

 - модуль числа;
- модуль числа; - аргумент числа (главное значение);
- аргумент числа (главное значение); - тригонометрическая форма комплексного числа.
- тригонометрическая форма комплексного числа.