 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Билет №18 Итерационные методы решения систем линейных алгебраических уравнений. Метод простой итерации ⇐ ПредыдущаяСтр 7 из 7
Пусть дана система n линейных уравнений с n переменными: а11x1+a12+…+a1nxn=b1 а21x1+a22+…+a2nxn=b2 (1) ……………………… an1x1+an2+…+annxn=bn с/ п равносильных преобразований приведем эту систему к виду: x1=ά12* x2+…+ ά1n * xn+ß1 (2) x2=ά22* x2+…+ ά2n * xn+ß2 …………………………….. xn=άn2* x2+…+ άnn * xn+ ßn о ситеме 2 говорят, что она приведена к норм.виду
x0(
x0, x1,x2, … , xn,...(3) при определенных условиях итерационная последовательность 3 сходиться к решению системы 2 и тем самым системы 1. Сформулируем эти условия. Решение этого вопроса зависит от способа метризации пространства, т.е определения расстояния между двумя его точками. Существует несколько способов метризации.
1) 1 ≤ i ≤ n 2)
3)
Условия сходимости последовательности 3 в пространствах с метриками ρ1, ρ2, ρ3выражается через коэффициенты αij. 1. В пространстве с метрикой ρ1: γ1 = max 1 ≤ i ≤ n Т.еmax из сумм модулей коэффициентов 2. С метрикой ρ2: γ2 = max 1 ≤ i ≤ n Т.еmax из сумм модулей коэффициентов 3. С метрикой ρ3: γ3 = т.е корень из суммы квадратов всех коэффициентов должны быть меньше 1. Замечание: Каждая из условий (7)-(9) является достаточным, но не является необходимым для результативности метода итераций, т.е итерационная последовательность 3 может оказаться сходящейся и при не выполнение не одного из этих уловий. Для обеспечения условий сходимости нужно получить систему вида 2 так, чтобы коэффициенты Результатом установления одного из условий (7)-(9) является получение значения γ которое затем используется для оценки погрешности: ρ (x(k); x(k-1)) ≤ Практика по методу простой итерации: Решить систему методом простой итерации
α21 =3; α22 = 0; α23= α31 =2; α32 = 16; α33 = 0 ;β3 = - 5; т.к для этого систему 1 приводим к виду с преобладающими диагональными коэффициентами:
α11 =0; α12 = α21 = α31= γ1<1; γ2<1; γ3<1; γ1 = γ2= γ3=
x3(1) = ρ (x(k); x(k-1)) ≤ ρ1 (x(k); x(k-1)) ≤ ρ1 (x(1); x(0))≤ max
Ответ: корень уравнения с заданной точностью (x1=5/24;x2=55/192;x3= -31/192)
ρ1 = max
Поиск по сайту: |
 используя правую часть норм.системы 2 и выбрав начальную точку:
используя правую часть норм.системы 2 и выбрав начальную точку: ;
;  ;
;  ; …;
; …;  ) – начальная точка.
) – начальная точка.
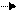
 Можно построить итерационную последовательность точек:
Можно построить итерационную последовательность точек:

 Пусть x(x1, x2,...,xn) и y (y1, y2,…, yn) две точки пространства для применения метода простой итерации СЛАУ удобно поместить в пространство с одной из 3- х метрик:
Пусть x(x1, x2,...,xn) и y (y1, y2,…, yn) две точки пространства для применения метода простой итерации СЛАУ удобно поместить в пространство с одной из 3- х метрик:
 ρ1(x ,y) = max
ρ1(x ,y) = max  (4)
(4)
 ρ2(x ,y) =
ρ2(x ,y) =  (5) евклидова метрика
(5) евклидова метрика
 ρ3(x ,y) =
ρ3(x ,y) =  (6)
(6) (7)
(7) взятых по строкам должны быть меньше 1.
взятых по строкам должны быть меньше 1. (9)
(9) .
. (10), где ρ – метрика по которой была установлена сходимость и выбрано значение γ.
(10), где ρ – метрика по которой была установлена сходимость и выбрано значение γ.
 (2)
(2)
 ; β2 =
; β2 =  ;
;
 (2)
(2) ; α13 =
; α13 =  ; β1 =
; β1 =  ;
; ; α22 = 0; α23=
; α22 = 0; α23=  ; β2 =
; β2 =  ;
; ; α32 =
; α32 =  =
=  {
{ 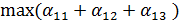 }
} =
=  {
{  }
} =
= 



 т.к для всех γ; выполняется условие γ<1, то для критерия сходимости мы можем выбрать любую γ и соответствующую ей метрику; выберем γ1 в качестве начальной точки выберем столбец ρ; x(0) =
т.к для всех γ; выполняется условие γ<1, то для критерия сходимости мы можем выбрать любую γ и соответствующую ей метрику; выберем γ1 в качестве начальной точки выберем столбец ρ; x(0) =  ,для нахождения точки x(1) воспользуемся системой вида 2 в которую подставим значение x(0)
,для нахождения точки x(1) воспользуемся системой вида 2 в которую подставим значение x(0) x1(1) =
x1(1) = 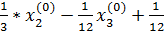 =
=  =
= 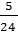 ;
; x2(1) =
x2(1) =  =
= 


 =
=  =
= 

 ( + )
( + ) Если неравенство оказалось неверным, то находим следующее приближение x2(
Если неравенство оказалось неверным, то находим следующее приближение x2(  ;
;  ;
;  ).
).

 ρ1 (x(2); x(1)) ≤
ρ1 (x(2); x(1)) ≤ 