 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Билет №3 Численное решение нелинейных уравнений с одной переменной. Метод половинного деления
Пусть уравнение F(x)=0 имеет на [a;b] единственный корень, причем функция F(x) на этом отрезке непрерывна. Разделим отрезок [a;b] и пополам точкой с=(a+b)/2. Если F(c) =/=0, то возможны 2 случая: либо F(x) меняет знак на [a;c], либо на отрезке [c;b]. Выбирая в каждом случае тот из отрезков, на котором функция меняет знак и продолжая процесс половинного деления дальше можно дойти до сколь угодно малого отрезка содержащего корень уравнения. Метод половинного деления по-другому называют метод бисекции или дихотомии. Этот метод можно использовать как метод решения уравнения с заданной точностью. Если на каком то этапе процесса получен отрезок [a,b], содержащий корень, то приняв приближенно значение корня x = (a+b)/2 получим ошибку не превышающую ∆x=(b-a)/2 (2).
F(b)>0
F(c)
F(a)<0
Пусть нам дана точность ε=0.001. Процесс решения (половинного деления) продолжается до тех пор, пока не выполнится неравенство ∆х ≤ε (3) ∆х – половина отрезка АВ. Билет №4 Алгоритм решения задачи методом половинного деления
Билет №5 Программная реализация метода половинного деления Program PI38; Function f (z: real): real; Begin f:=sin (sgr(z)); End; Var a,b,c,d,e: real; Begin Writeln (‘введитеотрезок [a; b]'); Readln (a,b); Writeln (‘введитеэпсилоне’); Readln (e); Repeat c:=(a+b)/2; If F(a)*F(c)<0 then b:=c else a:=c; d:=(b-a)/2; Until d<=e; Writeln (“Корень =”, с, “c точностью Δx = “, d); Readln; End. Билет №6 Численное решение нелинейных уравнений с одной переменной. Метод хорд Методы Ньютона Рассмотрим 2 метода Ньютона: метод касательных и метод хорд. Оба метода основаны на следующем приеме. Пусть уравнение F(х)=0 имеет единственный корень на отрезке [a, b] (1) Преобразуем его к равносильному уравнению х=х-j(х)*F(x) (2), где j(х) – любая функция, определенная на отрезке [a, b] и не обращающаяся на нем в ноль. Метод хорд (МХ) x=х-j(х)*F(c) Пусть φ(х)= тогда формула для метода хорд примет вид х=х- xn=xn-1- Функция F(x) удовлетворяет следующим условиям: 1) является дважды дифференцируемой на отрезке [a, b] 2) обе производные не меняют знак на этом отрезке, т.е. f(x) монотонна и не имеет характера выпуклости. В качестве точкиС выбирается тот конец [a, b] , для которого выполняется условие F(c)*F”(c)>0 (4) В качестве х0 берется тот конец отрезка [a, b], который остался после выбора с.
b(x0)
a (c)
ξ a(x0) x1 b(c) F (a) < 0, F (b) >0, F” >0
a(x0) ξ b(c)
Пусть уравнениех = х - D хn≤ e Dхn= Алгоритм решения уравнения методом хорд 1) выбор точки С F(c)*F”(c)>0 2) выбор точки х0 3) х1= х0 - Dx1= -: 4 4) х2=х1-
Поиск по сайту: |




 0 acbх
0 acbх




 + -
+ -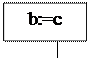







 - +
- +

 (1)
(1) *F(x) (2)
*F(x) (2) *F(xn-1) (3) n=1, 2…
*F(xn-1) (3) n=1, 2…


 F(x0) F (a) < 0, F (b) > 0, F”< 0
F(x0) F (a) < 0, F (b) > 0, F”< 0

 a (c)
a (c)
 F(c) ξ x1b(x0)
F(c) ξ x1b(x0)






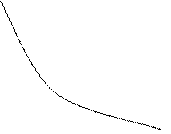 F (a) > 0, F (b) < 0, F” > 0
F (a) > 0, F (b) < 0, F” > 0
 ξ x2 x1
ξ x2 x1



 F (a) > 0, F (b) < 0, F” < 0
F (a) > 0, F (b) < 0, F” < 0




 * F(x) решается методом хорд, причем результат должен быть получен с точностью e. Критерием прекращения вычисления при достижении заданной точности является условие:
* F(x) решается методом хорд, причем результат должен быть получен с точностью e. Критерием прекращения вычисления при достижении заданной точности является условие: где m - min |F¢(x)| на [a, b]
где m - min |F¢(x)| на [a, b]
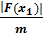 Dx1≤e? +: ответ х1, Dх1
Dx1≤e? +: ответ х1, Dх1 Dx2=
Dx2=  Dx2≤e? +: ответ х2, Dх2 -: х3, …
Dx2≤e? +: ответ х2, Dх2 -: х3, …