 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Степень с целым показателемСтр 1 из 5Следующая ⇒
Множество рациональных чисел. Множество действительных чисел. Множество (Q) рациональных чисел Объединение множества целых и дробных чисел есть множество рациональных чисел. Свойства множества рациональных чисел (Q) 1.Замкнуто относительно операций сложения, вычитания, умножения, деления. 2. Упорядоченно: для любых рациональных чисел можно установить отношение порядка (a>b, a<b, a = b). 3. Плотно в себе: для любых двух рациональных чисел a и b (a < b) всегда найдётся такое рациональное число c, что a < c < b. 4. Обладает свойством Архимеда: для любого рационального числа a существует такое целое число n, что n £ a < n+1. Множество действительных чисел Объединение множества рациональных и иррациональных чисел есть множество действительных чисел. Доказать, что не существует рационального числа, квадрат которого равен 2.
Степень с натуральным показателем Определение: Степенью числа a с натуральным показателем n (n > 1) называется произведение n множителей, каждый из которых равен a.
Свойства степени с натуральным показателем (m, n ÎN): 1) 2) 3) 4) 5) 6) если a > 0, то 7) если a > 1, то 8) если 0 < a < 1, то 1) 2) 3)
7. Степени с натуральным, целым и рациональным показателями. Корень n-ой степени. Арифметический корень Степень с целым показателем Степенью с целым показателем(–n), где nÎN действительного числа a, отличного от 0, называют число, обратное степени числа a с показателем n, т.е. a0 = 1, если a ¹ 0. Выражения Свойства степени с целым показателем (a, bÎR\{0}, s, tÎZ): 1) 2) 3) 4) 5) 6) если a > 0, то 7) если a > 1, s > 0, то 8) если 0 < a < 1, s > 0, то
Доказательство : 1) Аналогично доказываются свойства 2 – 5. 2) 3) 4) 5) 6) Допустим противное:
Корень нечётной степени из отрицательного действительного числа находится следующим образом:
Поиск по сайту: |
.
, обозначают 
. Число a называется основанием степени. 
;
, m > n; 
;
;
;; 
;
;
.
.
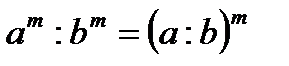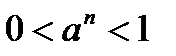. Согласно свойству 1): 
. По определению деления это означает, что 
.
= 
= 
= 
.
.
, 
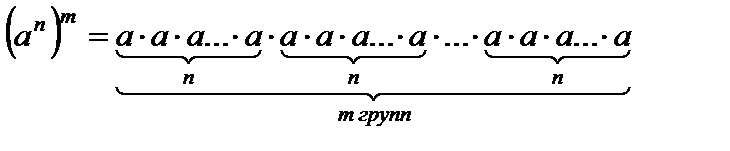, где 
не определены.
;
;
;
;
;
;
; если a > 1, s < 0, то 
;
; если 0 < a < 1, s < 0, то 
.
– неотрицательное число, n-я степень которого равна ab, т.е 
=ab. Число 
неотрицательно, т.к. по определению 
и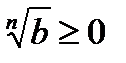 
. Вычислим n-ю степень числа 
= 
. Следовательно, 
, что и требовалось доказать.
и 
; 
, 
, значит, 
.
и 
; 
и 
, значит, 
.
и 
; 
и 
, значит, 
.
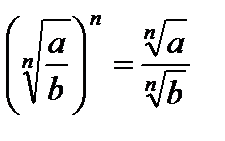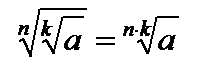и 
; 
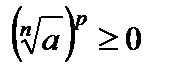, так как 
и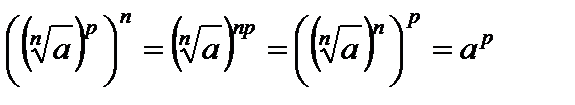 
, значит, 
.
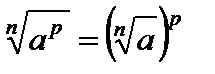, тогда по свойству степеней с натуральным показателем 
, т.е 
, что противоречит условию 
, значит, предположение не верно.
. При a = 0 
=0