|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Ряд Фурье для непериодических функций ⇐ ПредыдущаяСтр 5 из 5
Ранее было показано, что в ряд Фурье разлагаются только периодические функции с периодом Если функция Возможны следующие случаи: 1. Если функция 2. Если функция 3. Если функция
Элементы гармонического анализа Разложение периодической функции в ряд Фурье называется гармоническим анализом. Рассмотрим слагаемые ряда Фурье. Значение Первое непостоянное слагаемое называется основной гармонической, оно имеет период Остальные слагаемые называются верхними гармониками, их наименьшие периоды равны Если независимая переменная рассматривается как время, то ряд Фурье описывает произвольное периодическое колебание в виде суммы гармонических колебаний с кратными частотами. Например, в акустике: основное слагаемое определяет высоту звука, т. е. основной тон; остальные слагаемые описывают обертоны, от которых зависит тембр звука. Ряды Фурье используются в решении задач математической физики, а также их применяют при изучении различных зависимостей в электрических цепях с несинусоидальными токами.
Поиск по сайту: |
 или
или  , т. к. функции
, т. к. функции  и
и  периодические.
периодические. не является периодической, то, чтобы разложить ее в ряд Фурье, строят некоторую периодическую функцию
не является периодической, то, чтобы разложить ее в ряд Фурье, строят некоторую периодическую функцию  , которая в области определения функции совпадает с функцией
, которая в области определения функции совпадает с функцией  . В этом случае говорят, что функцию
. В этом случае говорят, что функцию 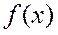 периодически продолжают на всю числовую ось.
периодически продолжают на всю числовую ось. задана на
задана на  , то строят функцию
, то строят функцию  с периодом
с периодом  . Она на отрезке
. Она на отрезке 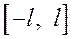 совпадает с функцией
совпадает с функцией 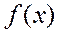 , а на остальной части числовой оси является ее периодическим продолжением.
, а на остальной части числовой оси является ее периодическим продолжением.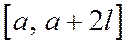 , то строят
, то строят 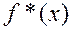 с периодом
с периодом  , которая на отрезке
, которая на отрезке 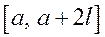 совпадает с функцией
совпадает с функцией  и
и  .
. задана на отрезке
задана на отрезке  , то для разложения в ряд Фурье достаточно ее доопределить на отрезке
, то для разложения в ряд Фурье достаточно ее доопределить на отрезке 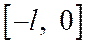 произвольным способом. Затем разложить в ряд Фурье, считая ее заданной на отрезке
произвольным способом. Затем разложить в ряд Фурье, считая ее заданной на отрезке 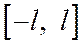 . Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках отрезка
. Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках отрезка 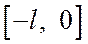 находились из условия
находились из условия  или
или 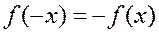 . В первом случае функция
. В первом случае функция  на отрезке
на отрезке 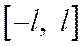 будет четной, а во втором – нечетной. При этом коэффициенты разложения такой функции (
будет четной, а во втором – нечетной. При этом коэффициенты разложения такой функции (  в первом случае,
в первом случае, 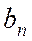 – во втором) можно определить по вышеперечисленным формулам для коэффициентов четных и нечетных функций.
– во втором) можно определить по вышеперечисленным формулам для коэффициентов четных и нечетных функций. равно среднему значению функции
равно среднему значению функции 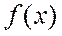 на всей оси.
на всей оси. .
.