 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства периодической функции
1) Сумма, разность, произведение и частное периодических функций периода 2) Если функция 3) Если Ряды Фурье (Фурье – французский математик и физик 1768–1830) используются для описания периодических процессов, решения дифференциальных уравнений, приближения периодических и непериодических функций. В этих случаях функцию, описывающую периодический процесс, представляют как сумму простых периодических функций Полагая
Сложные процессы описываются функциями вида
Выражение вида Основная тригонометрическая система функций:
10.Достаточные признаки разложимости функции в ряд Фурье Определение. Точка Теорема Дирихле. Если на отрезке 1) в точках непрерывности функции 2) в каждой точке разрыва 3) в обеих граничных точках отрезка
11. Ряд Фурье для периодической функции с периодом Тригонометрический ряд
называется тригонометрическим рядом Фурье для периодической функции
Пример. Разложить в ряд Фурье периодическую функцию f(x) с периодом Т = 2l, которая на отрезке Решение. Найдем коэффициенты ряда Фурье:
12. Ряд Фурье для периодической функции с периодом Ряд Фурье для такой функции получается из ряда 1 при значении
Пример.Разложить в ряд Фурье функцию, заданную в промежутке Решение.Графиком этой функции является отрезок, соединяющий точки
Эта функция является периодической с периодом Определяем коэффициенты ряда Фурье. Сначала находим
Второй интеграл равен нулю как интеграл от нечетной функции, взятый по интервалу, симметричному относительно начала координат. Таким образом, Далее находим коэффициенты
Оба интеграла равны нулю, т. к. подынтегральная функция второго интеграла является нечетной как произведение четной и нечетной функций. Итак, Определяем теперь коэффициенты
Первый интеграл равен нулю. Подынтегральная функция второго интеграла – четная как произведение двух нечетных функций. Таким образом, Решим данный интеграл, интегрированием по частям:
Следовательно, разложение функции
Поиск по сайту: |
 есть периодическая функция периода
есть периодическая функция периода  .
.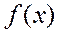 период
период 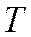 , то функция
, то функция  имеет период
имеет период  .
. – периодическая функция периода
– периодическая функция периода  , то равны любые два интеграла от этой функции, взятые по промежуткам длины
, то равны любые два интеграла от этой функции, взятые по промежуткам длины 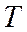 (при этом интеграл существует), т. е. при любых
(при этом интеграл существует), т. е. при любых  и
и  справедливо равенство
справедливо равенство 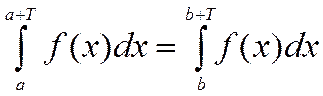 .
. ,
,  –амплитуда,
–амплитуда,  –фаза колебаний,
–фаза колебаний,  – начальная фаза.
– начальная фаза.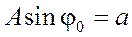 ,
,  , можно записать
, можно записать .
. .
. , где
, где  – основная тригонометрическая система функций, называется тригонометрическим рядом Фурье.
– основная тригонометрическая система функций, называется тригонометрическим рядом Фурье. , определена на отрезке
, определена на отрезке  , где
, где  – период функции. Числа
– период функции. Числа  называются коэффициентами Фурьефункции
называются коэффициентами Фурьефункции  .
. разрыва функции
разрыва функции  функция
функция  имеет конечное число точек разрыва первого рода (или непрерывна) и конечное число точек экстремума (или не имеет их вовсе), то ее ряд Фурье сходится, т. е. имеет сумму
имеет конечное число точек разрыва первого рода (или непрерывна) и конечное число точек экстремума (или не имеет их вовсе), то ее ряд Фурье сходится, т. е. имеет сумму  , во всех точках этого отрезка. При этом:
, во всех точках этого отрезка. При этом: он сходится к самой функции
он сходится к самой функции  ;
; функции сходится к полусумме односторонних пределов функции справа и слева
функции сходится к полусумме односторонних пределов функции справа и слева  ;
;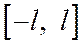 сходится при стремлении величины
сходится при стремлении величины  к этим точкам изнутри отрезка к полусумме односторонних пределов функции
к этим точкам изнутри отрезка к полусумме односторонних пределов функции  .
.
 (1)
(1) , если коэффициенты его определяются по формулам:
, если коэффициенты его определяются по формулам: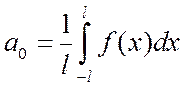 ,
, , где
, где  ,
, , где
, где  .
. задана равенством
задана равенством  .
.



 .
. .
. , т. к.
, т. к.  , то разложение примет вид
, то разложение примет вид  , следовательно, искомое разложение имеет вид:
, следовательно, искомое разложение имеет вид: .
.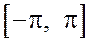
 .
. , где
, где
 ,
, 
 ,
, 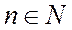
 уравнением
уравнением 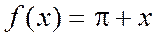 .
. и
и  . На рисунке показан график функции
. На рисунке показан график функции  .
.
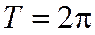 .
. .
. .
. :
: .
. , т. е.
, т. е.  .
. :
: .
. .
.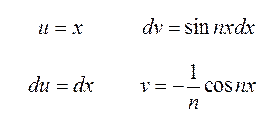 , т. е.
, т. е. 

 .
. в ряд Фурье имеет вид:
в ряд Фурье имеет вид: .
.