 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Второй признак сравнения (предельный признак)
Если Следствие. При применении 2-го признака сравнения удобно брать в качестве ряда, с которым сравнивается данный ряд, ряд вида Признак Даламбера
Пусть для ряда Тогда этот ряд сходится при значении L
Пример. Определить сходимость ряда
Вывод: ряд сходится. Радикальный признак Коши
Если для ряда Так же, как в признаке Даламбера, L = 1 не дает ответа на вопрос о сходимости ряда. Пример. Определить сходимость ряда
Вывод: ряд сходится.
Интегральный признак Коши Если функция Знакочередующиеся ряды Определение. Если два стоящих рядом члена ряда имеют разные знаки, то ряд называется знакочередующимся. Его вид: Вопрос о сходимости знакочередующегося ряда решается с помощью следующего признака. Теорема (признак Лейбница). Если члены знакочередующегося ряда 1) 2) Пример. Ряд 1- 1) 1…; 2) Замечание. Если хотя бы одно условие признака Лейбница не выполняется, то ряд расходится. Применение сходящихся рядов к приближенным вычислениям основано на замене суммы ряда суммой его нескольких первых членов. Допускаемая при этом погрешностьоценивается для знакочередующегося ряда по признаку Лейбница. Следствие. Погрешность суммы сходящегося знакочередующегося ряда при приближенном вычислении по абсолютной величине меньше абсолютного значения первого из отброшенных членов ряда: Абсолютная и условная сходимость знакопеременного ряда
Поиск по сайту: |
 и
и 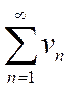 – ряды с положительными членами и существует конечный предел отношения их общих членов
– ряды с положительными членами и существует конечный предел отношения их общих членов  , то ряды одновременно сходятся либо расходятся.
, то ряды одновременно сходятся либо расходятся. .
.
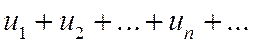 существует предел
существует предел  .
. и расходится при значении L
и расходится при значении L  . При значении L=1 вопрос о сходимости ряда остается открытым, поэтому необходим другой признак.
. При значении L=1 вопрос о сходимости ряда остается открытым, поэтому необходим другой признак.
 ;
;  ;
;  =
= 

 существует предел
существует предел  , то при значении
, то при значении  ряд сходится, при значении
ряд сходится, при значении  – расходится.
– расходится. .
.
 непрерывна, монотонно убывающая при значении
непрерывна, монотонно убывающая при значении  и такая, что
и такая, что 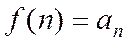 при значении
при значении  , где
, где  – члены ряда
– члены ряда  , то данный ряд сходится или расходится, в зависимости от сходимости несобственного интеграла
, то данный ряд сходится или расходится, в зависимости от сходимости несобственного интеграла  .Например, обобщённый гармонический ряд 1+
.Например, обобщённый гармонический ряд 1+  … сходится при α
… сходится при α  , потому что
, потому что  сходится при α
сходится при α 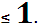
 .
. удовлетворяют условиям:
удовлетворяют условиям: ,
,  , т. е. члены ряда не возрастают (убывают) по абсолютной величине;
, т. е. члены ряда не возрастают (убывают) по абсолютной величине; , то данный ряд сходится, а его сумма не превосходит первого члена ряда, т. е.
, то данный ряд сходится, а его сумма не превосходит первого члена ряда, т. е.  .
. сходится, т. к.
сходится, т. к.
 .
.