 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Ковариационная матрица линейного преобразования ⇐ ПредыдущаяСтр 5 из 5
случайного вектора. Следующая теорема данного цикла расширяет наши возможности на случай, когда исследуется не одна функция случайного вектора, а целая линейная вектор-функция случайноговектора: Ym1 = Cmn∙ Xn1, (131) ковариационная матрица которого KX – известна. Представим эту теорему в форме задачи по нахождению ковариационной матрицы линейного преобразования случайного вектора. Дано: Ym1 = Cmn∙Xn1 – линейное преобразование вектора Xn1; KX={Kij} – ковариационная матрица преобразуемого вектора, элементы которой Kij определяются формулой (100). Найти: Ковариационную матрицу KY – ? Решение: Опираясь на матричное определение (102) ковариационной матрицы произвольного случайного вектора, можем написать: KY= E{(Ym1 – E(Ym1)) ∙ (Ym1 – E(Ym1))T}. (132) Подставив в (132) вместо вектора Ym1 его зависимость (131) от вектора Xn1 и опустив индексы размерностей векторов, получим такой результат: KY = E((CX – E(CX)) ∙ (CX – E(CX))T) = = E(C(X – E(X)) ∙ (X – E(X))TCT) = = C ∙ E((X – E(X)) ∙ (X – E(X))T) ∙ CT. Поскольку E((X – E(X)) ∙ (X – E(X))T) = KX, окончательно записываем: KY= C ∙ KX ∙ CT. # (133) Формула (133) была опубликована А. Эйткиным в 1935 г. [9]. В качестве Упражнения 2.3 докажите, что формула (115) – это частный случай (133), когда m= 1. Задача 2.15. Два смежных угла y1 и y2 вычислены как разности соседних некоррелированных и равноточно измеренных направлений x1, x2 и x3, т.е. y1 = x2 – x1 и y2 = x3 – x2. Найти коэффициент корреляции этих углов. Дано: Y21T = Найти: Решение: Вектор углов Y21 является линейным преобразованием вектора направлений X31. Матрица преобразования C23 находится по связям, описанным в тексте задачи: C23= Окончательно, преобразование принимает вид:
Формула (133) позволяет найти ковариационную матрицу углов: KY = σ2 На основании соотношения (99), с одной стороны, K12 = ρ12 ∙ σ1∙σ2, где K12 = – σ2. Таким образом, K12 = ρ12 ∙ σ1 ∙ σ2 = ρ12 ∙ 2 σ2 = – σ2. Отсюда легко определяется искомый коэффициент корреляции смежных углов: ρ12 = – σ2/ 2 σ2 = – 0,5. # 2.3.5.7 Ковариационная матрица преобразования случайного вектора с помощью дифференцируемой вектор-функции. Преобразование случайного вектора Xn1, характеризующегося ковариационной матрицей KX, в новый случайный вектор Ym1 с помощью дифференцируемой вектор-функции Fm1 будет иметь свою ковариационную матрицу KY. Найдем её. Дано: Ym1 = Fm1(Xn1) – преобразование вектора Xn1 с помощью дифференцируемой вектор-функции Fm1; KX – ковариационная матрица случайных аргументов. Найти: KY – ? Решение: По определению (102) вновь имеем KY= E{(Ym1 – E(Ym1)) ∙ (Ym1 – E(Ym1))T}. (134) Разложив вектор-функцию Ym1 = Fm1(Xn1) в окрестности точки E(Xn1) в ряд Тейлора и ограничившись линейными членами (помня, что Xn1=E(Xn1)+ Ym1 = Fm1(E(Xn1) + Здесь, согласно [10], {∂F/∂X}mn= fmn– дифференциальный оператор, представляющий собой матрицу частных производных, в каждой из m строк которой стоят n частных производных по каждому из n аргументов: fmn = Найдем теперь МО этой функции: E(Ym1) ≈ E(Fmn(E(Xn1)) + fmn∙ E(Ym1) ≈ F(E(Xn1)), (136) т.к. E( Вычитая из (135) выражение (136), находим центрированный вектор
и, используя определение (102), находим интересующую нас ковариационную матрицу KY произвольного преобразования случайного вектораXn1: KY=E( KY ≈ fmn∙KX∙fnmT # (138) Это и есть искомая приближенная связь между ковариационной матрицей KX случайного вектора Xn1 и ковариационной матрицей KY его произвольного преобразования Ym1 = Fm1(Xn1). Доказать в качестве Упражнения 2.4, что формула (122) является частным случаем соотношения (138), когда m= 1. Задача 2.16. Приращения прямоугольных координат геодезического пункта Δx и Δy вычислены по независимым аргументам: расстоянию s и дирекционному углу a. Полагая известными стандарты аргументов σs и σα, найти ковариационную матрицу приращений координат K∆ и установить, при каких относительных значениях стандартов аргументов s и aэти приращения будут не коррелированы. Дано: Δx = s ∙ cosa; Δy = s ∙ sina; σs; σα. Найти: а) K∆ – ?; б) соотношение между σs и σα, при котором Kxy= 0. Решение: Запишем, прежде всего, нелинейное преобразование расстояния s и дирекционного угла a в приращения координат Δx и Δy в матричном виде:
Составим матрицу частных производных f22приращений координат Δx и Δyпо расстоянию s и дирекционному углу a: f22= Ковариационная матрица некоррелированных аргументов, как это следует из условий задачи, должна быть диагональной: Ks,a= Теперь мы можем найти ковариационную матрицу K∆ приращений координат, выполнив преобразования по формуле (138): K∆ = = Это – ответ на первый вопрос задачи. Что же касается ответа на второй вопрос, то для его получения необходимо приравнять нулю элемент K12 только что полученной матрицы: K12 = 0,5 а затем, заменить в нем приращения координат их выражениями через расстояние s и дирекционный угол a: 0,5 Отсюда мы сразу находим искомое соотношение между стандартами линииσs и и дирекционного углаσα, при котором приращения абсциссы Δx и ординаты Δy не будут коррелированы: σs/ s= σα, т.е. относительный стандарт линии должен равняться стандарту дирекционного угла, выраженному в радианной мере. Отметим, что при этих условиях и сами стандарты приращений Убедитесь в этом в качестве Упражнения 2.5.
Поиск по сайту: |
 ; X31T =
; X31T =  ; KX = σ2I33, т.к. измерения некоррелированные (Kij= 0
; KX = σ2I33, т.к. измерения некоррелированные (Kij= 0  ) и равноточные (
) и равноточные ( = σ2), где σ2 – дисперсия направлений.
= σ2), где σ2 – дисперсия направлений. = ρ12 – ?
= ρ12 – ?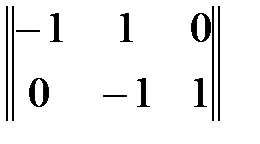 .
. =
=  ∙
∙  .
.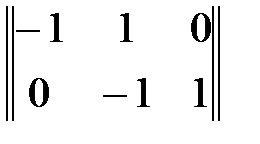 ∙
∙ 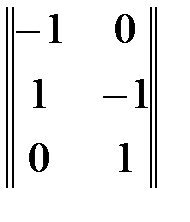 = σ2
= σ2 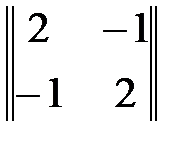 =
=  .
. = K11 =
= K11 =  = K22 = σ2, а с другой стороны:
= K22 = σ2, а с другой стороны: n1), получим:
n1), получим: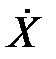 n1) ≈ Fm1(E(Xn1)) + {∂F/∂X}mn∙
n1) ≈ Fm1(E(Xn1)) + {∂F/∂X}mn∙  n1. (135)
n1. (135) .
. n1) = Fmn(E(Xn1)) + fmn∙E(
n1) = Fmn(E(Xn1)) + fmn∙E(  n1)) →
n1)) → n1) = 0n1, как вектор центральных моментов первого порядка.
n1) = 0n1, как вектор центральных моментов первого порядка. n1 = Ym1 – E(Ym1)
n1 = Ym1 – E(Ym1)  fmn∙
fmn∙  n1 (137)
n1 (137) n1∙
n1∙  1nT} ≈ E(fmn
1nT} ≈ E(fmn  n1∙
n1∙  fnmT) = fmn∙E(
fnmT) = fmn∙E( 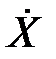 n1
n1  )∙fnmT.→
)∙fnmT.→ =
=  .
. =
=  .
. .
. =
= 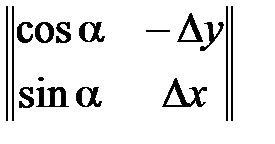 ∙
∙ 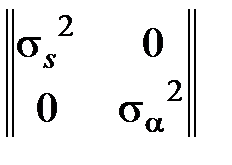 ∙
∙  =
= .
. ∙ sin2α –
∙ sin2α –  ∙ Δx Δy = 0,
∙ Δx Δy = 0, ∙ sin2α = 0,5
∙ sin2α = 0,5  =
=  и
и 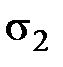 =
=  упростятся и будут равными друг другу и стандарту линии ss.
упростятся и будут равными друг другу и стандарту линии ss.