 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Классификация изолированных особых точек ⇐ ПредыдущаяСтр 3 из 3
Определение 8.Точка z0 называется правильной (регулярной) точкой функции f(z), если во всякой окрестности этой точки функция аналитическая. Определение 9.Точка z0 называется особой точкой функции f(z), если ни в какой окрестности этой точки функция не является аналитической. Примерами особых точек являются точки, в которых функция обращается в бесконечность, либо производной не существует или производная равна бесконечности. Будем рассматривать однолистные функции. У таких функций особыми точками являются точки, в которых f(z) обращается в бесконечность, где она неопределенна или не дифференцируема. Определение 10.Изолированной особой точкой однозначного характера называют точку z0 ,в проколотой окрестности которой f(z) является аналитической. Это означает, что в области 0<|z-z0|< Пример 6.Рассмотрим функцию f(z)= При Точка z0=0 тоже является особой, но не является изолированной, т.к. является сгущением особых точек zk= Проколотая окрестность 0<|z-z0|<ε представляет собой кольцо с внутренним радиусом r=0, поэтому в этом кольце f(z) может быть представлено рядом Лорана (9). Определение 11.Изолированная особая точка однозначного характера z0 функции f(z) называется: а) устранимой особой точкой, если разложение f(z) проколотой окрестности точки z0 не содержит слагаемых с отрицательными степенями z, т.е.
б) полюсом m-го порядка, если разложение ряда Лорана содержит конечное число слагаемых с отрицательными степенями, т.е. f(z)= в) существенно особой точкой, если разложение в ряд Лорана содержит бесконечное число слагаемых с отрицательными степенями f(z)= Пример 8.Определить характер особой точки z=0 для следующих функций: а) f(z)= Разложение в ряд Лорана имеет вид:
Таким образом, z=0 есть полюс первого порядка. б) f(z)= Разложение в ряд Лорана имеет вид: ez= и, таким образом, z=0 - существенно особая точка. Теорема 13. (необходимое и достаточное условие существования устранимой особой точки) Для того, чтобы точка z0 была устранимой точкой функции f(z) необходимо и достаточно, чтобы функция f(z) была аналитической и ограниченной в некоторой проколотой окрестности точки z0. □ Необходимость. Пусть z0-устранимая особая точка, тогда в некоторой проколотой окрестности 0<|z-z0|<R функция будет аналитической и ее можно разложить в ряд Лорана, причем он не будет содержать отрицательных степеней z:
Тогда
т.е. предел в точке z0 существует и следовательно f(z) ограничена в этой проколотой окрестности. Достаточность. Пусть функция f(z) аналитическая в проколотой окрестности и существует M,такое, что |f(z)|≤M при 0<|z-z0|<R. В этом кольце f(z) можно разложить в ряд Лорана, коэффициенты которого задаются равенством:
Оценим коэффициенты ряда Лорана по модулю: cn|=| Коэффициенты ряда Лорана не зависят от r, поэтому, если вычислить
Т.о., из последнего следует, что для n<0 коэффициенты ряда Лорана тождественно равны нулю, т.е. ряд не имеет слагаемых с отрицательными степенями. Это по определению означает, что z0 устранимая особая точка. ■ Замечание.Пусть z0 устранимая особая точка и f(z)=φ(z)(z-z0)m, где φ(z0)≠0, а z0 является нулем m-го порядка функции f(z). Теорема 14(необходимое и достаточное условие полюса). Для того, чтобы точка z0 была полюсом функции f(z) необходимо и достаточно, чтобы функция f(z) была аналитической в проколотой окрестности точки z0 и при z→z0 произвольным образом |f(z)|→∞. □ Необходимость. Пусть z0 полюс f(z) m-го порядка, тогда по определению имеет место разложение: f(z)= Приведем к общему знаменателю
В числителе стоит степенной ряд, который является некоторой функцией φ(z), причем φ(z0)=с-m Переходя к пределу в левой и правой части
Достаточность. Пусть f(z) неограниченная функция при z→z0, но является аналитической в проколотой окрестности точки z0. Ограниченность означает, что g(z)= φ(z)(z-z0)m, φ(z0)≠0. Т.о. для функции f(z) будем иметь: f(z)= Функция Теорема 15.(Сохоцкого-Вейерштрасса) Каково бы ни было ε>0 в любой окрестности существенно-особой точки z0 функции f(z) найдется хотя бы одна точка z1, в которой значение f(z) отличается от любого, наперед заданного числа A меньше, чем на ε □ Предположим, что теорема неверна, а именно при заданном комплексном числе А и заданном ε>0 найдется |f(z)-A|> ε при |z-z0|< Рассмотрим вспомогательную функцию
тогда согласно определению функции f(z)= Из последнего, Из утверждения теоремы следует, что при различных способах стремления к существовенно особой точке z0 можно получить различные предельные значения. Пример 9.Определить характер особой точки z0=0 функции Пример 10. Найти особые точки и определить их характер Определение 12.Точка z=∞ называется изолированной особой точкой функции f(z), если существует R>0, что в области |z|>R нет других особых точек кроме нее самой, при этом: а) z=∞ - устранимая особая точка, если разложение f(z) в ряд Лорана в окрестности этой точки, не содержит слагаемых с положительными степенями z: f(z)= б) z=∞ - полюс m-го, если разложение в ряд Лорана содержит m слагаемых с положительными степенями (z-z0). в) z=∞ - существенно особая точка, если разложение в ряд Лорана содержит бесконечное число слагаемых с положительными степенями (z-z0). Пример 11.Определить характер особой точки z а) для функции f(z)=ez= б) для функции f(z)= в) для функции f(z)=z2 Вычеты. Пусть функция f(z) аналитическая в некоторой проколотой окрестности точки z0. Эта точка либо правильная, либо изолированная особая точка однозначного характера и в этой проколотой окрестности f(z) можно разложить в ряд Лорана: f(z) = Определение 13.Вычетом функции f(z) точки z0 называется коэффициент с-1 в разложении функции f(z) в ряд Лорана в окрестности точки z0 и обозначается: с-1=res f(z0)). Из формулы коэффициентов ряда Лорана получаем, что вычет будет равен: с-1=res f(z0)= где
Пример 12.Вычислить Решение. Разложим подинтегральную функцию в ряд Лорана:
Откуда
Тогда
Из формулы (14) видно, что если z0 правильная точка, то получится интеграл от аналитической функции, которая по теореме Коши равна нулю, т.о. вычет res f(z0)≡0. Устранимая точка по определению не содержит слагаемых с отрицательными степенями, поэтому вычет в устранимой точке так же всегда равен нулю. Теорема16(вычисление вычета в полюсе). Пусть z0 полюс m-го порядка функции f(z), причем z0≠∞, тогда вычет в этой точке определяется формулой: resf(z0)= В простом полюсе res f(z0)= □ Пусть z0 простой полюс, тогда разложение в ряд Лорана в его окрестности имеет вид: f(z)= Умножив левую и правую части на (z-z0) получим: f(z)(z-z0)=c-1+c0(z-z0)+c1(z-z0)2+…+cn(z-z0)n+1+… переходя к пределу в левой и правой части z→z0 получим (17). Пусть полюс m-го порядка, тогда разложение в ряд Лорана имеет вид: f(z)= f(z)(z-z0)n=с-m+…+с1(z-z0)m-1+с0(z-z0)m+…+сn(z-z0)m+n+… продифференцируем последнее равенство (m-1) раз по z и, переходя к пределу в левой и правой части при z→z0, получим (16). ■ Следствия.1) Пусть f(z) в окрестности точки z0 допускает представление
тогда z0 –полюс m-го порядка и res f(z0)= 2) Пусть f(z) в окрестности точки z0 может быть представлена как отношение двух функций f(z)= □ Пусть f(z)= Перейдем к пределу в левой и правой части и получим res f(z0)= Определение 14.Вычетом res f(z) относительно точки z=∞ называется коэффициент с-1 в разложении f(z) в окрестности бесконечно удаленной точки: с-1=resf(z0)= где -замкнутый контур, вне которой f(z) не имеет других особых точек кроме z=∞. Теорема 17(основная теорема о вычетах). Пусть f(z) аналитическая в односвязной области D за исключением конечного числа изолированных особых точек однозначного характера z1…zn и С-контур, содержащий внутри себя все точки z1…zn и целиком лежащий в области D. Тогда справедлива формула:
□ Окружим точки z1…zn контурами Следствие.Если f(z) аналитическая на всей комплексной плоскости, за исключением конечного числа изолированных особых точек однозначного характера, то сумма всех вычетов, включая и точку z=∞ равна нулю. Это следует из равенства (18). Если его разделить на –resf(∞). ■ Пример 13.Вычислить интеграл.
Точки z1=i, z2=-i-простые полюсы. Точка z3=-3 не лежит в круге res f(i)= res f(-i)=
Поиск по сайту: |
 функция аналитическая, но не является аналитической внутри круга |z-z0|<r, где r как угодно мало.
функция аналитическая, но не является аналитической внутри круга |z-z0|<r, где r как угодно мало. Точка z=0 является особой.
Точка z=0 является особой. sin
sin  обращается в ноль, т.е. все точки zk=
обращается в ноль, т.е. все точки zk=  являются особыми и изолированным, потому что мы можем выделить окрестности этих точек, в которых функции f(z) является аналитической.
являются особыми и изолированным, потому что мы можем выделить окрестности этих точек, в которых функции f(z) является аналитической. 2+…+
2+…+  +… ;
+… ;

 .
. ; f(z)=
; f(z)= 
 .
. ;
; 
 2+…+
2+…+ 
 Cr: |z-z0|=r 0<r<R.
Cr: |z-z0|=r 0<r<R. |≤
|≤ 

 , тогда можно представить
, тогда можно представить

 =
= 



 , что для любой точки проколотой окрестности 0<|z-z0|<R f(z)≠0. Рассмотрим вспомогательную обратную функцию g(z)=
, что для любой точки проколотой окрестности 0<|z-z0|<R f(z)≠0. Рассмотрим вспомогательную обратную функцию g(z)=  . Т.к. для f(z) выполняется условие, |f(z)|→∞, то g(z)→0 и для функции g(z) точка z0 , согласно теоремы 13, является устранимой, а согласно замечанию к ней можно записать
. Т.к. для f(z) выполняется условие, |f(z)|→∞, то g(z)→0 и для функции g(z) точка z0 , согласно теоремы 13, является устранимой, а согласно замечанию к ней можно записать ,
, 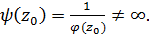
 аналитическая, поэтому из доказательства необходимости это означает, что z0 является полюсом m-го порядка, т.к.
аналитическая, поэтому из доказательства необходимости это означает, что z0 является полюсом m-го порядка, т.к.  ■
■ что во всех точках из
что во всех точках из  (z0
(z0  значение f(z) отличается от заданного числа А больше чем на ε, т.е.
значение f(z) отличается от заданного числа А больше чем на ε, т.е. (13)
(13) . В силу условия (13) функция f(z) определена и ограничена в Oδ(z0
. В силу условия (13) функция f(z) определена и ограничена в Oδ(z0  . Согласно теоремы 13, точка z0 для функции
. Согласно теоремы 13, точка z0 для функции 
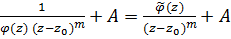 ;
;  .
. ограниченная в окрестности точки z0, полученное представление f(z) означает, что z0 является полюсом m-го порядка или правильной точкой при m=0, что противоречит условию теоремы. ■
ограниченная в окрестности точки z0, полученное представление f(z) означает, что z0 является полюсом m-го порядка или правильной точкой при m=0, что противоречит условию теоремы. ■ .
. .
.
 .
. z=∞-устранимая особая точка.
z=∞-устранимая особая точка. z=∞ полюс второго порядка.
z=∞ полюс второго порядка.
 (14)
(14) любой замкнутый контур, целиком лежащий в области аналитичной функции f(z) и содержащий внутри себя только одну особую точку z0. Из формулы (14) получаем:
любой замкнутый контур, целиком лежащий в области аналитичной функции f(z) и содержащий внутри себя только одну особую точку z0. Из формулы (14) получаем: (15)
(15)

 .
. .
. }. (16)
}. (16) f(z)(z-z0). (17)
f(z)(z-z0). (17)

 =
=  |
|  |<∞,
|<∞, .
. , тогда z0 простой полюс, причем вычет res f(z0)=
, тогда z0 простой полюс, причем вычет res f(z0)= 
 или f(z)(z-z0)=
или f(z)(z-z0)=  =
=  .
. =
=  .
.
 не пересекающиеся между собой и с контуром С. По теореме Коши для многосвязанной области имеем:
не пересекающиеся между собой и с контуром С. По теореме Коши для многосвязанной области имеем: 
 , тогда слева получится
, тогда слева получится
 формуле для вычисления вычета в простом полюсе, имеем
формуле для вычисления вычета в простом полюсе, имеем
 .
. =2𝜋i(
=2𝜋i( 