 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Числовые и функциональные рядыСтр 1 из 3Следующая ⇒
ГЛАВА 3. РЯДЫ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. ВЫЧЕТЫ. Рассмотрим бесконечную последовательность комплексных чисел
Частичные суммы образуют последовательность: s1=z1, s2= Определение 1.Формально составленная бесконечная сумма членов последовательности {zk} называется числовым рядом комплексных чисел и обозначается z1+z2+…+zn+….= Определение 2. Числовой ряд (1) называется сходящимся, если существует конечный предел последовательности его частичных сумм В терминах ε-N: Если s сумма ряда, то s= Здесь rn называется остатком ряда. Теорема 1.Числовой ряд с комплексными членами (1) сходится тогда и только тогда, когда сходятся ряды, составленные отдельно для действительной и мнимой частей □ Обозначим частичные суммы через sn=z1+z2+…+zn; тогда sn=z1+z2+..+zn=(x1+iy1)+(x2+iy2)+..+(xn+iyn)=(x1+x2+…+xn)+i(y1+y2+…+yn)=
По доказанной ранее теореме предел существует, если существуют пределы действительной и мнимой частей, т.е. Для рядов с комплексными членами имеет место следующая теорема, аналогичная теореме с действительными членами. Теорема 2.(Критерий Коши1789-1857) Числовой ряд (1) сходится тогда и только тогда, когда
Следствие(необходимый признак сходимости).Для того, чтобы числовой ряд (1) сходился необходимо и достаточно, чтобы предел его n-го члена равнялся нулю, т.е.
Определение 3.Числовой ряд (1) называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин Теорема 3.Ряд с комплексными членами (1) сходится, если сходится ряд составленный из абсолютных величин исходного ряда. □Пусть ряд Пример 1. Исследовать на сходимость ряд zn= По признаку Коши, т.к. Пусть в некоторой области D комплексной плоскости определены функции fn(z). Бесконечный набор {fn(z)}∞n=1 таких функций назовем функциональной последовательностью, а ряд, составленный из членов этой функциональной последовательности, назовем функциональным рядом: f1(z)+f2(z)+…+fn(z)+…= В каждой точке Определение 4. Функциональный ряд называется сходящимся в области D к функции f(z), если он сходится во всех точках области D причем суммой ряда является функция f(z): f(z)= На языке ε-N Кроме такой поточечной сходимости, есть понятие другой, равномерной сходимости. Определение 5.Функциональный ряд называется равномерно сходящимся в области D функции f(z), если
Теорема 4.(признак Вейерштрасса, 1815-1897гг.)Если всюду области D члены функционального ряда могут быть мажорированы членами абсолютно сходящегося числового ряда, то ряд (2) сходится в D равномерно, т.е. если
Пример 2. Показать, что в полуплоскости Решение. Для
Числовой ряд Замечание.Условие мажорируемости ряда (2) является достаточным для равномерной сходимости функционального ряда, однако оно не является необходимым. Теорема 5.(критерий Коши равномерной сходимости функционального ряда) Для того, чтобы функциональный ряд (2) равномерно сходился в области D необходимо и достаточно, чтобы
или
□ Доказательство аналогичное доказательству аналогичной теоремы для функциональных рядов действительных чисел. В теории рядов и в их применении важную роль играют следующие свойства равномерно сходящихся рядов. Теорема 6. Пусть функция a) f(z)= б) Если L кусочно-гладкая кривая, целиком лежащая в D, то функциональный ряд (2) можно почленно интегрировать, т.е
Доказательство аналогичное доказательству аналогичной теоремы для функциональных рядов действительных чисел. Теорема 7 (первая теорема Вейерштрасса ). Пусть члены функционального ряда f1(z), f2(z)…fn(z)… являются аналитическими в области D функции, а функциональный ряд а) сумма ряда f(z) является аналитической в D функцией; б) функциональный ряд можно почленно дифференцировать любое число раз, т.е. имеет место равенство в) функциональный ряд □ а) Рассмотрим любой замкнутый контур С, лежащий в области D и интеграл по этому контуру. По теореме 7 будем иметь
Рис. 1. б) Пусть z0 ∊D и С замкнутый контур такой, что z0 ∊DС. Обозначим через d=
Ясно, что
сходится равномерно на C и в силу теоремы 7 его можно почленно интегрировать. Умножим интегралы на m!/2πi, получим
Все интегралы являются интегралами Коши, т.е. имеем равенство f(m)( а, т.к. точка z0 и контур C выбраны произвольно, то утверждение б) доказано. в) Рассмотрим произвольную подобласть
Рис. 2.
Проведем еще один контур
Здесь
Обозначим через l длину контура С1 , и из (4) выводим неравенства
Это неравенство выполняется для всех n>N(ε)=N(ε1) и для всех z из замкнутой области Теорема 8. (вторая теорема Вейерштрасса)Пусть функции fn аналитические в области D и непрерывны в замыкании □ Рассмотрим разность частичных сумм ряда sn+m(z)--sn(z)=fn+1(z)+fn+2(z)+…+fn+m(z). Эта сумма аналитическая в D. Из равномерной сходимости ряда на границе области по критерию Коши следует, что |sn+m(z)-sn(z)|=|fn+1(z)+fn+2(z)+…+fn+m(z)|<ε Согласно принципу max модуля аналитической функции max значение модуля достигается на границе, иначе функция const. Тогда, из последнего неравенства, записанного для граничной точки, тем более будем иметь
Последнее, по критерию Коши, означает равномерную сходимость во всех внутренних точках области D.
Поиск по сайту: |
 Сумма первых n слагаемых такой последовательности называется n-ой частичной суммой:
Сумма первых n слагаемых такой последовательности называется n-ой частичной суммой:

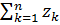 (1)
(1) =s≠∞. Этот предел называется суммой ряда.
=s≠∞. Этот предел называется суммой ряда. ,
,  n>N: |sn-s|<
n>N: |sn-s|<  .
.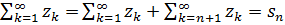 +rn,.
+rn,. и
и 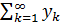
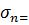 x1+x2+…+xn;
x1+x2+…+xn; 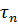 =y1+y2+…+yn,
=y1+y2+…+yn, 

 ,
,  ■
■ |<
|< 
 =0.
=0.
 сходится. Так как |
сходится. Так как |  => |zk |
=> |zk |  |xk|
|xk|  xk и |zk|
xk и |zk| 
 для действительных и мнимых частей, а это, по теореме 1, означает, что ряд с комплексными членами сходится. ■
для действительных и мнимых частей, а это, по теореме 1, означает, что ряд с комплексными членами сходится. ■ .
.  ; |zn|=|
; |zn|=|  |=
|=  =
= 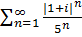 =
=  .
. =
= 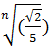 n=
n=  <1 ряд сходится, причем абсолютно.
<1 ряд сходится, причем абсолютно.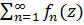 . (2)
. (2) будем иметь числовой ряд:
будем иметь числовой ряд:  .
.
 .
. (
( 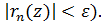
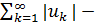 сходится и |fk(z)|
сходится и |fk(z)|  |uk|
|uk|  , то ряд
, то ряд  - сходится равномерно.
- сходится равномерно. По условию теоремы справедлива оценка |fk(z)|
По условию теоремы справедлива оценка |fk(z)|  Т.к. ряд
Т.к. ряд  сходится, то
сходится, то  , в силу оценки для членов ряда имеем, что |
, в силу оценки для членов ряда имеем, что |  . Т.е. остаток ряда |rn(z)|<ε, а это означает по определению (5) равномерную сходимость ряда (2) в области D. ■
. Т.е. остаток ряда |rn(z)|<ε, а это означает по определению (5) равномерную сходимость ряда (2) в области D. ■ ряд
ряд  сходится равномерно.
сходится равномерно.
 сходится, поэтому исходный функциональный ряд сходится равномерно в заданной области.
сходится, поэтому исходный функциональный ряд сходится равномерно в заданной области.
 .
. непрерывны в области D, а функциональный ряд
непрерывны в области D, а функциональный ряд  равномерно сходится к функции f(z) в D, тогда:
равномерно сходится к функции f(z) в D, тогда: является непрерывной в области D функцией.
является непрерывной в области D функцией.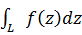 =
=  =
= 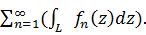
 тогда:
тогда: (z)=
(z)=  m)=
m)=  (3)
(3) сходится равномерно в любой замкнутой подобласти
сходится равномерно в любой замкнутой подобласти 
 т.к. все функции fn(z,) по условию, аналитические в D и по теореме Коши все интегралы правой части будут равны нулю, значит будет равен нулю интеграл и в левой части. Поскольку f(z) непрерывная в области D функция, а контур C произвольный, то по теореме Морера f(z) будет аналитический функцией в области D.
т.к. все функции fn(z,) по условию, аналитические в D и по теореме Коши все интегралы правой части будут равны нулю, значит будет равен нулю интеграл и в левой части. Поскольку f(z) непрерывная в области D функция, а контур C произвольный, то по теореме Морера f(z) будет аналитический функцией в области D.
 . Рассмотрим функцию
. Рассмотрим функцию .
. . Применяя критерий Коши, можно показать, что функциональный ряд
. Применяя критерий Коши, можно показать, что функциональный ряд =
= 


 и контур C , охватывающий подобласть, причем так, что расстояние z
и контур C , охватывающий подобласть, причем так, что расстояние z 
 =d>0
=d>0
 , охватывающий контур С, такой, что расстояние между ними не меньше, чем
, охватывающий контур С, такой, что расстояние между ними не меньше, чем  Остаток rn(z) ряда (2) является аналитической функцией в D, то для любой точки z
Остаток rn(z) ряда (2) является аналитической функцией в D, то для любой точки z  можно записать
можно записать dς. (4)
dς. (4) остаток ряда (3). Из равномерной сходимости ряда (2) на С1 следует, что
остаток ряда (3). Из равномерной сходимости ряда (2) на С1 следует, что .
. ∙
∙  .
.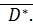 Поскольку z и
Поскольку z и 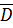 , причем ряд
, причем ряд 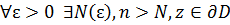
 .
.