 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Як вираховують динамічні напруження через статичні ⇐ ПредыдущаяСтр 2 из 2
де Вираз для динамічного коефіцієнта (12.6) можна записати в іншому вигляді, якщо скористатися залежністю між висотою
39.Визначення Кд при раптовому прикладанні навантаження Якщо h=0 (раптове прикладання вантажу), то Кд=2. Коли навантаження прикладається раптово ( Якщо вантаж падає з великої висоти
Класифікація коливань Механічні коливання діляться на чотири типи: власні або вільні, змушені, параметричні і автоколивання. Власними або вільними називаються коливання, які відбуваються під дією пружних сил самої системи. Прикладом може бути коливання вантажу закріпленого на пружині (рис. 10.2,а). Власні коливання будуть затухаючими, тому що існують сили опору. Змушениминазиваються коливання, що відбуваються під дією періодично змінної збурюючої сили. Змушеним коливанням піддається балка, на якій установлено електродвигун з незрівноваженими масами, що обертаються. Параметричними називають коливання пружної системи-в результаті зміни фізичних параметрів системи. Прикладом параметричних коливань будуть коливання стержня еліптичного перерізу при обертанні. Змінними фізичними параметрами будуть моменти інерції еліпса. Автоколиваннями називаються незатухаючі коливання елементів машин під дією зовнішніх сил, які знаходяться поза пружною системою. Прикладом автоколивань (самоколивань) буде коливання крила літака в повітряному потоці. 41.Визначення частоти вільних коливань з 1-м ступенем вільності
42.Означення числа ступенів вільності Число незалежних параметрів, які повністю визначають систему в просторі називають ступенем вільності системи. 43.Коефіцієнт наростання коливань (вимушені коливання) Амплітуда С змушених коливань, залежить від частоти цих коливань p. Відношення амплітуди С до амплітуди статичної деформації визначає так званий коефіцієнт наростання коливань β:
β = Як зазначилося, при розрахунках амплітуд змушених коливань зручно користуватися коефіцієнтом наростання амплітуди коливань β, що становить відношення амплітуди
44.Поняття про резонанс і шляхи його усунення У певних умовах коли частота збуджувальних сил близька до частоти власних коливань розглядуваної системи або збігається з нею, вимушені коливання супроводжуються значним (часто небезпечним) збільшенням амплітуди, що спричинює недопустимі для конструкції деформації (напруження) Це явище, як відомо має назву резонансу. Явище резонансу, що може виникнути при вимушених коливаннях, завжди небезпечне для конструкції. Різке зростання амплітуди коливань може призвести до недопустимо великих •переміщень у пружній системі і навіть до її руйнування. Тому при розрахунках систем, що зазнають коливань під дією періодично-змінних навантажень, основною задачею є забезпечення можливо великої різниці між частотами власних і вимушених коливань, тобто забезпечення так званої відстройки від резонансу. Оскільки частота власних коливань залежить лише від жорсткості системи, то перевірка на небезпеку резонансу є по суті розрахунком системи на жорсткість. При конструюванні елементів машин часто ставиться вимога, щоби частота вимушених коливань відрізнялася не менше як на 30% від частоти власних коливань системи. Важливе значення при проектуванні валів має визначення так званого критичного числа обертів вала. Внаслідок неминучих невеликих ексцентриситетів відносно осі вала розміщених на ньому різних деталей (шківів, «маховиків тощо) при обертовому русі вала виникають сили інерції з частотою со, яка дорівнює кутовій швидкості обертання вала. Ці сили діють на вал так, як збурюючі сили при вимушених коливаннях, і коли кутова швидкість обертання вала стає рівною коловій частоті соо його власних поперечних або крутильних коливань, настає явище резонансу, вал починає хитатися. Таким чином, критична кутова швидкість соКр обертового руху вала визначається з умови 45.Означення оболонки Оболонка – тіло, обмежене двома криволінійними поверхнями, відстань між якими мала у порівнянні з іншими розмірами (рис.1.2,б).
Нагадаємо, що оболонкою називають тіло, яке обмежене двома криволінійними поверхнями, відстань між якими – товщина оболонки Поверхня, яка поділяє товщину Тонкостінними називають такі оболонки, для яких відношення товщини до найменшого радіуса кривини поверхні
Якщо серединна поверхня оболонки отримана у результаті обертання кривої відносно деякої осі, то така оболонка називається оболонкою обертання. Оболонки обертання ще називають осесиметричними. До таких оболонок відносять циліндричні, конічні, сферичні, а також еліпсоїди, параболоїди тощо. 46.Як познакчаються Мередіальні і поперечні (широтні) напруження ??
Ϭt
47.Що таке безмоментна теорія оболонок ?? Модель тонкостінної оболонки базується на гіпотезах Кірхгофа–Лява: - прямолінійний елемент, що є перпендикулярним до серединної поверхні, після деформації залишається прямолінійним і нормальним до серединної поверхні, а його довжина не змінюється; - нормальними напруженнями на площадках, що паралельні до серединної поверхні, можна знехтувати. Задачу про розрахунок осесиметричної тонкостінної оболонки вирішити найбільш просто, якщо припустити, що напруження розподіляються по товщині оболонки рівномірно, тобто згин оболонки відсутній. Теорію оболонок, що базується на цьому припущенні називають безмоментною. Для застосування цієї теорії необхідне виконання ряду умов: - оболонка повинна мати плавні контури (без різких змін кривин чи товщини); - граничні умови повинні бути такими, щоб реакції зводилися до сил, що діють в серединній поверхні; - навантаження повинно плавно розподілятись по поверхні оболонки. З погляду раціонального використання матеріалу конструкції безмоментний напружений стан є вигідним. Тому при конструюванні слід прагнути до створення умов при яких можна реалізувати безмоментний напружений стан. 48.Рівняння Лапласса ??
Ϭt - широтні (колові) нормальні напруження.
Поиск по сайту: |
 ,
,
 - напруження, що виникає при статичному прикладанні навантаження.
- напруження, що виникає при статичному прикладанні навантаження. та швидкістю
та швидкістю  у момент зіткнення. Знаючи, що
у момент зіткнення. Знаючи, що  , звідки
, звідки  , матимемо
, матимемо .
.
 ,
,  ), то
), то  , а
, а 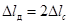 ;
;  .
. , то вираз для динамічного коефіцієнта спрощується:
, то вираз для динамічного коефіцієнта спрощується: .
.

 - статичне переміщення балки від сили F=1 H в точці коливання мас.
- статичне переміщення балки від сили F=1 H в точці коливання мас.

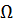 змушених коливань до статичного переміщення
змушених коливань до статичного переміщення 


 , мала порівняно з іншими розмірами тіла. Ми будемо розглядати оболонки сталої товщини (
, мала порівняно з іншими розмірами тіла. Ми будемо розглядати оболонки сталої товщини (  ).
). є меншим, ніж 1/20, тобто
є меншим, ніж 1/20, тобто .
.
 Мередіальні напруження позначаються – Ϭм і ρм,а широтні (колові) напруження – Ϭt і ρt. Якщо ці всі дані підставити в рівняння,отримаємо формулу Лапласса. Ϭt
Мередіальні напруження позначаються – Ϭм і ρм,а широтні (колові) напруження – Ϭt і ρt. Якщо ці всі дані підставити в рівняння,отримаємо формулу Лапласса. Ϭt




 ϬмϬм
ϬмϬм