 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Якщо перетин балки має тільки одну вісь симетрії в площині навантаження, то в граничному стані нейтральна вісь не пройде через центр ваги поперечного перерізу ⇐ ПредыдущаяСтр 3 из 3
Положення нейтральної осі визначається з рівності нулю суми проекцій на вісь балки всіх сил
де
25. Як змінюються нормальні напруження по висоті балки?
Максимальні нормальні напруження знаходять за формулою:
де На рис. 6.8 показано епюри напружень
Аналіз залежності (6.8) показує, що нормальні напруження в поперечному перерізі: - по ширині перерізу розподілені рівномірно; - по висоті перерізу змінюються за лінійним законом; - при найбільших значень досягають в точках найбільш віддалених від нейтральної осі
26. Жорсткість поперечного перерізу при згині? Добуток Під розрахунком на жорсткість ми розуміємо оцінку пружної податливості балки під дією прикладених навантажень і підбір таких розмірів поперечного перерізу, при яких переміщення не будуть перевищувати установлених нормами границь.
27. Як визначити дотичні напруження в поперечному перерізі балки? При виведенні формули для дотичних напружень користуються певними допущеннями, які дають можливість одержати цю формулу за допомогою нескладних методів опору матеріалів. Російський вчений Д.І. Журавський показав, що дотичні напруження досягають порівняно великих значень у перерізах, що мають форму вузьких і високих прямокутників, та у перерізах, які можна розкласти на такі прямокутники. Для таких перерізів можна прийняти дві гіпотези: Q(x) – поперечна сила в перерізі балки;
28. Сформулюйте умову міцності балок за нормальними напруженнями Умова міцності при чистому плоскому згинанні maxτz= max Mx/Wx≤[τ], де max Mx – згинальний момент у небезпечному перерізі; Wx = (Ix /ymax) – осьовий момент опору цього перерізу; Ix – момент інерції цього перерізу відносно його нейтральної лінії; ymax – найбільше віддалення від нейтральної осі до крайніх точок перерізу; [τ ] – допустиме нормальне напруження. Максимальне значення згинального момента береться з епюри Мx.
30Яких переміщень зазнають поперечні перерізи балки при прямому згині?? Зігнута вісь балки при прямому згині є плоскою кривою, що лежить в одній з головних площин балки. Її називають також пружною лінією балки. Переміщення центру ваги перерізу в напрямку, перпендикулярному до осі балки, називають прогином балки в даній точці (перерізі) - Кут, на який переріз балки повертається відносно свого початкового положення, називають кутом повороту перерізу -
Рисунок 6.15 а, б
31Диференціальне рівняння зігнутої осі балки?? Переміщення центру ваги перерізу в напрямку, перпендикулярному до осі балки, називають прогином балки в даній точці (перерізі) - Кут, на який переріз балки повертається відносно свого початкового положення, називають кутом повороту перерізу - При малих деформаціях горизонтальними складовими переміщень нехтують. На рис. 6.15
Для визначення деформацій балки скористаємось виразом закону Гука при згині
Тепер встановимо зв’язок між кривиною
звідси
враховуючи малість деформацій
Прирівнюючи праві частини (6.31) і (6.32), одержимо наближене диференціальне рівняння зігнутої осі балки
32 Запишіть загальні інтеграли рівняння зігнутої осі баки. Як визначають сталі інтегрування? Необхідні диференціальні залежності для Мі Q в будь–якому перерізі запишемо так:
проінтегрувавши рівняння (6.33) один раз отримаємо рівняння кутів поворотів
Інтегруючи другий раз, отримуємо рівняння прогинів
де
Поиск по сайту: |
 , розподілених по її перетину:
, розподілених по її перетину:
 — площа розтягнутої зони перетину;
— площа розтягнутої зони перетину; — площа стиснутої зони.
— площа стиснутої зони.
 ,
,
 - осьовий момент опору перерізу відносно нейтральної осі.
- осьовий момент опору перерізу відносно нейтральної осі.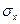 у випадку симетричного (рис. 6.8,а) відносно нейтральної осі поперечного перерізу балки.
у випадку симетричного (рис. 6.8,а) відносно нейтральної осі поперечного перерізу балки. 
 , тобто на осі
, тобто на осі  , дорівнюють нулеві;
, дорівнюють нулеві; називають жорсткістю поперечного перерізу балки при згині
називають жорсткістю поперечного перерізу балки при згині у вузьких перерізах мають по всій ширині перерізу вертикальний напрямок і рівнодійна їх, що діє в напрямку осі y, – це поперечна сила Q(x);
у вузьких перерізах мають по всій ширині перерізу вертикальний напрямок і рівнодійна їх, що діє в напрямку осі y, – це поперечна сила Q(x); , (7.18) де (рис. 7.14, а):
, (7.18) де (рис. 7.14, а):

 – статичний момент відсіченої площі відносно осі z;
– статичний момент відсіченої площі відносно осі z; – відсічена площа (заштрихована на рисунку площа, що лежить по один бік від точки, в якій визначають напруження);
– відсічена площа (заштрихована на рисунку площа, що лежить по один бік від точки, в якій визначають напруження);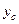 – координата центра відсіченої площі.
– координата центра відсіченої площі.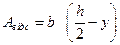 ;
; ;
; ;
; .
. .
. .
. .
.



 та
та  - прогин та кут повороту перерізу в точці
- прогин та кут повороту перерізу в точці  . Використовуючи геометричний зміст першої похідної функції
. Використовуючи геометричний зміст першої похідної функції  ,
,
 .
.
 .
.
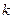 і прогином
і прогином  , що лежать на відстані
, що лежать на відстані  одна від одної (рис. 6.16). Дотична до лінії прогинів в точці
одна від одної (рис. 6.16). Дотична до лінії прогинів в точці  з горизонталлю. В точці
з горизонталлю. В точці  , причому
, причому  є кутом між нормалями
є кутом між нормалями  і
і  . Виразимо довжину дуги через центральний кут
. Виразимо довжину дуги через центральний кут ,
,
 ,
,
 та вираз (6.30), одержимо
та вираз (6.30), одержимо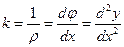 .
.
 (6.33)
(6.33) ;
;  . (6.33)
. (6.33) і
і  - сталі інтегрування, що визначаються із крайових умов балки і граничних умов її ділянок.
- сталі інтегрування, що визначаються із крайових умов балки і граничних умов її ділянок.