 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Що називають одиничним станом пружної системи?Стр 1 из 2Следующая ⇒
ЗАГАЛЬНІ МЕТОДИ ВИЗНАЧЕННЯ ПЕРЕМІЩЕНЬ
Що таке узагальнена сила і узагальнене переміщення? Робота сили, що статично діє на довільну пружну систему Тут під силою
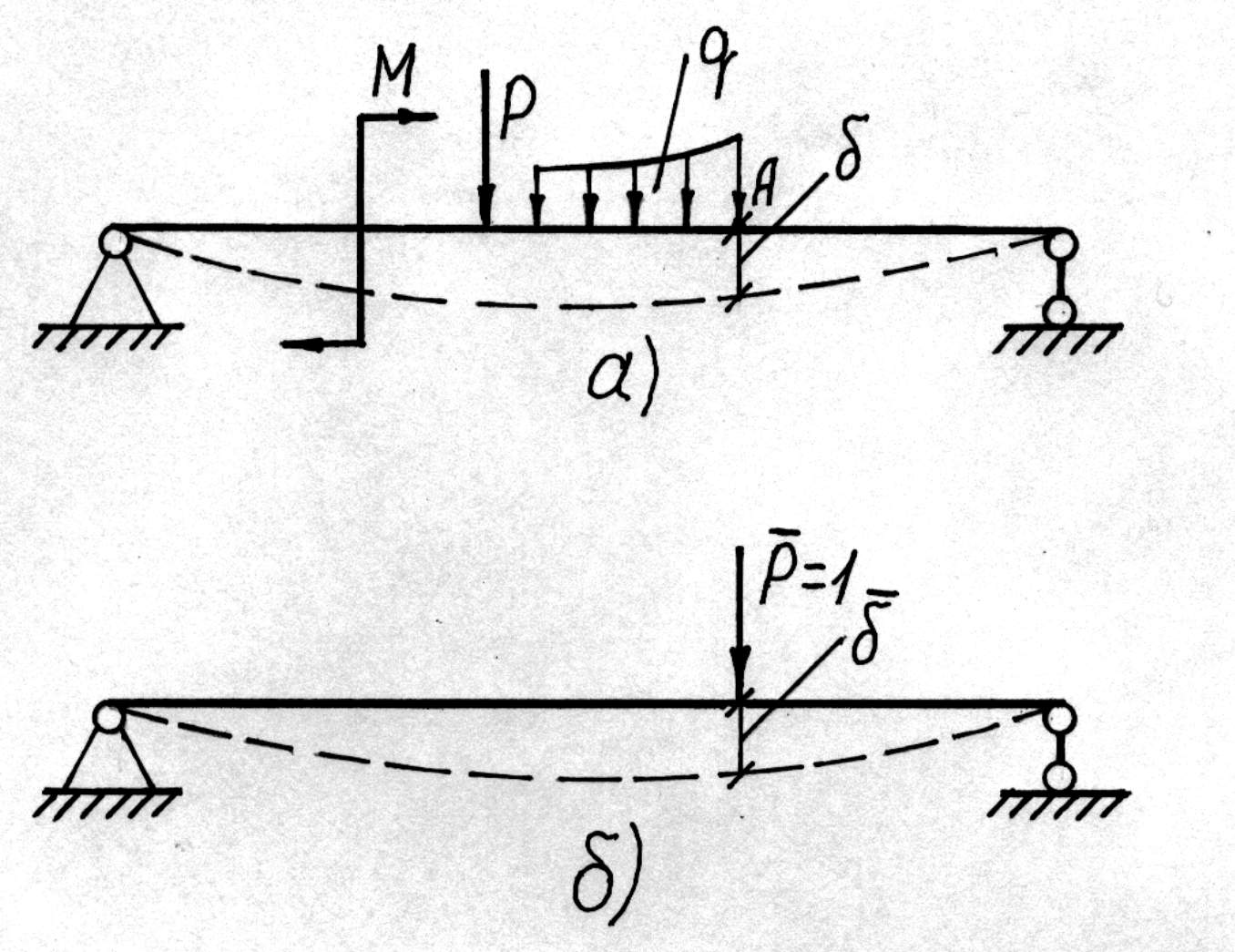
2. Що таке грузова епюра? Розглянемо прямий поперечний згин балки, що навантажена довільним зовнішнім навантаженням (рис. 7.4,а). Такий стан балки назвемо грузовим.
Що називають одиничним станом пружної системи? Знайдемо прогин точки
5. Запишіть інтеграл Мора для прямого поперечного згину. формулу Мора (інтеграл Мора) для прямого поперечного згину
Тут
6. Який порядок визначення лінійних та кутових переміщень з допомогою інтеграла Мора? При визначенні переміщень дотримуються такої послідовності дій: 1) Будують епюри внутрішніх силових факторів від заданого навантаження (грузові епюри); 2) Відкинувши задане навантаження, в перерізі, де визначають переміщення, прикладають одиничну силу (або момент) у напрямку шуканого переміщення і будують епюри внутрішніх силових факторів (одиничні епюри); 3) „Перемножують” грузові епюри з одиничними за формулою
7. Обчислення інтеграла Мора за способом Верещагіна.
8. тут чисельник кожного доданка дорівнює добутку площі
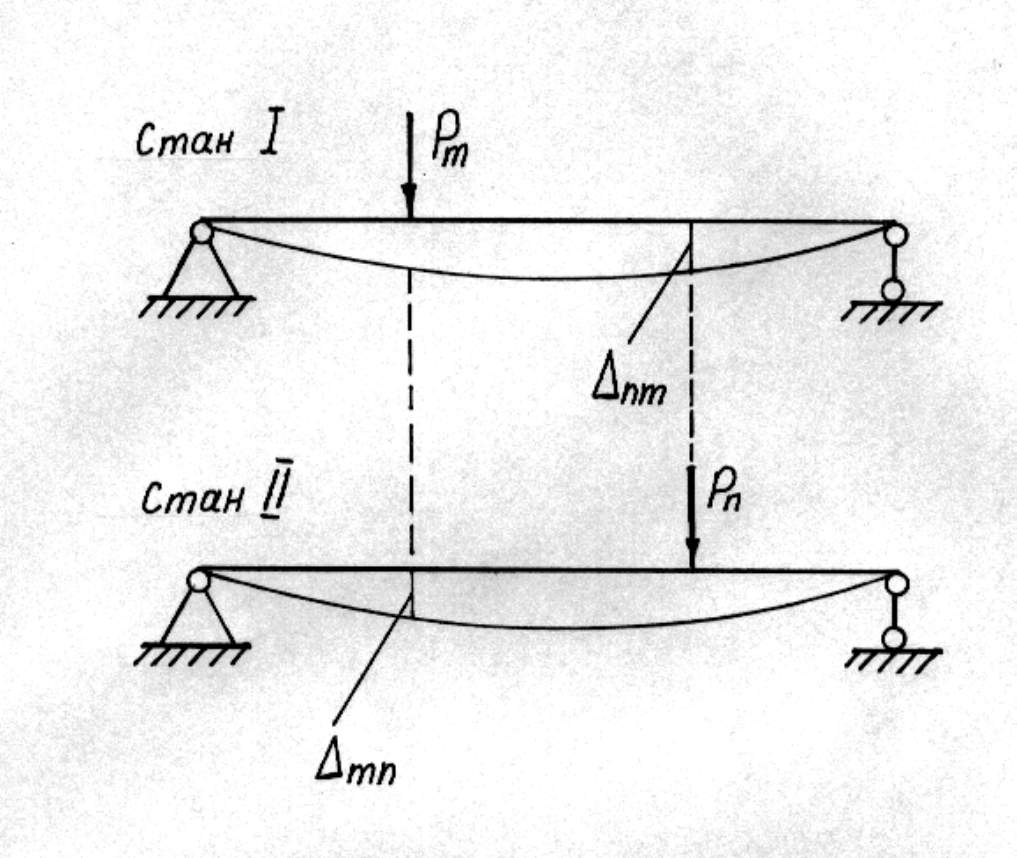
9. Теорема про взаємність робіт (теорема Бетті). Можлива робота сил першого стану на переміщеннях в їх напрямку, що викликані силами другого стану, дорівнює можливій роботі сил другого стану на переміщеннях в їх напрямку, але викликаних силами першого стану (рис. 7.2)
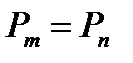 , то , то
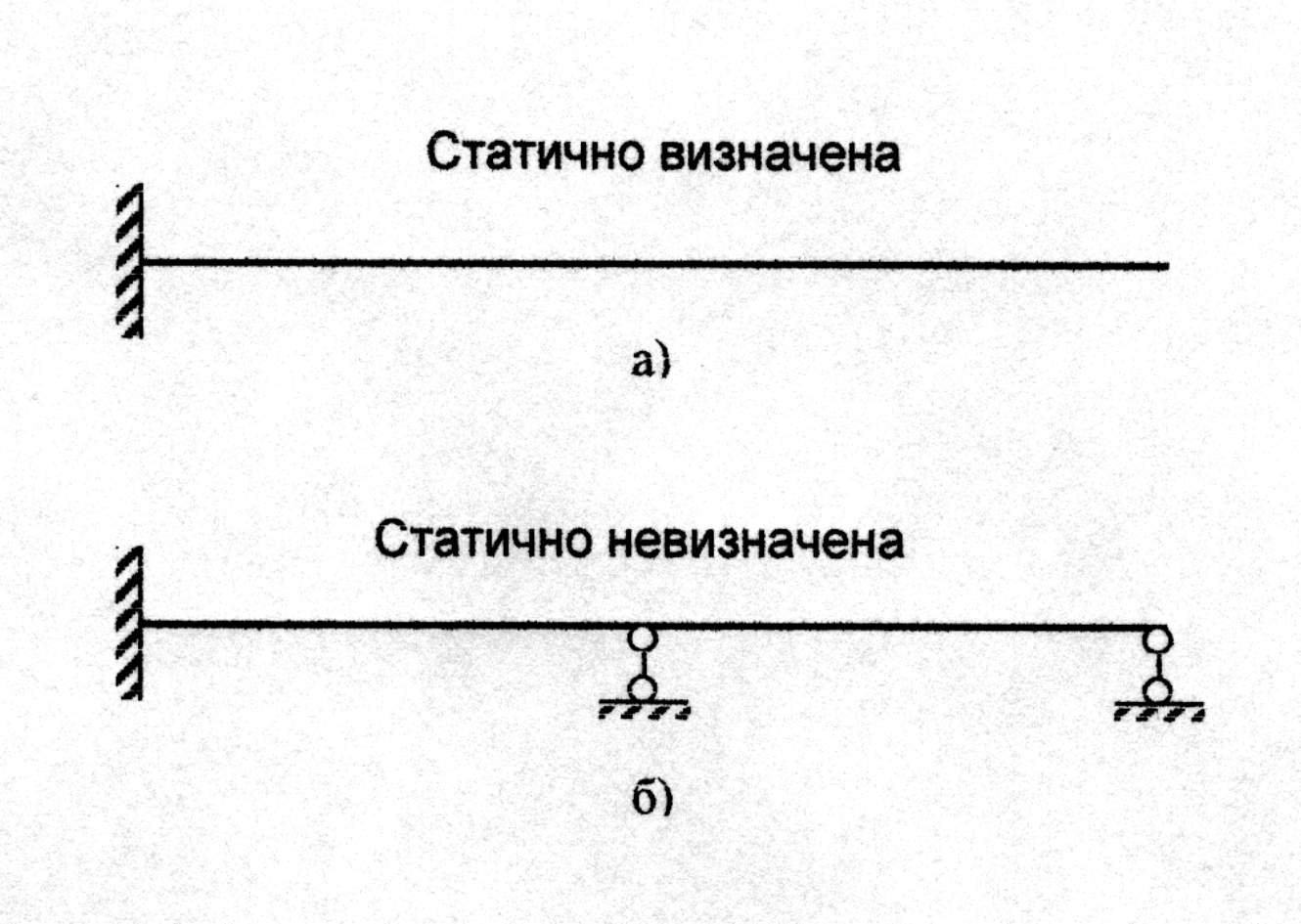
Статично невизначена балка 1. Які балки називають статично невизначеними? Якщо кількість реакцій, що виникають у накладених на балку в’язах перевищує кількість рівнянь статики, які можна скласти, то балку називають статично невизначеною.
2. Що називають ступенем статичної невизначеності балки? Ступінь статичної невизначеності
де
3. 4. 5. Метод сил - це найбільш загальний метод розкриття статичної невизначеності стержнів, балок та стержневих систем (рам, арок, ферм тощо).
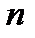 разів статично невизначену балку (рис. 8.3,а). Шляхом видалення разів статично невизначену балку (рис. 8.3,а). Шляхом видалення 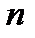 зайвих в’язей вихідну балку перетворюють у статично визначену (рис.8.3,б), яку називають основною системою методу сил. Вибрати зайвих в’язей вихідну балку перетворюють у статично визначену (рис.8.3,б), яку називають основною системою методу сил. Вибрати 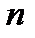 зайвих в’язей можна по різному, тобто для однієї балки можна утворити кілька основних систем (тут слід керуватися тим, щоб розрахунок у вибраному зайвих в’язей можна по різному, тобто для однієї балки можна утворити кілька основних систем (тут слід керуватися тим, щоб розрахунок у вибраному
Завантаживши основну систему зовнішнім навантаженням і невідомими реактивними силами Невідомі сили Використовуючи принцип суперпозиції, запишемо вирази для знаходження прогинів балки в точках кріплення видалених в’язей
Нагадаємо, що, наприклад, позначка
або загалом
6. Запишіть систему канонічних рівнянь.
Рівняння переміщень, що записані у вигляді (8.2), називають канонічними рівняннями методу сил (тут пунктиром виділені рівняння для один раз та два рази статично невизначених балок). Необхідна кількість рівнянь дорівнює ступеню статичної невизначеності балки. Переміщення Для визначення головних коефіцієнтів
Для визначення бічних коефіцієнтів канонічних рів- нянь множити з відповідними епюрами
Нагадаємо, що за теоремою про взаємність переміщень
Для визначення вільних членів канонічних рівнянь
8. Як визначаються коефіцієнти і вільні члени системи канонічних рівнянь? Для перевірки правильності визначення коефіцієнтів і вільних членів канонічних рівнянь необхідно побудувати сумарну одиничну епюру, додаючи із врахуванням знаків всі одиничні епюри.
При перемноженні за способом Верещагіна сумарної одиничної епюри
Така перевірка називається перевіркою за рядками. Крім перевірки за рядками, можлива універсальна перевірка. Згідно із нею сума всіх коефіцієнтів рівнянь повинна дорівнювати добутку (за Верещагіним) сумарної одиничної епюри
Для вільних членів канонічних рівнянь перевірка зводиться до наступного: їх сума повинна дорівнювати добутку сумарної епюри
Стійкість стиснутого стержня.
1. Форми пружної рівноваги. Коефіцієнт запасу стійкості. У стані стійкої рівноваги перебуває важка кулька на дні сферичного заглиблення (рис. 10.1,а). При відхиленні кульки від початкового положення вона після певної кількості коливань повернеться у вихідний стан. Стиснутий стержень перебуває в стані стійкої рівноваги, якщо стискаюча сила Кулька на горизонтальній плоскій поверхні (рис.10.1,б) перебуває в стані байдужої рівноваги, оскільки будь-яке її положення буде однаково стійким. Форма рівноваги стиснутого стержня є байдужою, коли стискаюча сила досягає критичного значення. При цьому стержень може зберегти
Кулька на опуклій поверхні (рис. 10.1,в) перебуває в стані нестійкої рівноваги. У разі виведення кульки з цього положення у вихідний стан вона не повернеться. Стиснутий стержень перебуває в стані нестійкої рівноваги, якщо стискаюча сила перевищує критичне значення. При цьому прямолінійна форма рівноваги стає нестійкою. Втрата стійкості – це відхилення осі стержня від прямолінійної форми рівноваги, спричинене дією стискаючої сили.
Для безпечної роботи стиснутих стержнів необхідно, щоб стискаюче навантаження було меншим за критичну силу:
де Величину коефіцієнта запасу стійкості приймають трохи більшою, ніж величину коефіцієнта запасу міцності, оскільки беруть до уваги додаткові несприятливі обставини: початкове викривлення стержня, ексцентриситет прикладання навантаження та ін. Для сталевих стержнів
2. Формула Ейлера для критичної сили. Пояснення.
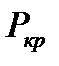 . Припускається, що напруження під дією критичної сили не перевищують границі пропорційності. У цьому разі стан рівноваги стержня буде байдужим, тобто викривлена форма стержня також буде зрівноваженою. Розглянемо стан стержня із зігнутою віссю, але вважатимемо відхилення від прямої форми неістотним. Тоді диференціальне рівняння осі стержня має вигляд . Припускається, що напруження під дією критичної сили не перевищують границі пропорційності. У цьому разі стан рівноваги стержня буде байдужим, тобто викривлена форма стержня також буде зрівноваженою. Розглянемо стан стержня із зігнутою віссю, але вважатимемо відхилення від прямої форми неістотним. Тоді диференціальне рівняння осі стержня має вигляд
де Введемо позначення
Загальний інтеграл цього рівняння є гармонічною функцією
Підставивши граничні умови в розв’язок (10.4), дістанемо систему двох рівнянь
Стала інтегрування
звідки
де У розрахунках на стійкість практичне значення має найменша критична сила, що відповідає рівності
Рівняння (10.8) називається формулою Ейлера. Якщо
Отже, якщо стискаюча сила Якщо
3. Межі застосування формули Ейлера. Що робити коли вони не виконуються. Оскільки формула Ейлера виведена в припущенні, що критичні напруження не перевищують границі пропорційності, існують певні межі її застосування, які визначаються нерівностю
де З нерівності (10.19) визначимо умову, яку повинна задовільняти гнучкість стержня, щоб формула Ейлера була застосовною:
Знак рівності в цій умові відповідає граничній гнучкості
тобто для сталі Ст3 формула Ейлера застосована при
де За формулою Ясинського обчислюють критичні напруження для стержнів середньої гнучкості, що широко використовуються в багатьох сталевих та залізобетонних конструкціях. Для сталевих (Ст3) стержнів середня гнучкість становить Прямо пропорційній залежності між критичним напруженням та гнучкістю для стержнів середньої гнучкості на графіку (див. рис. 10.6) відповідає похила пряма ділянка – так звана пряма Ясинського, що продовжує гіперболу Ейлера. Стержні малої гнучкості
4. Вплив способу закріплення на критичну силу.Зведена довжина. Розглянемо вплив першого фактору, тобто вплив умов закріплення стержня. Формулу (10.10) можна отримати, якщо розглянути рівняння поздовжнього згину четвертого порядку
Загальний інтеграл цього рівняння має вигляд
Сталі
Використовуючи ці умови, одержимо систему однорідних рівнянь
Система (10.15) матиме ненульове рішення, якщо її визначник дорівнює нулю:
Розкривши цей визначник, отримаємо трансцендентне рівняння для визначення
Найменший корінь цього рівняння визначає першу критичну силу
Таким чином
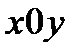 застосоване жорстке затиснення кінців стержня, тоді як у площині більшої жорсткості застосоване жорстке затиснення кінців стержня, тоді як у площині більшої жорсткості  - шарнірне. - шарнірне.
У таких випадках критичною силою для стержня буде менша з двох визначених окремо для кожної з головних площин:
де
де
Величину Коефіцієнти 1) характеру в’язей, що накладені на торцеві і проміжні перерізи стержня; 2) виду навантаження стержня зовнішніми силами (зосереджені чи розподілені) та місця їх прикладання; 3) характеру зміни перерізу стержня по його довжині.
5. Гнучкість стержня. Критичні напруження.
У стиснутому стержні критичні напруження виникають під дією критичної сили:
Урахувавши, що відношення
Введемо безрозмірну величину
Бачимо, що гнучкість стержня є його узагальненою геометричною характеристикою. Чим вона вища, тим гірше стержень опирається поздовжньому згину. Тепер критичне напруження визначатиметься за формулою
Залежність між критичним напруженням та гнучкістю можна подати у вигляді гіперболічної кривої – гіперболи Ейлера (рис. 10.6).
де З нерівності (10.19) визначимо умову, яку повинна задовільняти гнучкість стержня, щоб формула Ейлера була застосовною:
Знак рівності в цій умові відповідає граничній гнучкості
тобто для сталі Ст3 формула Ейлера застосована при
6.Формула ясинського для критичної сили. Поясніть як і коли її використовувати.
де За формулою Ясинського обчислюють критичні напруження для стержнів середньої гнучкості, що широко використовуються в багатьох сталевих та залізобетонних конструкціях. Для сталевих (Ст3) стержнів середня гнучкість становить Прямо пропорційній залежності між критичним напруженням та гнучкістю для стержнів середньої гнучкості на графіку (див. рис. 10.6) відповідає похила пряма ділянка – так звана пряма Ясинського, що продовжує гіперболу Ейлера. Стержні малої гнучкості
7. Класифікація стержнів за гнучкістю. Графік залежності критичних напр. Введемо безрозмірну величину
Бачимо, що гнучкість стержня є його узагальненою геометричною характеристикою. Чим вона вища, тим гірше стержень опирається поздовжньому згину. Тепер критичне напруження визначатиметься за формулою
Залежність між критичним напруженням та гнучкістю можна подати у вигляді гіперболічної кривої – гіперболи Ейлера (рис. 10.6). Оскільки формула Ейлера виведена в припущенні, що критичні напруження не перевищують границі пропорційності, існують певні межі її застосування, які визначаються нерівностю
де З нерівності (10.19) визначимо умову, яку повинна задовільняти гнучкість стержня, щоб формула Ейлера була застосовною:
Знак рівності в цій умові відповідає граничній гнучкості
тобто для сталі Ст3 формула Ейлера застосована при
де За формулою Ясинського обчислюють критичні напруження для стержнів середньої гнучкості, що широко використовуються в багатьох сталевих та залізобетонних конструкціях. Для сталевих (Ст3) стержнів середня гнучкість становить Прямо пропорційній залежності між критичним напруженням та гнучкістю для стержнів середньої гнучкості на графіку (див. рис. 10.6) відповідає похила пряма ділянка – так звана пряма Ясинського, що продовжує гіперболу Ейлера. Стержні малої гнучкості
8. Умова стійкості. Коеф. зменшення допустимого напруження (розкрити зміст). У розрахунках на стійкість критичне напруження є руйнівним, як границя текучості або границя міцності в розрахунках на міцність. Тому введено поняття допустимого напруження на стійкість
де Умова стійкості вимагає, щоб напруження, яке виникає при стисканні, не перевищувало допустимого напруження на стійкість:
Проте обчислення допустимого напруження на стійкість ускладнюється внаслідок того, що критичне напруження залежить не лише від властивостей матеріалу, а й від гнучкості стержня. Знайдемо залежність між допустимим напруженням на стійкість та допустимим напруженням на міцність при стиску:
де Шукана залежність
де Коефіцієнт Отже, з урахуванням залежності (10.23) умова стійкості набирає вигляду
9. Перевірний розрахунок на стійкість. Опишіть послідовність дій.
Перевірка стійкості полягає у перевірці виконання умови стійкості - визначають мінімальний момент інерції поперечного перерізу стержня та мінімальний радіус інерції (при однаковому закріпленні в головних площинах):
- обчислюють гнучкість стержня за формулою - за таблицями вибирають коефіцієнт зменшення основного допустимого напруження добуті вихідні дані підставляють в умову стійкості
10. Проектний розрахунок на стійкість. Опишіть послідовність дій. Добір поперечного перерізу стержня, або проектувальний розрахунок, здійснюється на підставі обчислення площі перерізу з умови стійкості:
Ця задача не має єдиного розв’язку, оскільки до нерівності (10.26) входять дві невідомі величини: площа перерізу - беруть довільне значення коефіцієнта
- відповідно до обчисленої площі визначають розміри перерізу або вибирають номер профілю із сортаменту; - визначають радіус інерції та гнучкість стержня, за якою з таблиць знаходять j1*; - порівнюють коефіцієнти j1 та j1* і, якщо розбіжність невелика, перевіряють умову стійкості (10.24); у разі істотної розбіжності значень j1 та j1* виконують друге наближення, для якого оптимальним значенням коефіцієнта зниження основного допустимого напруження j2 буде середньоарифметичне
Після цього повторюють всі зазначені дії. Щоб отримати задовільний розв’язок, здебільшого треба виконати кілька наближень.
Розрахунок на міцність та жорсткість при ударі.
1. Що таке ударне навантаження? Технічна теорія удару. Визначення прискорень частинок матеріалу при ударі досить проблематичне. Тому для розв’язання задач зазвичай використовують закон збереження енергії. При цьому будують спрощену розрахункову модель системи, що базується на кількох припущеннях, які в більшості випадків забезпечують достатній для інженерних розрахунків рівень точності. 1. Напруження, що виникають в системі при ударі, не перевищують границю пропорційності матеріалу, тобто завжди можна використовувати закон Гука. 2. Удар будемо вважати ідеально непружним (без відскакування). Тобто падаюча маса після удару наче прилипає до тіла, що зазнає удару, після чого вони продовжують рухатися разом. 3. Місцеві деформації, що виникають в місці контакту тіл не враховуємо. 4. Розглядаємо випадки, коли маса пружного тіла, що зазнає удару, мала порівняно з масою тіла, що удару завдає. Тому пружну систему вважаємо безмасовою. Разом з цим нехтуємо явищем розповсюдження хвиль деформацій. 5. Вважаємо, що кінетична енергія, падаючого тіла повністю перетворюється у потенціальну енергію пружної деформації тіла, яке сприймає удар. 6. Закон розподілу напружень і деформацій по об’єму тіла, яке зазнає удару, залишається таким самим як і при статичній дії сил. На основі цих припущень визначимо переміщення і напруження, що виникають в стержнях при ударі. Зазначимо, що в рамках технічної теорії удару можна врахувати вплив маси пружної системи. Це підвищує точність розрахунків.
2. Динамічний коефіцієнт при ударі. Позначивши динамічний коефіцієнт при поздовжньому ударі як
отримаємо
а враховуючи лінійний зв’язок між напруженнями і деформаціями
де Вираз для динамічного коефіцієнта (12.6) можна записати в іншому вигляді, якщо скористатися залежністю між висотою
Коли навантаження прикладається раптово ( Якщо вантаж падає з великої висоти
- динамічний коефіцієнт при поперечному ударі.
3. Напруження та переміщення при поздовжньому ударі. Нехай на стержень довжиною
а потенціальна енергія пружної деформації стержня
Використовуючи вираз закону Гука
Врахуємо, що абсолютне видовження стержня при статичному прикладанні вантажу (рис. 12.1,б)
тоді розділивши ліву і праву частини рівняння (12.4) на жорсткість стержня
Розв’язавши його відносно
В останній формулі слід остаточно прийняти знак плюс, оскільки знак мінус не відповідає фізичному змісту задачі (очевидно, що
4. Напруження та переміщення при поперечному ударі
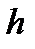 вільно падає вантаж вільно падає вантаж  (рис. 12.2,а). Розв’язуючи задачу так само, як і при поздовжньому уда-рі, прийдемо до рівняння (рис. 12.2,а). Розв’язуючи задачу так само, як і при поздовжньому уда-рі, прийдемо до рівняння
Вираз (12.11) однаковий для довільних умов на краях балки. Можуть змінюватися лише абсолютні значення Розв’язавши рівняння (12.11) відносно
де
Розрахунок на міцність при повторно змінних напруженнях.
Поиск по сайту: |
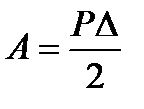
 будемо розуміти узагальнену силу - будь-який силовий вплив: зосереджену силу, групу сил, розподілене навантаження, зосереджений момент і т.п. Під переміщенням
будемо розуміти узагальнену силу - будь-який силовий вплив: зосереджену силу, групу сил, розподілене навантаження, зосереджений момент і т.п. Під переміщенням  будемо розуміти узагальнене переміщення - той вид переміщення, на якому узагальнена сила виконує роботу.
будемо розуміти узагальнене переміщення - той вид переміщення, на якому узагальнена сила виконує роботу.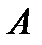 . Для цього розвантажимо балку, а в напрямку шуканого переміщення прикладемо оди-ничну (безрозмірну) силу
. Для цього розвантажимо балку, а в напрямку шуканого переміщення прикладемо оди-ничну (безрозмірну) силу 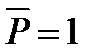 . Такий стан балки назвемо одиничним.
. Такий стан балки назвемо одиничним.
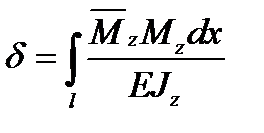 .
.
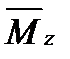 - вираз згинного моменту, що виникає в одиничному стані,
- вираз згинного моменту, що виникає в одиничному стані, 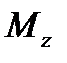 - вираз згинного моменту в грузовому стані.
- вираз згинного моменту в грузовому стані.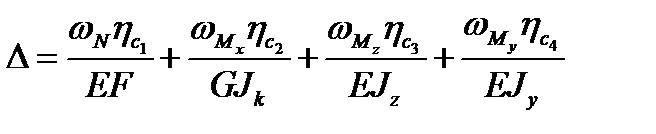
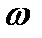 нелінійної епюри на ординату
нелінійної епюри на ординату 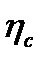 лінійної епюри, що відповідає центру ваги нелінійної. Добуток площі нелінійної епюри на ординату лінійної
лінійної епюри, що відповідає центру ваги нелінійної. Добуток площі нелінійної епюри на ординату лінійної 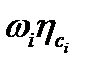 вважають додатнім, якщо площа і ордината розміщені з одного боку від осі епюри.
вважають додатнім, якщо площа і ордината розміщені з одного боку від осі епюри. . Ця теорема справедлива як для зовнішніх, так і для внутрішніх сил, тобто
. Ця теорема справедлива як для зовнішніх, так і для внутрішніх сил, тобто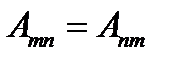 ;
; 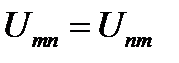 ;
;  .
.
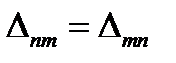 . (7.5)
. (7.5)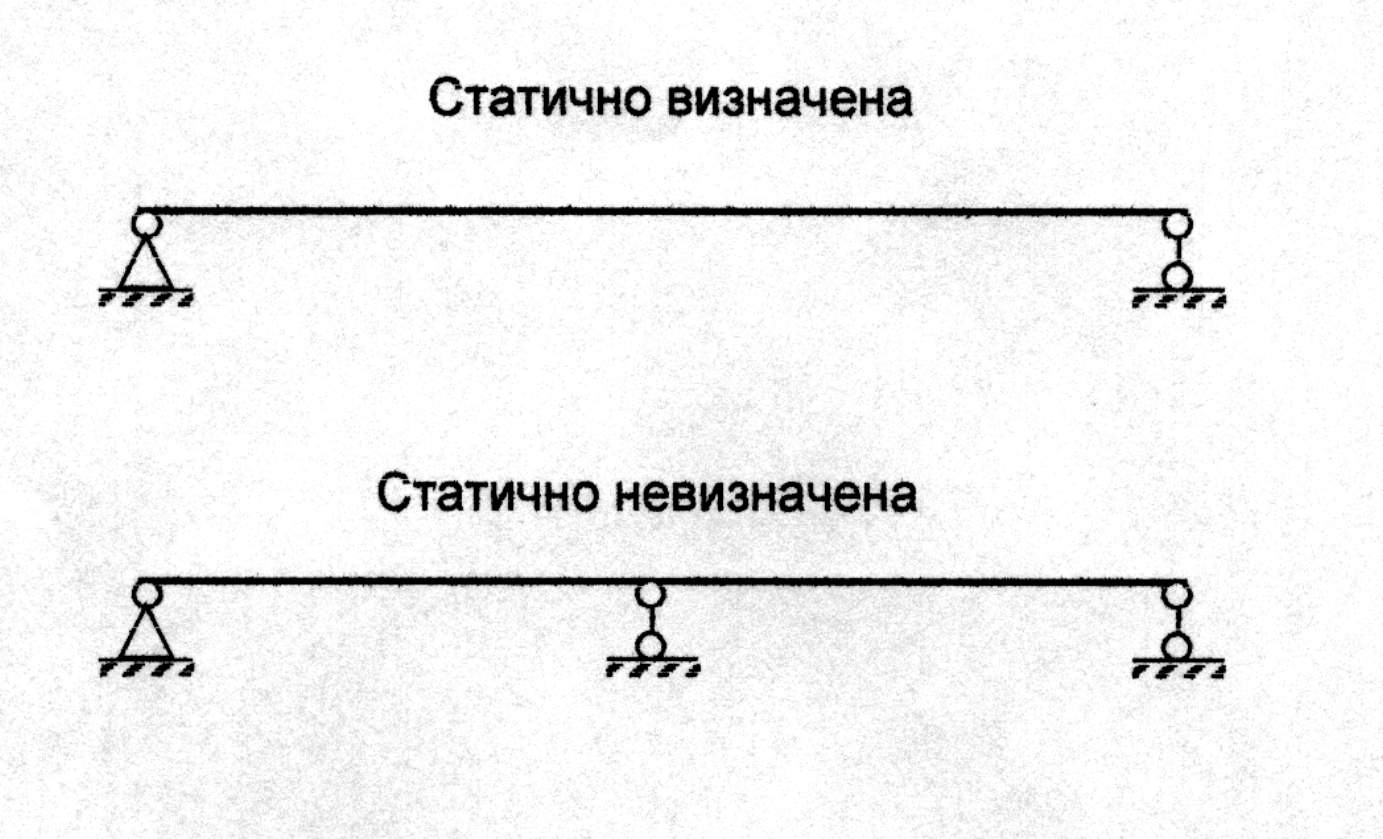
 знаходять за формулою
знаходять за формулою ,
,
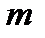 - кількість реакцій у в’язах, що накладені на балку;
- кількість реакцій у в’язах, що накладені на балку; 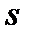 - кількість рівнянь рівноваги, що можна скласти для даної балки. Наприклад, для балки, що зображена на рис.8.2,б
- кількість рівнянь рівноваги, що можна скласти для даної балки. Наприклад, для балки, що зображена на рис.8.2,б  , тобто така балка двічі статично невизначена.
, тобто така балка двічі статично невизначена.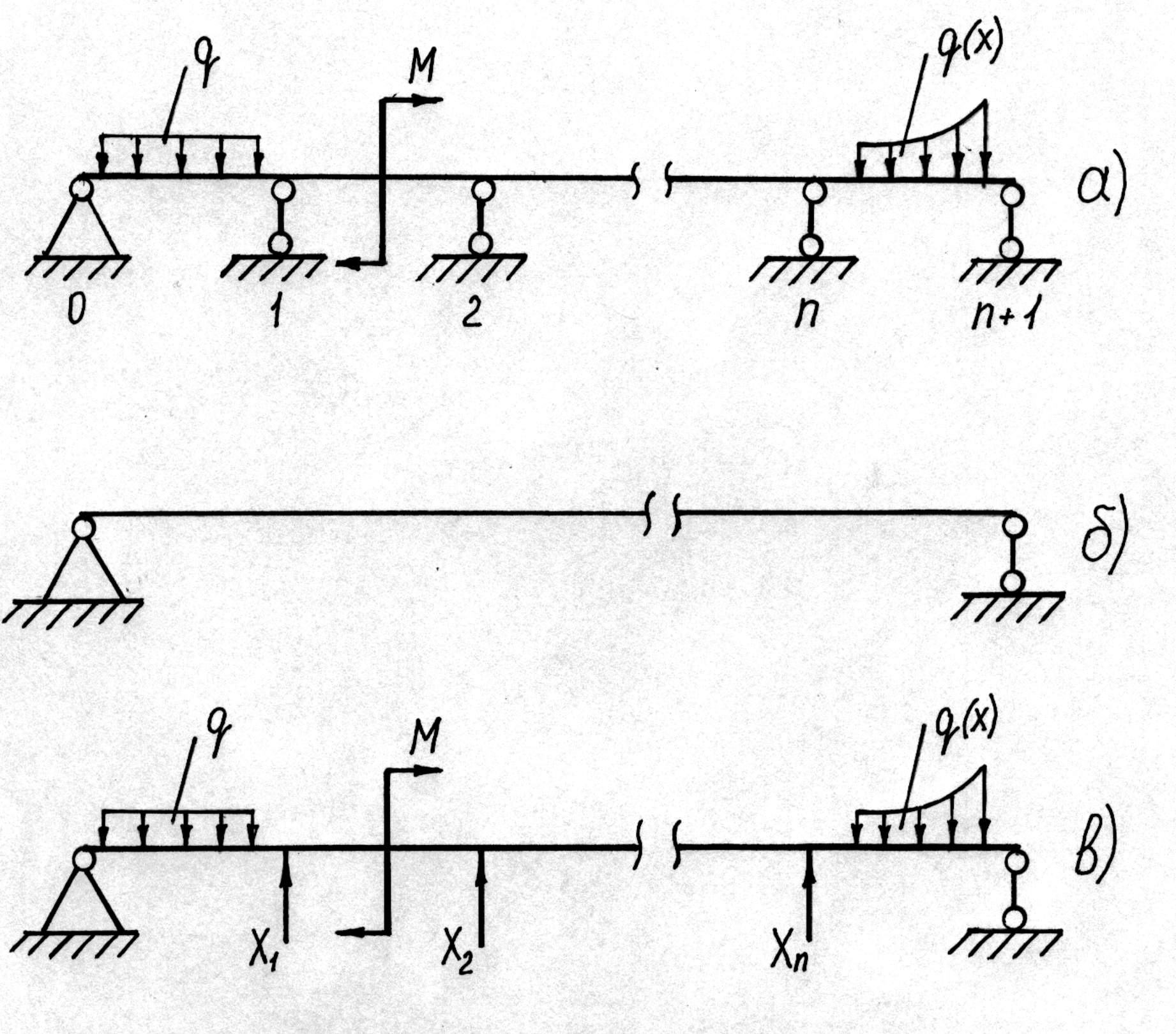 Рисунок 8.3
Рисунок 8.3
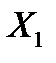 ,
, 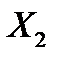 , ...,
, ..., 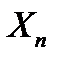 , що замінюють вплив на балку видалених в’язей, отримаємо еквівалентну систему (рис. 8.3,в).
, що замінюють вплив на балку видалених в’язей, отримаємо еквівалентну систему (рис. 8.3,в).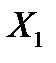 ,
, 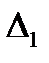 , ...,
, ..., 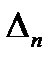 у вигляді суми прогинів, що викликані окремо кожною невідомою силою
у вигляді суми прогинів, що викликані окремо кожною невідомою силою  :
: . (8.1)
. (8.1)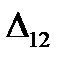 означає прогин точки прикладання сили
означає прогин точки прикладання сили 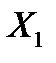 в напрямку її дії від сили
в напрямку її дії від сили 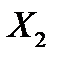 ;
; 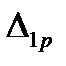 - те ж саме, тільки від зовнішнього навантаження і т.д. Прогини
- те ж саме, тільки від зовнішнього навантаження і т.д. Прогини 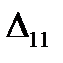 ,
, 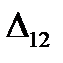 , ...,
, ...,  можна записати як добутки питомого прогину
можна записати як добутки питомого прогину 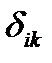 , що викликаний дією одиничної сили, на величину відповідної сили.
, що викликаний дією одиничної сили, на величину відповідної сили. ;
;  ;
; 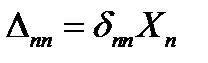 ,
,
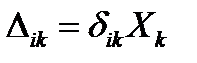 .
.
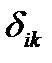 ,
, 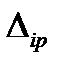 , що входять до канонічних рівнянь, можна визначити у будь-який зручний спосіб. Зазвичай користуються інтегралом Мора, який частіш за все обчислюють за способом Верещагіна. Для цього в основній системі будують епюри згинних моментів окремо від заданого зовнішнього навантаження (так звана грузова епюра
, що входять до канонічних рівнянь, можна визначити у будь-який зручний спосіб. Зазвичай користуються інтегралом Мора, який частіш за все обчислюють за способом Верещагіна. Для цього в основній системі будують епюри згинних моментів окремо від заданого зовнішнього навантаження (так звана грузова епюра 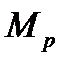 ) і від кожної одиничної сили (так звані одиничні епюри: від
) і від кожної одиничної сили (так звані одиничні епюри: від  - епюра
- епюра 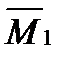 , від
, від 
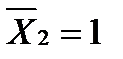 - епюра
- епюра 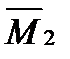 , від
, від 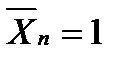 - епюра
- епюра 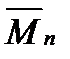 ).
). ,
, 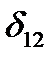 , ...,
, ...,  необхідно епюри
необхідно епюри  ;
; 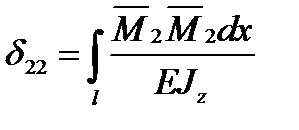 ; ...;
; ...; 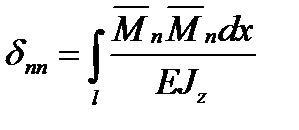 .
.
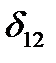 ,
, 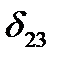 , ...,
, ..., 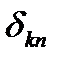 необхідно епюри
необхідно епюри 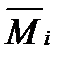 пере-
пере- , ...,
, ..., 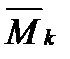 за способом Верещагіна, або
за способом Верещагіна, або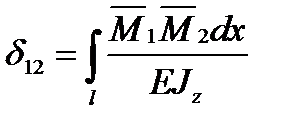 ;
; 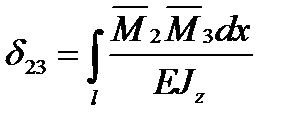 ; ...;
; ...; 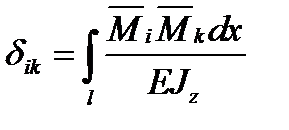 .
.
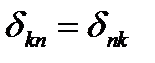 .
.
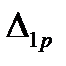 ,
,  , ...,
, ..., 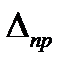 необхідно грузову епюру
необхідно грузову епюру  ;
; 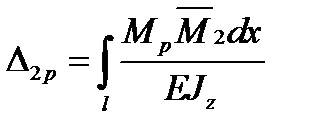 ; ...;
; ...; 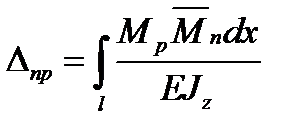 .
.
 .
.
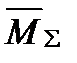 на одиничну епюру
на одиничну епюру 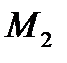 - суму коефіцієнтів другого рівняння і т.д.:
- суму коефіцієнтів другого рівняння і т.д.: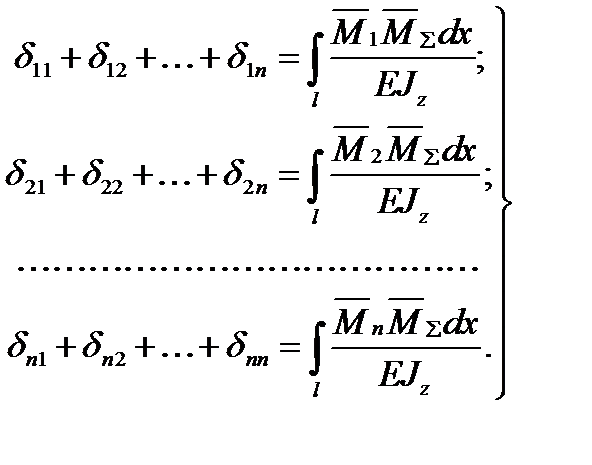
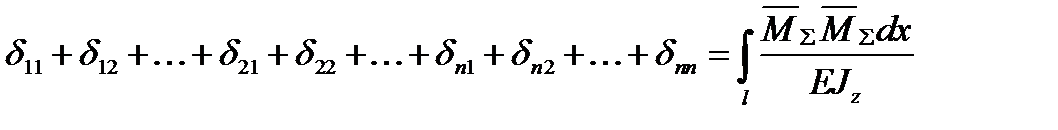 .
.
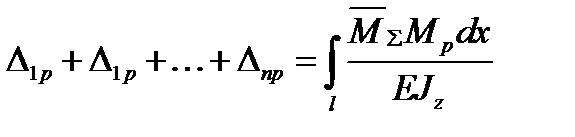 .
.
 Рисунок 10.1
Рисунок 10.1
 ,
,
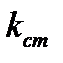 - коефіцієнт запасу стійкості.
- коефіцієнт запасу стійкості.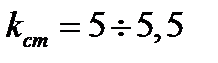 ; для дерев’яних стержнів
; для дерев’яних стержнів 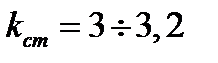 .
.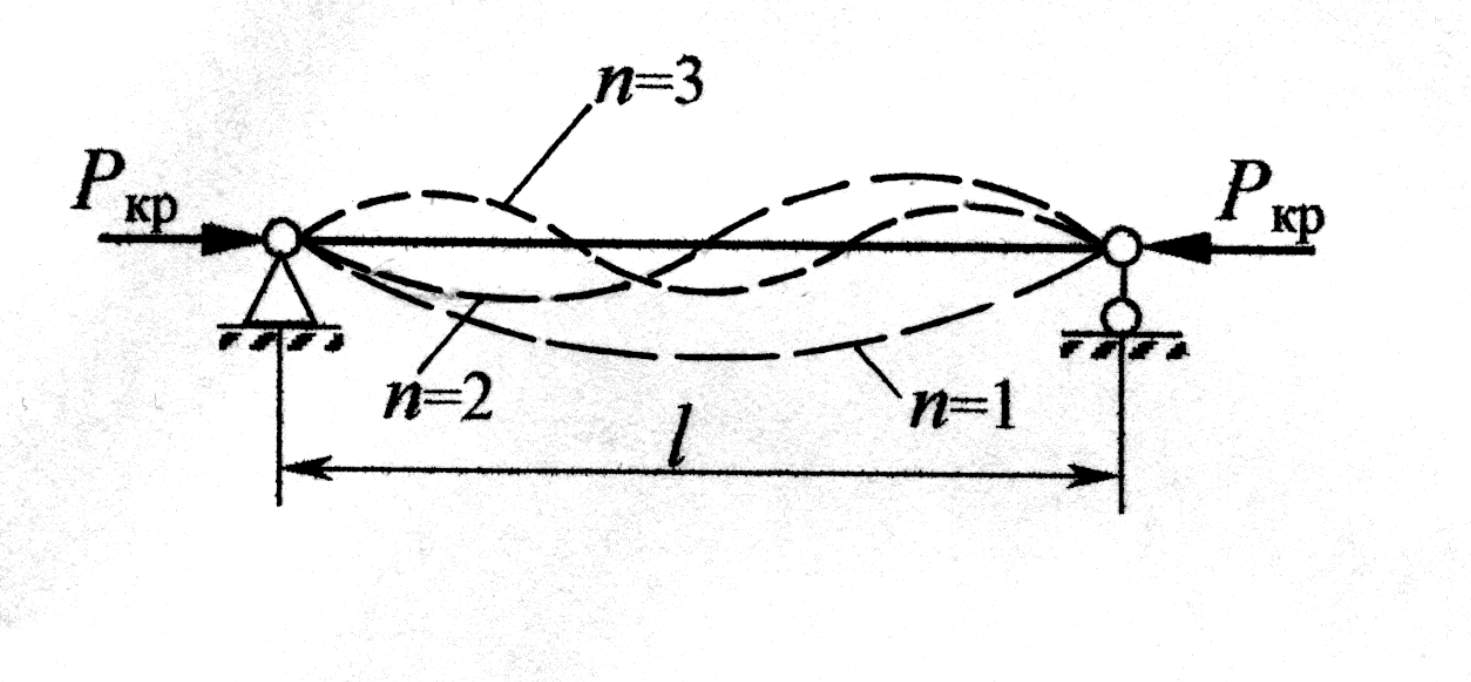 Рисунок 10.3
Рисунок 10.3
 Рисунок 10.2
Рисунок 10.2
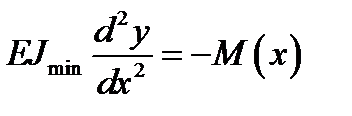 ,
,
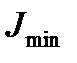 - мінімальний момент інерції поперечного перерізу стержня;
- мінімальний момент інерції поперечного перерізу стержня; 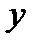 - відхилення центра ваги довільного перерізу від початкового положення на прямій осі;
- відхилення центра ваги довільного перерізу від початкового положення на прямій осі; 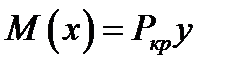 - згинний момент у довільному перерізі зігнутого стержня.
- згинний момент у довільному перерізі зігнутого стержня.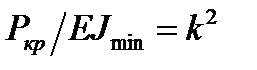 і дістанемо лінійне однорідне диференціальне рівняння
і дістанемо лінійне однорідне диференціальне рівняння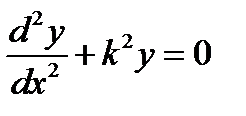 .
.
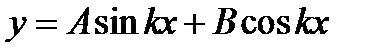 ,
,
 ;
; 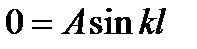 .
.
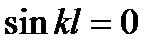 ,
,
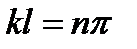 ,
,
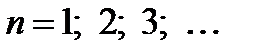 - довільне ціле число.
- довільне ціле число.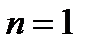 :
: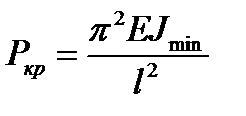 .
.
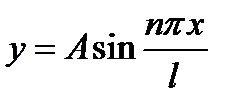 .
.
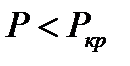 , то стержень має лише одну – прямолінійну форму рівноваги, що є стійкою.
, то стержень має лише одну – прямолінійну форму рівноваги, що є стійкою.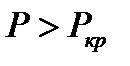 , то поряд із прямолінійною існує інша – криволінійна форма рівноваги, причому прямолінійна форма рівноваги нестійка, а стійкою є викривлена форма рівноваги. В таких випадках кажуть, що відбувається біфуркація рівноважних станів стержня.
, то поряд із прямолінійною існує інша – криволінійна форма рівноваги, причому прямолінійна форма рівноваги нестійка, а стійкою є викривлена форма рівноваги. В таких випадках кажуть, що відбувається біфуркація рівноважних станів стержня.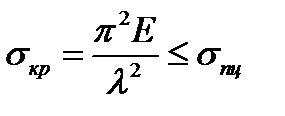 ,
,
 - границя пропорційності матеріалу стержня.
- границя пропорційності матеріалу стержня. .
.
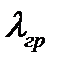 , при зменшенні якої формула Ейлера стає непридатною. Бачимо, що гранична гнучкість стержня є його фізико-механічною характеристикою і залежить від модуля пружності і границі пропорційності. Для стержнів, виготовлених з маловуглецевої сталі Ст3, при модулі пружності
, при зменшенні якої формула Ейлера стає непридатною. Бачимо, що гранична гнучкість стержня є його фізико-механічною характеристикою і залежить від модуля пружності і границі пропорційності. Для стержнів, виготовлених з маловуглецевої сталі Ст3, при модулі пружності 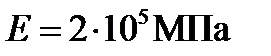 і границі пропорційності
і границі пропорційності 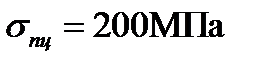 гранична гнучкість
гранична гнучкість ,
,
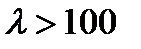 . Відповідно для матеріалів з іншими механічними характеристиками граничні гнучкості матимуть інші значення.
. Відповідно для матеріалів з іншими механічними характеристиками граничні гнучкості матимуть інші значення.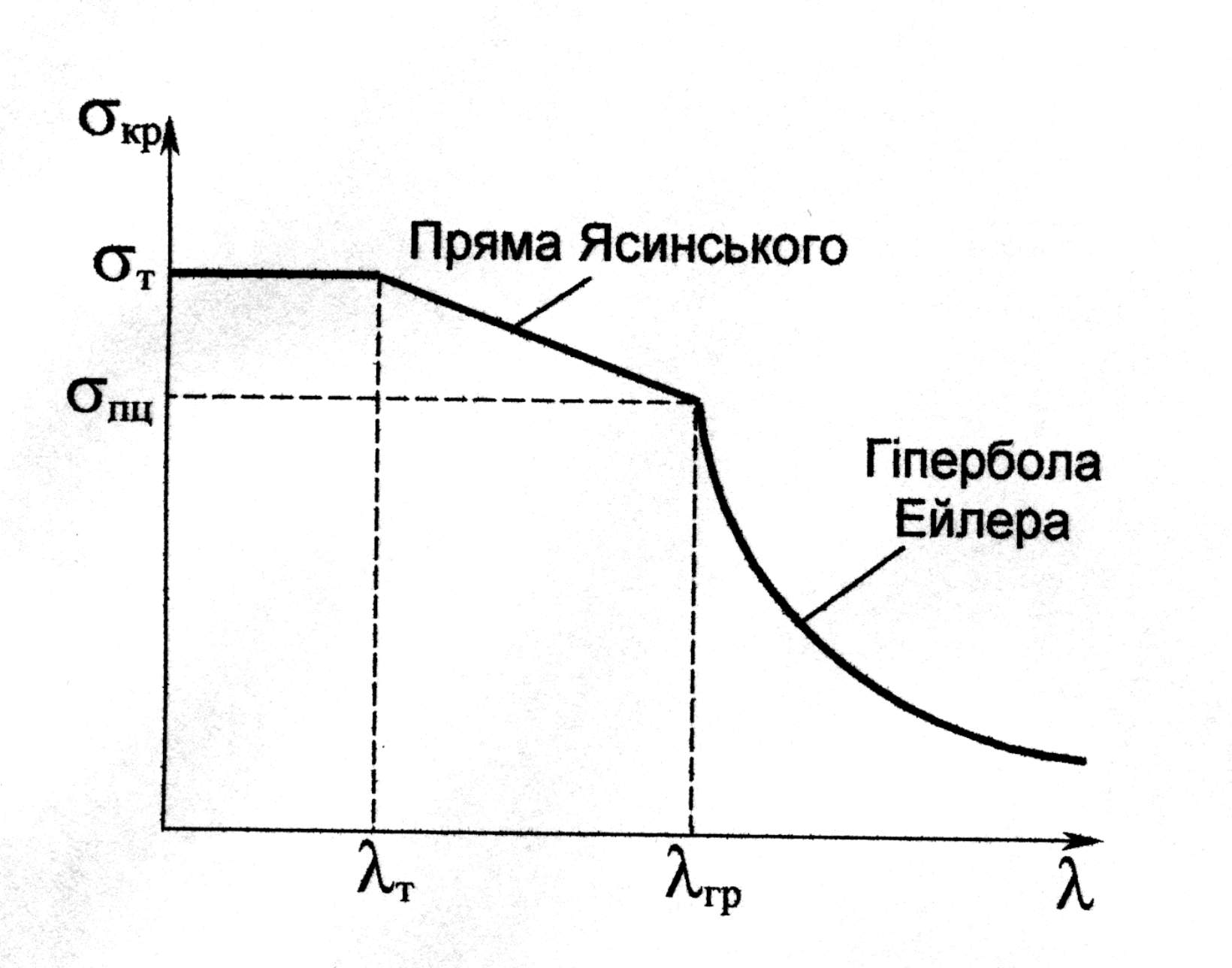 Рисунок 10.6
Рисунок 10.6
 ,
,
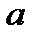 ,
, 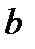 та
та  - коефіцієнти, що залежать від матеріалу стержня і визначаються експериментально (для пластичних матеріалів
- коефіцієнти, що залежать від матеріалу стержня і визначаються експериментально (для пластичних матеріалів 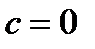 ).
).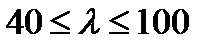 .
. на стійкість не розраховують, оскільки відповідні критичні напруження для них перевищують границю текучості, тобто руйнування таких стержнів відбувається внаслідок втрати міцності (рис.10.6 ділянка паралельна осі абсцис).
на стійкість не розраховують, оскільки відповідні критичні напруження для них перевищують границю текучості, тобто руйнування таких стержнів відбувається внаслідок втрати міцності (рис.10.6 ділянка паралельна осі абсцис). .
.
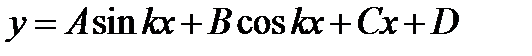 .
.
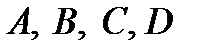 визначають з граничних умов. Наприклад, для другого випадку закріплення (рис. 10.4,б):
визначають з граничних умов. Наприклад, для другого випадку закріплення (рис. 10.4,б): ;
;  ;
;  ;
; 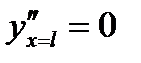 .
.

 .
.
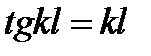 .
.
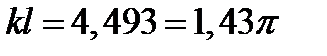 , тоді
, тоді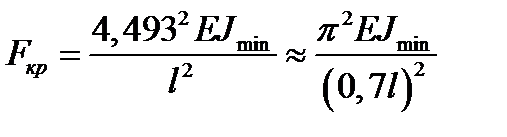 .
.
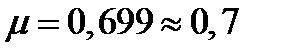 ;
; 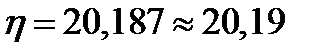 . Аналогічно отримують значення коефіцієнтів, що вказані на рис. 10.4, при інших способах закріплення стержня.
. Аналогічно отримують значення коефіцієнтів, що вказані на рис. 10.4, при інших способах закріплення стержня. Рисунок 10.5
Рисунок 10.5
 ;
;  ,
,
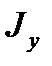 та
та 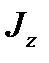 - головні моменти інерції перерізу стержня.
- головні моменти інерції перерізу стержня.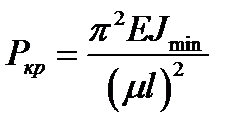 ,
або
,
або
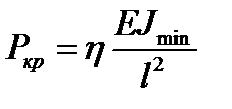 ,
,
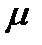 - коефіцієнт зведення довжини стержня (коефіцієнт Ясинського), що чисельно рівний величині, оберненій числу півхвиль синусоїди, по якій згинається стержень;
- коефіцієнт зведення довжини стержня (коефіцієнт Ясинського), що чисельно рівний величині, оберненій числу півхвиль синусоїди, по якій згинається стержень; 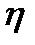 - коефіцієнт стійкості, що визначають за формулою
- коефіцієнт стійкості, що визначають за формулою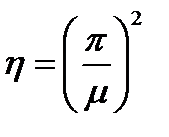 .
.
 називають зведеною довжиною. Це умовна довжина шарнірно обіпертого стержня, для якого критична сила дорівнює критичній силі для заданого стержня довжиною
називають зведеною довжиною. Це умовна довжина шарнірно обіпертого стержня, для якого критична сила дорівнює критичній силі для заданого стержня довжиною 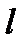 .
.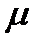 і
і 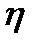 залежать від трьох факторів:
залежать від трьох факторів: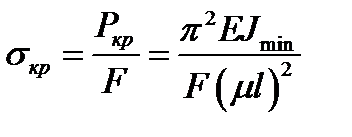 .
.
 є квадратом мінімального радіуса інерції
є квадратом мінімального радіуса інерції 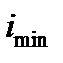 , одержимо
, одержимо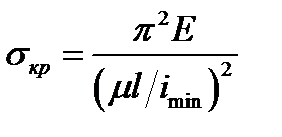 .
.
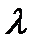 , що називається гнучкістю стержня і дорівнює відношенню зведеної довжини до мінімального радіуса інерції поперечного перерізу:
, що називається гнучкістю стержня і дорівнює відношенню зведеної довжини до мінімального радіуса інерції поперечного перерізу: .
.
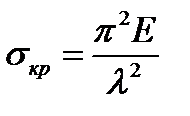 .
.
 :
: ,
,
 .
.
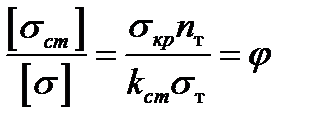 ,
,
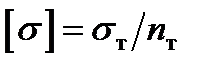 - допустиме напруження на міцність при стисканні;
- допустиме напруження на міцність при стисканні; 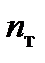 - коефіцієнт запасу міцності.
- коефіцієнт запасу міцності.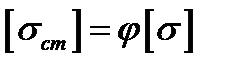 ,
,
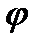 - коефіцієнт зменшення основного допустимого напруження на міцність при розрахунку на стійкість.
- коефіцієнт зменшення основного допустимого напруження на міцність при розрахунку на стійкість.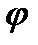 для кожного матеріалу можна визначити при будь-якому значенні гнучкості й подати у вигляді таблиці або графіку залежності
для кожного матеріалу можна визначити при будь-якому значенні гнучкості й подати у вигляді таблиці або графіку залежності 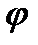 від
від 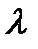 .
. .
.
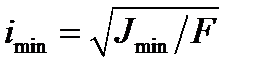 ;
;
 ;
;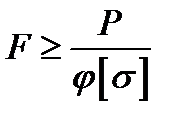 .
.
 та коефіцієнт
та коефіцієнт 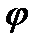 , який залежить від невизначених ще розмірів перерізу, його форми та довжини стержня. Тому задачу розв’язують методом послідовних наближень з перевіркою проміжних результатів за допомогою умови стійкості в такій послідовності:
, який залежить від невизначених ще розмірів перерізу, його форми та довжини стержня. Тому задачу розв’язують методом послідовних наближень з перевіркою проміжних результатів за допомогою умови стійкості в такій послідовності: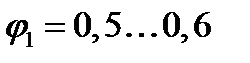 та обчислюють площу
та обчислюють площу  перерізу стержня:
перерізу стержня: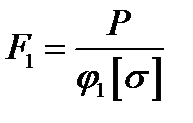 ;
;
 .
.
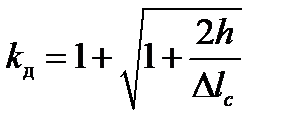 ,
,
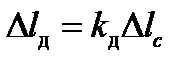 ,
,
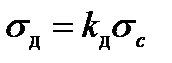 ,
,
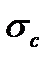 - напруження, що виникає при статичному прикладанні навантаження.
- напруження, що виникає при статичному прикладанні навантаження.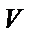 у момент зіткнення. Знаючи, що
у момент зіткнення. Знаючи, що 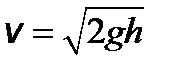 , звідки
, звідки 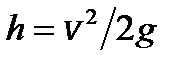 , матимемо
, матимемо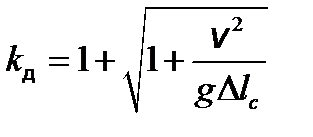 .
.
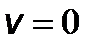 ,
,  ), то
), то 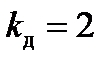 , а
, а 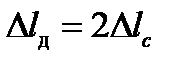 ;
;  .
. , то вираз для динамічного коефіцієнта спрощується:
, то вираз для динамічного коефіцієнта спрощується: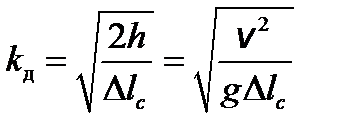 .
.
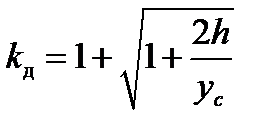
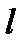 з висоти
з висоти  , позначимо
, позначимо  . Оскільки швидкість падаючого вантажу в кінці удару дорівнюватиме нулю, то зміна кінетичної енергії дорівнюватиме роботі сили
. Оскільки швидкість падаючого вантажу в кінці удару дорівнюватиме нулю, то зміна кінетичної енергії дорівнюватиме роботі сили 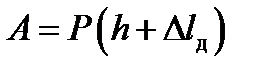 ,
,
 .
.
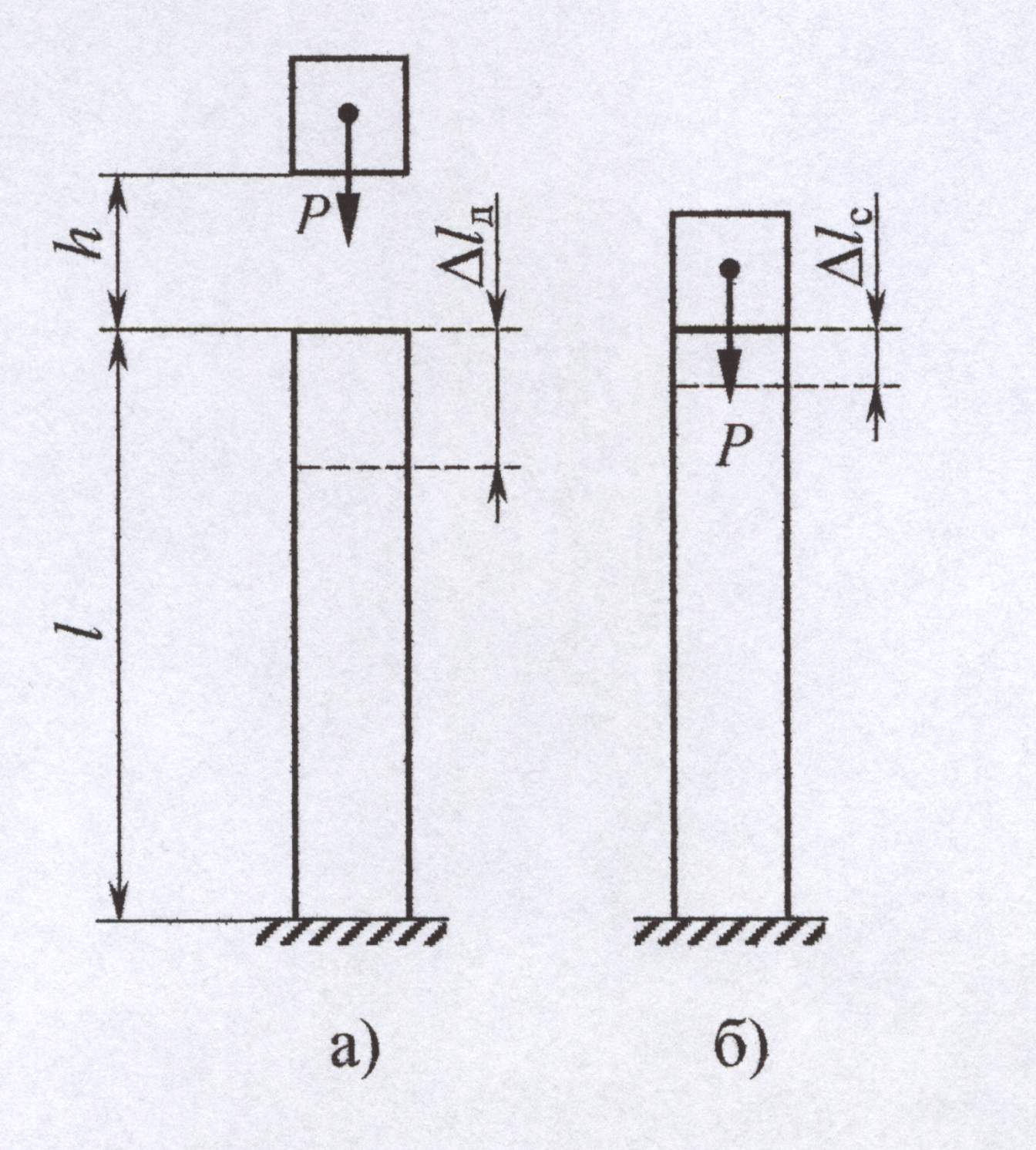 Рисунок 12.1
Рисунок 12.1
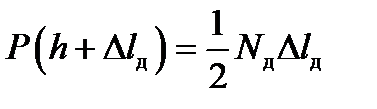 .
.
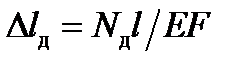 , визначимо
, визначимо  . (12.4)
. (12.4)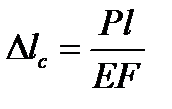 ,
,
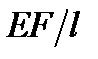 прийдемо до зведеного квадратного рівняння
прийдемо до зведеного квадратного рівняння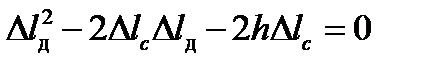 .
.
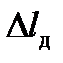 , матимемо
, матимемо .
.
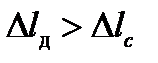 ).
). Рисунок 12.2
Рисунок 12.2
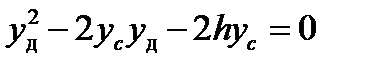 .
.
 і
і 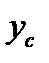 .
. ,
,