 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Додавання коливань однакового напряму
Гармонічні коливання
Коливаннями називаються рухи або процеси, які характеризуються певною повторюваністю в часі. Фізична природа коливань може бути різною, тому розрізняють коливання механічні, електромагнітні й ін. Але всі вони описуються однаковими характеристиками й однаковими рівняннями. Мінімальний проміжок часу, через який повторюється положення тіла в коливальному русі, називають періодом Т.
Прикладом гармонічного коливання може бути рух проекції точки, яка рівномірно рухається по колу, на будь-яку пряму в площині руху (рис. 39). Якщо радіус кола R, а кутова швидкість точки
бо через час одного оберту точки М, зміщення її проекції N точно повторюватиметься; кількість коливань за секунду З наведених означень випливають такі залежності:
Рівняння гармонічного коливального руху в загальному вигляді буде
Вираз у дужках, що входить під знак синуса, називають фазою. Фаза визначає положення точки в коливальному русі в будь-який момент часу. Швидкість точки в гармонічному коливанні знайдемо як першу похідну від зміщення за часом:
Прискорення точки в гармонічному коливанні
Крім аналітичного відображення гармонічного коливання у вигляді рівняння координати х точки N, його можна також відобразити у вигляді зміни проекції вектора амплітуди А, що рівномірно обертається з кутовою швидкістю
Динаміка гармонічних коливань
Розглянемо механічні системи коливання яких відбувається за гармонічним законом. До них можна віднести пружинний, математичний та фізичний маятники. Математичним маятником називають матеріальну точку, підвішену на невагомій і нерозтяжній нитці, що коливається у вертикальній площині під дією сили тяжіння. Нехай маса маятника т, а довжина нитки l. З відхиленням маятника від положення рівноваги виникає повертаюча сила, яка є рівнодійною сил діючих на матеріальну точку – сили тяжіння та сили натягу з боку нитки. При малих кутових відхиленнях
Одержимо рівняння руху маятника на підставі другого закону динаміки Оскільки на маятник діє одна результуюча сила, то
Введемо позначення
Розв‘язком даного рівняння є інтегральне рівняння виду
де
визначається довжиною маятника і прискоренням вільного падіння і не залежить від маси і амплітуди коливань. Математичний маятник використовують для вимірювання прискорення вільного падіння.Земна кора в різних місцях має неоднаковий склад, тому в місцях, де кора має більшу густину, прискорення вільного падіння збільшується. Вимірюючи його математичним маятником, розвідують корисні копалини.
Пружний маятник зображений на рис. 41. Це тіло масою m, що прикріплено до пружини. Якщо тіло відхилити від положення рівноваги, то на нього буде діяти пружна сила, пропорційна зміщенню F=-kx, яка повертає тіло до положення рівноваги. Складемо рівняння руху пружного маятника. Оскільки на маятник діє одна сила – сила пружності, то
Введемо позначення
Розв‘язком даного рівняння, як і для математичного маятника, є інтегральне рівняння виду
Період коливань пружного маятника визначається формулою
і залежить тільки від маси тіла та жорсткості пружини. Фізичним маятником називають тверде тіло довільної форми, яке коливається під дією тяжіння навколо горизонтальної осі. Якщо маятник вивести з положення рівноваги (рис.42), то на нього діятиме повертаючий момент сили тяжіння М, знак якого протилежний знаку кута відхилення маятника, а саме:
де Використовуючи основний закон динаміки обертального руху
де
Це рівняння цілком аналогічне рівнянню математичного та пружного маятників. Отже і розв’язок його можна подати у вигляді Циклічна частота коливань а період коливань Формулу періоду коливання фізичного маятника нерідко використовують як робочу формулу для визначення прискорення вільного падіння або моменту інерції тіла. Для кожного фізичного маятника можна підібрати такий математичний маятник, який матиме однаковий період коливання з даним фізичним. Довжина такого математичного маятника, який має однаковий період з даним фізичним, називається зведеною довжиною фізичного маятника. З рівності періодів коливання цих маятників можна знайти вираз для зведеної довжини
Точка на фізичному маятнику О1, що відповідає зведеній довжині, називається центром коливань. Центр коливань і точка підвішування — спряжені точки. Якщо їх поміняти ролями, то період фізичного маятника не зміниться.
Енергія коливального руху
Щоб надати матеріальній точці коливального руху, треба вивести її з положення рівноваги. Для цього виконують певну роботу проти повертаючої сили. Ця робота буде мірою потенціальної енергії, наданої точці ззовні:
Потенціальна енергія точки в коливальному русі пропорційна квадрату зміщення. Після припинення дії зовнішньої сили точка повертатиметься до положення рівноваги під дією квазіпружної сили. У міру зменшення
зміщення, відповідно до закону збереження енергії, потенціальна енергія точки перетворюватиметься в кінетичну енергію. Оскільки зміщення точки
Кінетичну енергію точки з масою m і швидкістю V запишемо так:
У положеннях крайнього зміщення потенціальна енергія максимальна, а кінетична дорівнює нулю. З рухом до положення рівновагі потенціальна енергія зменшується, а кінетична збільшується; у момент рівновагі потенціальна енергія дорівнює нулю, а кінетична набуває максимального значення. За рахунок кінетичної енергії точка далі зміщується в протилежний бік. Такі періодичні (але не гармонічні) коливання потенціальної і кінетичної енергії відбуваються в процесі гармонічного коливання точки. Повна енергія точки в коливальному русі складається із суми потенціальної і кінетичної енергії
Отже, енергія точки в коливальному русі пропорційна квадрату амплітуди і квадрату частоти. Якщо система ізольована від інших зовнішніх впливів і точка коливається без тертя, то згідно з законом збереження енергія Е коливального руху точки залишається сталою.
Затухаючі коливання
Практично всяке коливання , якщо воно не підтримується ззовні, затухає. Причинами є сили тертя, які перетворюють механічну енергію у інші види енергії. Найістотніше впливає на коливання тіла опір середовища. Сила опору середовища при малих швидкостях пропорційна швидкості.
де г — коефіцієнт опору; знак мінус показує, що сила опору завжди напрямлена проти напрямку руху. Розглянемо пружний маятник і складемо рівняння динаміки його руху, враховуючи, що на маятник діють дві сили – сила пружності та сила опору середовища.
Поділивши друге рівняння на масу т і ввівши позначення
дістанемо однорідне диференціальне рівняння другого порядку. Загальний розв'язок диференціального рівняння для затухаючих коливань (18) має такий вигляд:
де
Коли опір середовища значний, тіло повільно без коливання повертається в положення рівноваги.
Графік затухаючих коливань зображено на рис. 43. Швидкість затухання характеризують логарифмічним декрементом затухання, тобто логарифмом відношення двох послідовних амплітуд
Логарифмічний декремент — безрозмірне число, яке дорівнює, наприклад, для камертона 10-3, для інших звукових коливальних систем—близько 0,1. Щоб коливання не затухали, до системи треба підводиш енергію ззовні. Енергію можна поповнювати додатковими зовнішніми поштовхами в такт коливанням. Практично використовуються такі пристрої, за допомогою яких сама коливальна система в потрібний момент зумовлює зовнішній поштовх. Таку систему називають автоколивальною, а її коливання автоколиваннями. Прикладом автоколивальної системи є годинник.
Вимушені коливання
Якщо коливальна система зазнала лише зовнішнього поштовху або була виведена з положення рівноваги і залишена сама на себе, то її коливання називають вільними. Якби не було сил опору, то ці коливання називали б власними. Період і частота власних коливань залежать насамперед від речовини і геометричних особливостей тіла (камертон, струна, міст і т.д.). Практично всякі вільні коливання є затухаючими. Не затухаючі коливання виникають під дією зовнішньої періодично змінної сили
Таку силу називають змушувальною, а коливання, що виникають під її дією, вимушеними. Вимушених коливань зазнає мембрана гучномовця, фундамент поршневого двигуна, міст від поштовхів прохожих та ін. Складемо рівняння динаміки вимушених коливань. При цьому врахуємо, що крім змушувальної сили на систему діють також ква-зіпружна сила і сила опору середовища, що, як і раніше, сила опору пропорційна швидкості руху. Рівняння руху буде таке:
Поділивши це рівняння на масу і ввівши позначення
дістанемо неоднорідне лінійне диференціальне рівняння другого порядку
Розв'язок такого рівняння (після деякого періоду стабілізації) шукатимемо в такому вигляді:
Протягом певного часу встановлюються коливання такого самого характеру і частоти, як і коливання змушувальної сили, лише з деяким зсувом по фазі Амплітуда вимушених коливань визначається формулою:
а зсув фаз
Вимушені коливання є гармонічні коливання, частота яких дорівнює частоті змушувальної сили. Амплітуда вимушених коливань залежить не тільки від амплітудного значення змушувальної сили, а й від її частоти коливання. При певній частоті змушувальної сили рівняння (26):
Підставивши це значення частоти в (26), знайдемо резонансне значення амплітуди
З виразу (27) бачимо, що коли опір середовища малий то резонансна частота майже збігається з частотою власних коливань. У ньому випадку амплітуда вимушених коливань стає дуже великою.
Явище резонансу відіграє істотну роль у техніці. Його використовують в акустиці й радіотехніці, у приладах для вимірювання частоти і т.д. Проте явище резонансу може спричиняти руйнування споруд і машин. Треба враховувати, що періодичні поштовхи від поршневих машин, силових валів турбін, гребних гвинтів і пропелерів передаються на фундаменти та інші частини машини. Тут резонанс дуже небезпечний. Тому, наприклад, власна частота вібрацій корпуса корабля або крил літака повинна дуже відрізнятися від частоти змушувальної сили, зумовленої обертанням силових гвинтів. Усе це враховують, конструюючи машини й споруди. В окремих випадках резонанс призводив до руйнування мостів, коли по них проходила колона військ. Це пояснюється тим, що частота відбивання кроку збігалася з резонансною частотою коливань моста. Величина зсуву фаз залежить не тільки від сили опору, а й від співвідношення частот власних коливань системи сили Коли
Додавання коливань однакового напряму Можливі випадки, коли тіло перебуває одночасно в кількох коливаннях. Як приклад можна назвати коливання кульки, підвішеної на пружині у вагоні. Кулька коливається на пружині відносно точки підвішування і разом з вагоном коливається на ресорах відносно землі. Обидва ці коливання мають однаковий вертикальний напрям. Знайдемо результуючий рух точки, яка одночасно перебуває в двох гармонічних коливаннях однакової частоти і однакового напрямку, заданих рівняннями
У цьому виразі амплітуда А та початкова фаза
З (29) видно, що амплітуда результуючого коливання залежить від різниці фаз складових коливань. Якщо Коли додають гармонічні коливання з різними частотами, вектори амплітуд Інтерес становить додавання двох гармонічних коливань з близькими частотами. Для спрощення викладу припустимо, що амплітуди їх однакові, а початкові фази коливань дорівнюють нулю. За цієї умови рівняння складових коливань матимуть такий вигляд: Якщо додати ці два вирази і застосувати формулу суми синусів, дістанемо
Порівнявши цей вираз з рівнянням гармонічного коливання, можна дійти висновку, що результуюче коливання відбувається з частотою, яка дорівнює півсумі частот, але його амплітуда
в свою чергу, змінюється з частотою пульсацій, що дорівнює піврізниці частот складових коливань. Таке результуюче коливання називають биттям.
Поиск по сайту: |
 Серед різних коливальних рухів у природі й техніці важливе значення мають гармонічні коливання. Гармонічним називають коливальний рух, у якому зміщення матеріальної точки від положення рівноваги змінюється за рівнянням синуса (косинуса). Коливання в природі й техніці часто дуже близькі до гармонічних, а, крім того, всякі періодичні зміни величин із складнішою залежністю від часу можна розкласти на гармонічні коливання.
Серед різних коливальних рухів у природі й техніці важливе значення мають гармонічні коливання. Гармонічним називають коливальний рух, у якому зміщення матеріальної точки від положення рівноваги змінюється за рівнянням синуса (косинуса). Коливання в природі й техніці часто дуже близькі до гармонічних, а, крім того, всякі періодичні зміни величин із складнішою залежністю від часу можна розкласти на гармонічні коливання. , то координата її проекції
, то координата її проекції (1)
(1) де х —зміщення точки від положення рівноваги;Найбільше значення зміщення точки в коливальному русі (х = R= А) називають амплітудою; період коливання Т точки, N, очевидно, буде
де х —зміщення точки від положення рівноваги;Найбільше значення зміщення точки в коливальному русі (х = R= А) називають амплітудою; період коливання Т точки, N, очевидно, буде , (2)
, (2) —циклічна (або колова) частота коливання;
—циклічна (або колова) частота коливання; називають частотою коливань.
називають частотою коливань. (3)
(3)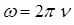 . (4)
. (4) (5)
(5) - початкова фаза, яка визначає положення точки в момент часу t=0.
- початкова фаза, яка визначає положення точки в момент часу t=0. (6)
(6) (7)
(7) чисельно дорівнює зміщенню точки N в коливальному русі. Звідси зрозуміло, чому
чисельно дорівнює зміщенню точки N в коливальному русі. Звідси зрозуміло, чому  , де
, де  (рад) — кутове відхилення маятника.
(рад) — кутове відхилення маятника. , тому повертаючу силу можна записати у вигляді
, тому повертаючу силу можна записати у вигляді
 де х — зміщення маятника від положення рівноваги, а знак мінус показує, що повертаюча сила протилежна до напряму зміщення.
де х — зміщення маятника від положення рівноваги, а знак мінус показує, що повертаюча сила протилежна до напряму зміщення.
 , або
, або 
 і одержимо диференційне рівняння вільних коливань математичного маятника
і одержимо диференційне рівняння вільних коливань математичного маятника . (8)
. (8) , (9)
, (9) циклічна частота власних коливань маятника. Якщо підставити (9) у рівняння (8), то одержимо тотожність. Отже коливання математичного маятника з малими амплітудами є гармонічними. Період коливання математичного маятника
циклічна частота власних коливань маятника. Якщо підставити (9) у рівняння (8), то одержимо тотожність. Отже коливання математичного маятника з малими амплітудами є гармонічними. Період коливання математичного маятника (10)
(10) , або
, або

 і одержимо диференційне рівняння вільних коливань математичного маятника у вигляді
і одержимо диференційне рівняння вільних коливань математичного маятника у вигляді
 , (11)
, (11)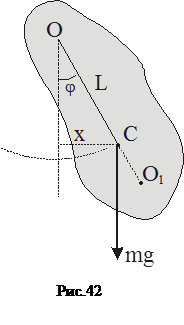

 — відстань центра маси від точки підвішування. При малих кутах відхилення
— відстань центра маси від точки підвішування. При малих кутах відхилення 
 ,
, - момент інерції маятника відносно осі обертання,
- момент інерції маятника відносно осі обертання,  - кутове прискорення, одержимо диференційне рівняння вільних коливань фізичного маятника
- кутове прискорення, одержимо диференційне рівняння вільних коливань фізичного маятника
 (12)
(12) , (13)
, (13) (14)
(14) фізичного маятника:
фізичного маятника:

 і коефіцієнт квазіпружної сили
і коефіцієнт квазіпружної сили  , то потенціальну енергію точки в коливальному русі можна визначити за формулою
, то потенціальну енергію точки в коливальному русі можна визначити за формулою (15)
(15) (16)
(16) (17)
(17)
 (18)
(18)
 (19)
(19)
 — частота затухаючих коливань. Період затухаючих коливань визначається за формулою
— частота затухаючих коливань. Період затухаючих коливань визначається за формулою (20)
(20) коливання не виникає, зміщене
коливання не виникає, зміщене (21)
(21) (22)
(22) (23)
(23)

 (24)
(24) (25)
(25) . Однією з причин зсуву є сила опору.
. Однією з причин зсуву є сила опору. , (26)
, (26) .
. амплітуда вимушених коливань різко зростає, досягаючи максимального значення. Настає явище резонансу. Резонансну частоту можна визначити з умови максимуму амплітуди
амплітуда вимушених коливань різко зростає, досягаючи максимального значення. Настає явище резонансу. Резонансну частоту можна визначити з умови максимуму амплітуди  , або мінімуму підкореневого виразу в знаменнику
, або мінімуму підкореневого виразу в знаменнику (27)
(27)
 Залежність амплітуди вимушених коливань від частоти для різних коефіцієнтів затухання зображено на рис. 44. Із зростанням коефіцієнта затухання максимум резонансної кривої швидко опускається і крива згладжується. Явище резонансу стає малопомітним.
Залежність амплітуди вимушених коливань від частоти для різних коефіцієнтів затухання зображено на рис. 44. Із зростанням коефіцієнта затухання максимум резонансної кривої швидко опускається і крива згладжується. Явище резонансу стає малопомітним. і змушувальної
і змушувальної . Коли
. Коли  , то зсув фаз досягає
, то зсув фаз досягає  (за фазою зміщення відстає від сили). У цьому випадку змушувальна сила на всьому шляху коливання точки збігається за напрямом з рухом точки, тому виконує позитивну роботу, в результаті якої енергія системи збільшується. Такі умови характерні для явища резонансу.
(за фазою зміщення відстає від сили). У цьому випадку змушувальна сила на всьому шляху коливання точки збігається за напрямом з рухом точки, тому виконує позитивну роботу, в результаті якої енергія системи збільшується. Такі умови характерні для явища резонансу. зсув фаз наближається до
зсув фаз наближається до  , тобто коливання за фазою майже протилежні змушувальній силі. Коли зсув фаз відмінний від
, тобто коливання за фазою майже протилежні змушувальній силі. Коли зсув фаз відмінний від  , то на деяких дільницях змушувальна сила напрямлена проти руху точки, тому виконує негативну роботу, в результаті якої енергія точки частково зменшується. В цілому умови поповнення енергії системи менш сприятливі, ніж умови резонансу.
, то на деяких дільницях змушувальна сила напрямлена проти руху точки, тому виконує негативну роботу, в результаті якої енергія точки частково зменшується. В цілому умови поповнення енергії системи менш сприятливі, ніж умови резонансу. (28)
(28) Результуюче коливання х=х1+х2 одержимо графічним методом – методом векторних діаграм. Для цього з довільної точки О взятої на осі х, під кутом α1 (α2), рівним початковій фазі коливання, відкладають вектор А1 (А2), модуль якого дорівнює амплітуді А1 (А2) коливання що розглядається. Якщо цей вектор обертати з кутовою швидкістю
Результуюче коливання х=х1+х2 одержимо графічним методом – методом векторних діаграм. Для цього з довільної точки О взятої на осі х, під кутом α1 (α2), рівним початковій фазі коливання, відкладають вектор А1 (А2), модуль якого дорівнює амплітуді А1 (А2) коливання що розглядається. Якщо цей вектор обертати з кутовою швидкістю  , то проекція кінця вектора буде здійснювати гармонічні коливання. На рис.45 побудовані векторні діаграми коливань (28). Оскільки вектори А1 та А2 обертаються з постійною кутовою швидкістю
, то проекція кінця вектора буде здійснювати гармонічні коливання. На рис.45 побудовані векторні діаграми коливань (28). Оскільки вектори А1 та А2 обертаються з постійною кутовою швидкістю 
 відповідно задаються співвідношеннями
відповідно задаються співвідношеннями (29)
(29) (30)
(30) , то амплітуда результуючого коливання
, то амплітуда результуючого коливання  ; якщо
; якщо  , тобто складові коливання перебувають у протилежних фазах, то амплітуда результуючого коливання
, тобто складові коливання перебувають у протилежних фазах, то амплітуда результуючого коливання  .
. і
і 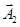 обертаються з різними кутовими швидкостями
обертаються з різними кутовими швидкостями  і
і  , тому результуючий вектор
, тому результуючий вектор  за. величиною змінюється; кутова швидкість його обертання теж змінюється, і залежно від співвідношення частот відбуваються різні складні коливальні процеси.
за. величиною змінюється; кутова швидкість його обертання теж змінюється, і залежно від співвідношення частот відбуваються різні складні коливальні процеси. (31)
(31) . (32)
. (32) ,
,