 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Інтегрування частинами. Теорема.Якщо функції і неперервно диференційовні, то має місце формула ⇐ ПредыдущаяСтр 2 из 2
Теорема.Якщо функції
Якщо врахувати, що
Отримана формула, що називається формулою інтегрування частинами, зводить відшукування первісної функції Наведемо два розповсюджених види інтегралів, які обчислюються за формулою інтегрування частинами: I. За II. За Приклад 2. Знайти інтеграли: 1) Розв’язання.1) цей інтеграл відноситься до виду I:
2) цей інтеграл відноситься до виду I:
3) даний інтеграл відноситься до виду II. Маємо:
Задача звелась до знаходження інтеграла від неправильного дробу. Поділимо чисельник (
Отже,
4)
Тут, як і в прикладі 2.3, зображення 5)
Останній перехід засновано на першій властивості інтеграла. Інтегрування підстановкою (заміна змінної) Введення нової змінної інтегрування часто зводить розглядуваний інтеграл до табличного. Нехай структура підінтегрального виразу в інтегралі
Тут припускається, що функції Іноді використовують другу форму правила підстановки, коли
Підстановка
де Вкажемо корисні підстановки для таких інтегралів: 1) 2) 3) 4) 5) 6) Приклад 3. Знайти інтеграли: 1) Розв’язання У кожному з цих інтегралів зробимо підстановку 1) 2) Зокрема
Приклад 4. Знайти інтеграли: 1) Розв’язання Усі ці інтеграли можуть бути зведені до модельних інтегралів з прикладу 3: 1) здійснимо підстановку
2) виконаємо підстановку
3) здійснимо заміну змінної
4) виконаємо підстановку
5) Визначений інтеграл
Поиск по сайту: |
 і
і  неперервно диференційовні, то має місце формула
неперервно диференційовні, то має місце формула
 , то попередню формулу можна записати у вигляді
, то попередню формулу можна записати у вигляді
 до відшукування первісної функції
до відшукування первісної функції  . Її застосування корисне тоді, коли друга задача більш проста. При обчисленні інтеграла
. Її застосування корисне тоді, коли друга задача більш проста. При обчисленні інтеграла 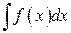 за формулою інтегрування частинами підінтегральна функція
за формулою інтегрування частинами підінтегральна функція  подається у вигляді добутку
подається у вигляді добутку  легко знаходилась.
легко знаходилась. ,
,  ,
, 
 , а за
, а за  ,
,  ,
,  ;
; ,
,  ,
, 
 ,
,  ,
,  , а за
, а за 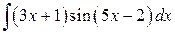 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.

 .
.
 .
.
 .
. ) на знаменник (
) на знаменник (  ):
):
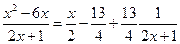 і тому
і тому
 .
.

 .
. можна дістати в результаті ділення. У наведеному вище розв’язанні застосовано штучний прийом.
можна дістати в результаті ділення. У наведеному вище розв’язанні застосовано штучний прийом.

 .
. є такою, що
є такою, що  , тобто підінтегральний вираз містить складену функцію
, тобто підінтегральний вираз містить складену функцію  та диференціал
та диференціал  Тоді робиться заміна змінної (підстановка)
Тоді робиться заміна змінної (підстановка) 
 .
. неперервні і область значень функції
неперервні і область значень функції  збігається з областю визначення функції
збігається з областю визначення функції 
 явно виражається через нову змінну
явно виражається через нову змінну  . Зробимо в інтегралі
. Зробимо в інтегралі  , де
, де  - неперервно диференційовна функція, така, що її область значень збігається з областю визначення функції
- неперервно диференційовна функція, така, що її область значень збігається з областю визначення функції  . Тоді
. Тоді  і правильною є формула
і правильною є формула .
. функції
функції  знайти було б нескладно. У результаті остаточно отримаємо
знайти було б нескладно. У результаті остаточно отримаємо
 ,
, є розв’язком рівняння
є розв’язком рівняння  ;
; ;
; ;
; ;
; ;
; .
. ; 2)
; 2) 
 .
.

 . Тоді
. Тоді ;
; ,
,  .
. ,
,  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.
 . Отже,
. Отже, ;
;

 ;
;


 ;
;

 ;
; ;
;