 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Взаимно перпендикулярные колебания
Частица одновременно совершает колебания
Интерес представляет траекторию движения частицы, т.е. кривая, которую можно задать
в общем случае траектория представляет сложную кривую, которая называется фигурой Лиссажу. Рассмотрим случай колебаний с одинаковыми частотами
В общем случае зависимость
Проанализируем несколько случаев
Ангармонические (негармонические) колебания. Дифференциальные уравнения полученные ранее, справедливы при выполнении условия малости колебаний. При этом решения уравнений оказываются гармоническими.
Рассмотрим математический маятник, для которого нельзя использовать условие малости отклонений от положения равновесия.
Это нелинейное дифференциальное уравнение. Запишем
Подставим
Это дифференциальное уравнение ангармонических колебаний. Решение не является гармонической функцией и имеет вид:
Если
Свободные затухающие колебания. Пусть пружинный маятник совершает колебание в вязкой среде, где на него действует сила сопротивления среды
где
Второй закон Ньютона для грузика
Проецируем на ось
Обозначим
Это дифференциальное уравнение свободных затухающих колебаний. Здесь:
Решение уравнения имеет вид
Обозначим
Величина Величина Периодом затухающих колебаний называется величина
Энергия затухающих колебаний. Полная энергия маятника равна
Обозначим
Затухание колебаний считается малым, если выполняется условие
При этом очевидно, что
Здесь
Характеристики затухающих колебаний. Запишем:
Обозначим
Положим:
Время за которая амплитуда колебаний уменьшится в
Логарифмическим декрементом колебаний называется величина
Запишем:
где Добротность называется величина
Ограничимся малым затуханием.
Поиск по сайту: |

 ,
, .
. .
. 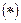
 ,
, ,
, 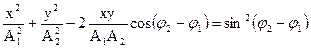 .
.
 .
.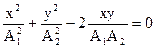 ,
,  ,
, ,
,  .
.
 .
. ,
, 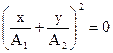 ,
, ,
,  .
.
 .
. .
.
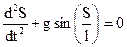 ,
, ,
,  ,
, ,
, ,
, 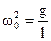 .
. в виде ряда
в виде ряда .
. 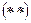
 ,
, .
. ,
, - амплитуда,
- амплитуда, - безразмерный параметр,
- безразмерный параметр, - круговая частота.
- круговая частота. , то
, то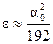 .
.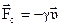 ,
,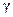 - коэффициент сопротивления среды,
- коэффициент сопротивления среды, - скорость грузика.
- скорость грузика.
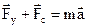 .
.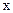
 ,
, .
.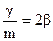 ,
, ,
, ,
, .
. - собственная круговая частота маятника.
- собственная круговая частота маятника.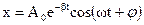 ,
, ,
, .
.
 .
.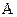 есть амплитуда затухающих колебаний.
есть амплитуда затухающих колебаний.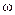 есть круговая частота затухающих колебаний.
есть круговая частота затухающих колебаний. ,
, .
. ,
, ,
, ,
,  ,
,
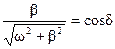 ,
,  ,
,  ,
, ,
,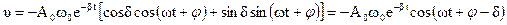 ,
, ,
, ,
,  ,
, ,
, ,
,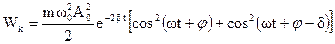 .
.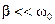 ,
,  .
. ,
, ,
, 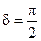 ,
, ,
, ,
,  ,
,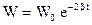 ,
, 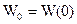 .
. .
. ,
, 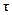 - время,
- время, .
. ,
, ,
,  .
.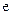 раз называется временем релаксации
раз называется временем релаксации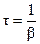 .
. ,
, ,
, .
.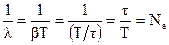 ,
, - число колебаний, за которое амплитуда колебаний уменьшается в
- число колебаний, за которое амплитуда колебаний уменьшается в 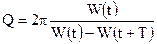 ,
, .
. ,
,  ,
, ,
, ,
,  .
.