 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сложение двух колебаний с незначительно отличающимися частотами
Пусть колебания происходят вдоль оси Х с одинаковыми амплитудами А1=А2=А и начальные фазы колебаний равны нулю.
причем Сложение произведем аналитически.
По формуле для суммы косинусов преобразуем последнее выражение
Очевидно, что первый сомножитель изменяется со временем медленнее второго. Следовательно, можно считать, что этот сомножитель есть амплитуда результирующего колебания А(t), изменяющаяся со временем по периодическому закону. Учитывая, что где То есть, результирующее колебание можно рассматривать как гармоническое с частотой Такие колебания с периодически изменяющейся амплитудой называются биениями. Частота колебаний амплитуды или частота биений равна разности частот складываемых колебаний, а период биений равен
График результирующего колебания (биений) показан на рис. 5.7.
5.5. Сложение взаимно перпендикулярных гармонических колебаний. Фигуры Лиссажу.
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях вдоль осей X и Y:
Уравнение траектории движения точки, участвующей одновременно в обоих этих колебаниях, находится исключением из уравнений параметра t. Рассмотрим частные случаи. I. Линейно поляризованные колебания: а) Пусть разность фаз складываемых колебаний
Деля второе уравнение на первое, получим уравнение траектории результирующего движения:
Результирующее движение - гармоническое колебание вдоль новой оси с амплитудой
б) Пусть - разность фаз
т.к. Деля последнее уравнение на первое, имеем:
Точка осуществляет движение вдоль новой оси (рис.5.9) по закону
II. Эллиптически поляризованные колебания: При произвольной разности фаз складываемых колебаний уравнения можно записать в виде:
После не очень сложных преобразований получим уравнение эллипса:
Это эллиптически поляризованные колебания.
При сложении взаимно перпендикулярных колебаний (гармонических) с кратными частотами результирующее движение будет происходить по сложным траекториям, которые называются фигурами Лиссажу. Вид этих кривых зависит от соотношения частот и разности фаз складываемых колебаний. На рисунке представлены фигуры Лиссажу для различных соотношений частот и разностей фаз
Поиск по сайту: |


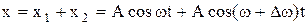 .
.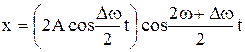 . (5.4.3)
. (5.4.3)
 . (5.4.4)
. (5.4.4) , амплитуда которого изменяется со временем согласно уравнения (5.4.4)
, амплитуда которого изменяется со временем согласно уравнения (5.4.4)

 ,
, .
. , т.е.
, т.е.
 .
. Траектория - прямая (см. рис.5.8 )
Траектория - прямая (см. рис.5.8 )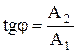
 и частотой
и частотой  описываемое уравнением:
описываемое уравнением: 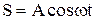 .
. .
. Тогда
Тогда  ,
,

 .
. .
.
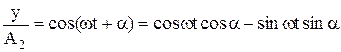 .
. .
. (рис.5.10):
(рис.5.10):



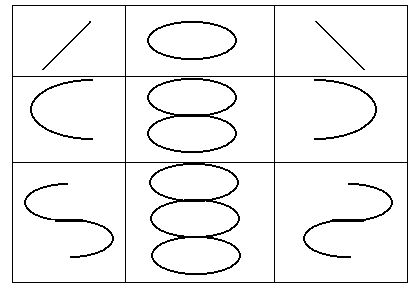 Рис.5.10.
Рис.5.10.

