|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Элементы статистики Ферми-Дирака на примере электронов проводимости в металлах. Электропроводность металлов ⇐ ПредыдущаяСтр 10 из 10
Вероятность нахождения электрона на том или ином энергетическом уровне дается распределением Ферми – Дирака:
где k – постоянная Больцмана; T – абсолютная температура; EF – энергия, называемая уровнем Ферми. Энергия уровня Ферми EF соответствует такому энергетическому уровню, вероятность заполнения которого равна 1/2. Рассмотрим вид функции Ферми-Дирака при температуре, стремящейся к абсолютному нулю. Как нетрудно видеть из формулы, для любой энергии частицы, большей энергии Ферми, экспонента в знаменателе стремится к бесконечности при , следовательно f(Е) стремится к нулю. Это значит, что все энергетические состояния с Е > EF совершенно свободны при абсолютном нуле. Если Е < EF при , f(E) стремится к единице. Это значит, что все квантовые состояния с энергией, меньше энергии Ферми, полностью заняты электронами. Отсюда понятен физический смысл энергии Ферми как параметра распределения электронов по состояниям: энергия Ферми есть максимально возможная энергия электронов в металле при температуре абсолютного нуля. Энергетический уровень, соответствующий энергии Ферми, называется уровнем Ферми.Если Т>0К, то при энергии частицы, равной энергии Ферми, функция распределения Ферми-Дирака равна 1/2. Это значит, что при любой температуре, отличающейся от абсолютного нуля, уровень Ферми заполнен наполовину. Вид функции Ферми-Дирака для двух различных температур показан схематически на рисунке. Изменение характера распределения электронов по состояниям связано с тепловым возбуждением электронов. При этом часть электронов переходит в состояния с энергиями, большей энергии Ферми. Соответственно часть состояний ниже уровня Ферми оказывается свободной. В результате функция f(E) "размыта" вблизи энергии Ферми. Тепловому возбуждению подвергается незначительная часть электронов, находящихся вблизи уровня Ферми. Функция Ферми-Дирака заметно отличается от вида, который она имела при абсолютном нуле, лишь при . Величина "размытия" пропорциональна температуре. Чем выше температура, тем более существенному изменению подвергается функция распределения.
Рис. 8.2. Функция распределения Ферми-Дирака при Т>0K
Концентрация свободных электронов в металле при абсолютном ноле равняется n= g (E)-плотность электронных состояний g (E)=(4π/h3)·(2mn)3/2·E1/2 (8.3) где mn - масса электрона, Е - энергия
Откуда следует, что Ef=(h2/2m)·(3n/8π)2/3 (8.5) Энергия Ферми имеет чисто квантовую природу и обусловлена специфическими свойствами электронов как фермионов. Она не является энергией теплового движения и существует при абсолютном ноле.
Пример 8.1. Рассчитать энергию Ферми для натрия, если его плотность ρ=970 кг/м3, а молярная масса М=23·10-3 кг/моль. Решение. Поскольку металл одновалентный, будем полагать, что концентрация свободных электронов равна концентрации атомов, определяемой из условия: n=nат=Nат/V=(NА·m)/(V·M)= =(NА· ρ)/M, где NА- число Авогадро тогда Ef=(h2/2m)·(3n/8π)2/3= (h2/2m)·(3 NА· ρ /8π· M)2/3 Подставляя числовые данные в СИ получим Ef=4,9·10-19Дж=3,1эВ Пример 8.2.Оценить длину свободного пробега электронов проводимости в меди, считая ее одновалентной, а также концентрацию электронов, если дельная электропроводность меди σ=6,0·107См/м, плотность ρ=8,6·103 кг/м3 Решение. Квантовая теория, учитывающая вырожденный характер электронного газа, дает следующие выражения для удельной электропроводности и удельного сопротивления
где n-концентрация свободных электронов, е-заряд электрона, m-его масса, vф-скорость фермиевских электронов, не зависящая от температуры, l-средняя длина свободного пробега этих электронов. Выразим среднюю длину свободного пробега Поскольку медь одновалентна, концентрация электронов в ней приближенно совпадает с концентрацией атомов и определяется из условия:
Максимальной скоростью в металле обладают электроны, энергия которых совпадает с энергией Ферми. Определяем ее приравнивая Ef=mvf2/2 Ef=(h2/2m)·(3n/8π)2/3 отсюда
Подставляем числовые данные
8.2. Носители заряда в полупроводниках, проводимость полупроводников. При Т=0 К полупроводники – изоляторы, тока они не проводят. При нагревании кристалла энергия электронов увеличивается и часть из них перебрасывается из валентной зоны в свободную запрещенную зону, которая при этом становится частично заполненной. Тогда в валентной зоне появляются свободные места – «дырки», несущие положительный заряд. Дырки вместе с электронами могут быть носителями тока. При включении внешнего электрического поля начинается упорядоченное движение электронов против поля, дырок в направлении поля. Полная электропроводность полупроводника
σ = e( pμp + nμn ) (8.8) где p и n – концентрации дырок и электронов соответственно; μp и μn – подвижности дырок и электронов соответственно; е – заряд электрона. Для собственного полупроводника концентрации дырок и электронов равны p= n, поэтому удельная проводимость в этом случае
σ = e n (μp + μn ) (8.9)
Поскольку в полупроводниках функция распределения электронов по состояниям имеет тот же вид, что и в металлах, то энергия Ферми в полупроводниках имеет тот же физический смысл: энергия Ферми - это максимально допустимая энергия, ниже которой при нулевой абсолютной температуре все энергетические уровни заняты [f(E) = 1], а выше которой все уровни пусты [f(E) = 0]. Для полупроводников, у которых при абсолютном нуле валентная зона полностью заполнена, а зона проводимости совершенно свободна, функция распределения имеет разрыв. Следовательно, уровень Ферми в полупроводнике должен лежать при абсолютном нуле в запрещенной зоне. Для собственного полупроводника концентрации электронов и дырок равны (n = p), т.к. каждый электрон, покинувший валентную зону, создает одну дырку. Концентрация электронов в зоне проводимости равна
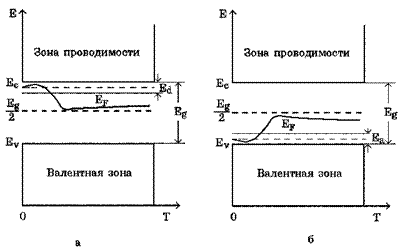
где здесь Аналогично можно вычислить концентрацию дырок в валентной зоне. где где Ev - энергия потолка валентной зоны, Приравнивая концентрации электронов и дырок, получим Разрешая последнее равенство относительно ЕF, получим Если эффективные массы электронов и дырок равны [ Температурная зависимость положения уровня Ферми в собственном полупроводнике определяется третьим слагаемым в уравнении. Если эффективная масса дырки в валентной зоне больше эффективной массы электрона в зоне проводимости, то уровень Ферми смещается с повышением температуры ближе к дну зоны проводимости. В противоположном случае уровень Ферми смещается к потолку валентной зоны. Положение уровня Ферми в примесных полупроводниках может быть найдено из условия электронейтральности кристалла. Для донорного полупроводника это условие записывается в виде здесь Nd - концентрация донорных уровней, nd - концентрация электронов на донорных уровнях. Концентрация электронов в зоне проводимости равна сумме концентраций дырок в валентной зоне и концентрации положительно заряженных ионов доноров (последняя, очевидно, равна Nd - nd). Концентрацию электронов на донорных уровнях можно вычислить, умножив концентрацию этих уровней Nd на функцию распределения Ферми-Дирака: где Еd - энергия активации донорных уровней. Подстановка в условие электронейтральности концентраций электронов и дырок, а также концентрации электронов на донорных уровнях приводит к следующему уравнению относительно положения уровня Ферми ЕF : При подстановке концентрации электронов на донорных уровнях в уравнение было сделано предположение, что газ электронов примесных атомов невырожденный, что позволило пренебречь единицей в знаменателе формулы. Это уравнение (ввиду его сложности обычно в общем виде не решают, а ограничиваются рассмотрением частных случаев. Например, при низких температурах, когда электроны в зоне проводимости появляются в основном за счет переходов с примесных уровней, а концентрация дырок близка к нулю, решение уравнения (8.18) имеет вид Из уравнения (8.19) следует, что при абсолютном нуле температуры энергия Ферми донорного полупроводника находится строго посередине между дном зоны проводимости и донорными уровнями. Температурная зависимость положения уровня Ферми определяется третьим членом в уравнении, который меняет знак с изменением температуры. Поэтому уровень Ферми с повышением температуры сначала смещается к зоне проводимости, а затем - к валентной зоне (рис. 8.3. а). Аналогично можно получить выражение для температурной зависимости уровня Ферми в акцепторном полупроводнике. График этой зависимости схематически приведен на рис. 8.3. б.
Рис. 8.3. Температурные зависимости положения уровня Ферми в донорном (а) и акцепторном (б) полупроводниках.
Пример 8.3. Определить положение уровня Ферми в Ge n-типа при Т = 300 К, если на 2·106 атомов Ge приходится один атом примеси (донорная). Концентрация атомов в Ge равна 4,4·1028 атомов/м3 (N). Постоянная G в выражении, связывающем число электронов в единице объёма в зоне проводимости с температурой и энергетическими уровнями, равна 4,83·1021 м–3·К–3/2 (Ge). Ширина запрещённой зоны Еg = 0,72 эВ, а расстояние между дном зоны проводимости и донорным уровнем 0,01 эВ. Решение. Концентрация электронов в зоне проводимости определяется выражением
где ЕF – энергия уровня Ферми; ЕС – энергия нижней границы зо- ны проводимости; k – постоянная Больцмана; Т – температура; NC – эффективная плотность состояний в зоне проводимости. В свою очередь,
где h – постоянная Планка; m* n– эффективная масса электрона; G – коэффициент пропорциональности. Перепишем выражение в виде
последнее и будем анализировать. Поскольку концентрация атомов в германии N = 4,4·1028 атомов/м3 и на 2·106 атомов германия приходится один атом примеси, а при температуре 300 К разница между донорными уровнями и дном зоны проводимости равна 0,01 эВ при Ез = 0,72 эВ, можно считать, что все атомы доноров будут ионизированы, тогда число свободных электронов в нём составит
Эффективная плотность состояний в зоне проводимости при 300 К из выражения Окончательно имеем
Таким образом, уровень Ферми находится ниже дна зоны проводимости на 0,18 эВ, что составляет 25 % от ширины запрещённой зоны. Пример 8.4. Удельное сопротивление чистого германия при некоторой температуре ρ=0,47 Ом м. Подвижности электронов и дырокравны соответственно μn=0,38м2/(В·с), μp=0,18м2/(В·с). Вычислить их концентрацию Решение. Электропроводность полупроводника связана с удельным сопротивлением следующим образом ρ= 1/σ Удельное сопротивление можно вычислить о приведенной выше формуле σ=σn+σp=|e| n (μn+μp) Тогда концентрация электронов и дырок Подставляем числовые значения и получаем n=2,3·1019 м-3 Пример 8.5. Удельное сопротивление собственного Ge при Т = 300 К ρ = 0,43 Ом·м. Подвижности электронов и дырок в Ge равны соответственно 0,39 и 0,19 м2/В·с. Определить собственную концентрацию электронов и дырок. Какова будет концентрация электронов и дырок при той же температуре, если Ge легироватьпримесью атомов сурьмы так, что один атом примеси приходится на 2·106 атомов Ge? Каково будет удельное сопротивление легированного Gе? Решение Удельная проводимость полупроводника σ определяется следующим образом: σ = e( pμp + nμn ) Для собственного полупроводника p = n, поэтому удельная проводимость в этом случае
Это и есть собственная концентрация носителей в Ge при 300 К. Если Ge легирован донорной примесью, то по условию концентрация донорных примесей
При температуре 300 К можно считать, что все атомы примеси ионизированы и nn = 2,2 ·1022 м−3 . Тогда концентрация дырок в Ge n-типа
Удельное сопротивление легированного полупроводника
так как первым слагаемым в скобках можно пренебречь.
Из анализа решения следует, что при такой степени легирования удельное сопротивление Ge уменьшилось практически на три порядка (собственное ρ = 0,43 Ом·м).
Поиск по сайту: |
 (8.1)
(8.1)
 (8.2)
(8.2) (8.4)
(8.4)
 (8.6)
(8.6) (8.7)
(8.7)
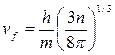 и
и 

 (8.10)
(8.10) - эффективная плотность состояний в зоне проводимости. (8.11)
- эффективная плотность состояний в зоне проводимости. (8.11) энергия дна зоны проводимости,
энергия дна зоны проводимости, 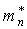 - эффективная масса электрона у дна зоны проводимости.
- эффективная масса электрона у дна зоны проводимости. (8.12)
(8.12) - эффективная плотность состояний в валентной зоне. (8.13)
- эффективная плотность состояний в валентной зоне. (8.13) - эффективная масса дырки
- эффективная масса дырки (8.14)
(8.14) (8.15)
(8.15)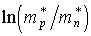 = 0] уровень Ферми собственного полупроводника при любой температуре располагается посередине запрещенной зоны.
= 0] уровень Ферми собственного полупроводника при любой температуре располагается посередине запрещенной зоны. , (8.16)
, (8.16) (8.17)
(8.17)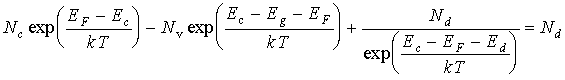 (8.18)
(8.18)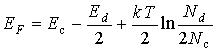 . (8.19)
. (8.19)