|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Экспериментальная часть. Задания по работе
Задания по работе 1. Изучить теоретическую часть работы. 2. Реализовать компьютерную программу, принимающую на выход изображение и выполняющую преобразование дисторсии. 3. Провести апробацию реализованной программы на различных изображениях. Теоретическая часть Дисторсия (рис. 1) возникает в результате смещения относительно своего идеального положения точек, лучи от которых идут под небольшим наклоном к оптической оси системы. Эта аберрация наблюдается как сжатие изображения к центру (подушкообразная дисторсия) или расплывание от центра (бочкообразная дисторсия). Дисторсия может возникать даже в случае устранения всех рассмотренных видов аберраций.
Рис. 1.Результат дисторсии. Нормальное изображение, подушкообразная дисторсия, бочкообразная дисторсия Рассмотрим процесс формирования изображения в идеальной оптической системе. Пусть расположение каждой точки в плоскости, перпендикулярной оптической оси задается вектором В изображении, сформированном в идеальной оптической системе, положение каждой точки может быть описано вектором
где
где Дисторсия выше третьего порядка на практике наблюдается редко, поэтому часто для коррекции достаточно использовать формулу
Если в оптической системе присутствуют другие виды аберраций, то выражение для вектора Дисторсия на цифровых изображениях может быть скорректирована программными средствами. Наиболее простой способ коррекции дисторсии – это применение к искаженному изображению преобразования дисторсии с противоположным знаком. При известных параметрах оптической системы, формирующей искаженные изображения можно точно рассчитать параметры обратного преобразования, однако зачастую такая информация отсутствует. В этом случае приходится осуществлять ручной или эвристический подбор корректирующего коэффициента дисторсии. Экспериментальная часть Функция дисторсии, реализованная на языке MATLAB. function[res] = distortion(img, f3, f5, inc) % distortion - функция, реализующая дисторсию пятого порядка % для изображения img с коэффициентами дисторсии f3, f5 % и коэффициентом увеличения inc [height, width] = size(img); h2 = height/2; w2 = width/2; rs = h2^2 + w2^2; rheight = h2 * inc + f3 * rs * h2 + f5 * rs^2 * h2; rwidth = w2 * inc + f3 * rs * w2 + f5 * rs^2 * w2;
for i = 1 : height for j = 1 : width ic = i - height/2; jc = j - width/2; rn = ic^2 + jc^2; id = ceil(inc * ic + f3 * rn * ic + f5 * rn^2 * ic + rheight); jd = ceil(inc * jc + f3 * rn * jc + f5 * rn^2 * jc + rwidth); res(id, jd) = img(i, j); end; end; end
Результаты работы функции для дисторсии третьего порядка Коэффициенты подушкообразной дисторсии: Коэффициенты бочкообразной дисторсии:
а) б) в) Рис. 2. а) исходное изображение; б) изображение, искажённое подушкообразной дисторсией; в) изображение, восстановленное бочкообразной дисторсией. Результаты работы функции для дисторсии пятого порядка Коэффициенты подушкообразной дисторсии: Коэффициенты бочкообразной дисторсии:
а) б) в) Рис. 3. а) исходное изображение; б) изображение, искажённое подушкообразной дисторсией; в) изображение, восстановленное бочкообразной дисторсией.
Поиск по сайту: |

 , где x и y – пространственные координаты в этой плоскости.
, где x и y – пространственные координаты в этой плоскости.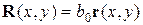 ,
, – коэффициент оптического увеличения. Эффект дисторсии заключается в неправильном относительно идеального расположении точек на изображении. Причем в случае дисторсии координаты вектора
– коэффициент оптического увеличения. Эффект дисторсии заключается в неправильном относительно идеального расположении точек на изображении. Причем в случае дисторсии координаты вектора  зависят только от удаленности точки от оптической оси и коэффициентов дисторсии
зависят только от удаленности точки от оптической оси и коэффициентов дисторсии ,
, ,
,  ,
, 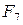 , … – коэффициенты дисторсии различных порядков,
, … – коэффициенты дисторсии различных порядков,  – длина вектора
– длина вектора  .
.